Math Game: 두 판 사이의 차이
(→행렬 만들기) |
(차이 없음)
|
2008년 10월 23일 (목) 17:47 기준 최신판
속도전
- 암산, 수를 키워가면서 -> 점점 의미있는 수로
- 10초 ~ 20초 팻말( 4 자리 수가 써있는 )이 지나가는 동안, 그 수로 100 만들기 : 4대 연산, 7 대 연산 ...
번갈아가면서
- - 가정 : A 가 먼저하는 사람이라 하자.
- - 기왕이면 '필승 전략'이 찾아보자.
15 만들기
- 준비물 : 1 부터 9 까지 써있는 종이 쪽지 (카드)
- A 가 하나를 빼고 B 가 남은 것 중 하나씩 뺀다.
- 먼저 세장을 모아 15를 만들 사람이 승리
행렬 만들기
- 준비물 : 3 * 3 표.
- 두 사람이 1 ~ 9 에서 하나씩 골라 적는다.
- 표가 다 채워졌을 때, determinant 를 구해서 양수면 A 가, 음수면 B 가 이긴다.[1]
5의 배수 만들기
- 두 사람이 1 ~ 27 까지 한번씩 써 있는 수의 열에서 하나씩 빼내간다.
- 두 개만 남았을 때, 그 합의 5의 배수면 A 가, 아니면 B 가 이긴다.
55 만들기
- 1 ~ 101 까지 써있는 카드에서 원하는 것 9 개를 지운다.
- B 도 남은 것 중 9 개씩 지운다.
- 11번 하고 나면 숫자 2 개 남는다.
- 두 수의 차이가 55 면 A 가 이기고, 아니면 B 가 이긴다.
100 먼저 만들기
- A 가 100 보다 작은 어떤 수를 댄다.
- B 는 A 가 부른 수보다 큰 수를 댄다. 차이는 10 보다 작거나 같아야 한다.
- 먼저 '백' 을 말하는 사람이 이긴다.
- 여기서 수는 100 대신 50, 차이는 10대신 7 로 해도 상관없다.
- 문제를 바꾸어 100 이 들어가는 수를 먼저 말한 사람이 지는 게임을 해도 된다.
NOTE
- ↑ Determinants of 3-by-3 matrices
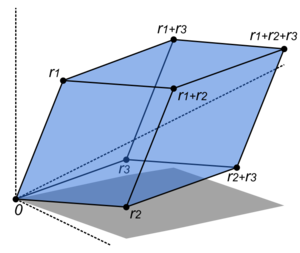
The volume of this Parallelepiped is the absolute value of the determinant of the matrix formed by the rows r1, r2, and r3.
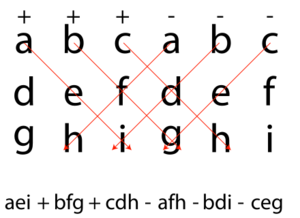
The determinant of a 3x3 matrix can be calculated by its diagonals. which can be remembered as the sum of the products of three diagonal north-west to south-east lines of matrix elements, minus the sum of the products of three diagonal south-west to north-east lines of elements when the copies of the first two columns of the matrix are written beside it as below:
Note that this mnemonic does not carry over into higher dimensions.


