Pf Circle Separation Intersectin

원의 정의 에서

네 점에 대해 서로 교차함과 서로 떼놓음 관계의 등가성 보이기

ACBD순서

ADBC순서

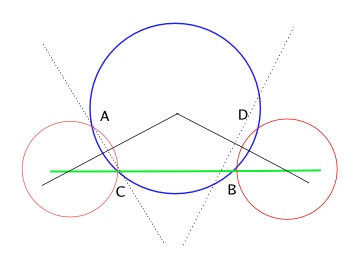
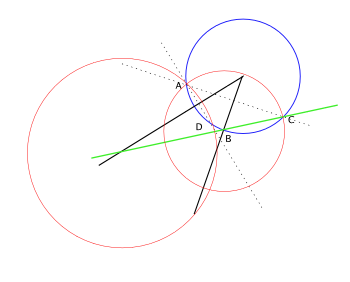
이것을 분명하게 보이기 위해서는 아래 두 사실을 보이면 된다.

1. $AC\ \|\ BD\ \Rightarrow \ AC*BD$ : A, C 를 지나 B, C를 지나는 원이 최소한 두 점에서 교차하면, A,C는 B, D와 서로 떼어놓는다.
2. $AC\ \|\ BD\ \Leftarrow \ AC*BD$  : 서로 떼어놓지 않으면 A, C 를 지나 B, C를 지나는 원이 교차하지 않도록 두 원을 작도할 수 있다.

첫번째 사실은 이미 우리가 도입부에서 본 정리를 환기하면 충분하다. A, C 를 지나 B, C를 지나는 원이 최소한 두 점에서 교차하면, 이 네 점은 어떤 직선이나 원 위에 있게 된다. 그리고 앞의 두 원이 최소한 두 점에서 교차하기 위해서는 두 점 A 와 C 사이에 B 또는 D 가 하나만 있게 된다.

두번째 사실은 서로 떼어놓지 않은 관계에 있는 두 묶음일 때, 교차하지 않은 두 원, 하나는 A, C를 지나고 다른 하나는 B, D를 지나는 원을 작도하는 방법을 보이면 된다. 이 경우는 다시 A, C, B, D 가 한 직선에 있는 경우와 한 원에 있는 경우로 나눠서 볼 수 있다.

• 직선에 있을 때(collinear)는 A, C를 지름으로 하는 원을 하나, B,D를 지름으로 하는 원을 하나 작도한다.
• 원에 있을 때(concyclic)는, 다시 두가지 경우가 가능하다. 어떤 방향으로건 방향을 정했다고 하면, (직접 작도해보라)
  • A, B, D, C 순서인 경우, 다시말해 $AB\ \|\ CD$ 가 아닌 경우.
  • A, D, B, C 순서인 경우, 다시말해 $AB\ \|\ CD$ 인 경우. 이 경우는 다시 두 경우로 나뉜다.
    • BC = AC 가 아닌 경우
    • BC = AD 인 경우

원의 정의 로 돌아가기.