No Repeat sequence: 두 판 사이의 차이
(차이 없음)
|
2008년 3월 29일 (토) 23:28 기준 최신판
같은 단어를 반복해서 쓰는 경우가 우리말엔 꽤 있다. '빨리빨리' '하나하나' '졸졸졸' '꿀꺽꿀꺽' ... 단어 하나가 반복한 경우도 있고, 하나로 쓸 수 있는 말이라도 두 번 되풀이해서 강조하기도 한다. 세계의 언어 중에는 우리 한글처럼 반복을 통해 '강조'나 '복수형'을 나타내는 언어들이 있다. 영어는 그렇지 않은 언어에 속한다. 하지만, 어떤 민족의 언어도 컴퓨터만큼 반복을 많이 해서 글자를 나타내지는 않을 것이다. 2진 체계(binary)로 나타낼 경우, 미국 표준 코드 체계 ASCII[1]를 컴퓨터 안의 기계들이 이해하는 말로 바꾸는 예를 보자.
- '다섯'은 컴퓨터 기본 언어인 ASCII 로 쓸 때, 우리에게 익숙한 형태인 5 로 쓴다. 그것을 컴퓨터 2 진 체계 언어로 쓰면 00110101 다.
- 0011000100110000 를 ASCII 언어로 바꾸면 10이다.
- ASCII로 'love' 를 2진 언어로 번역하면 01101100011011110111011001100101 이다.[2]
- 'mathematics' 도 바꾸어 보았다. 길다. m은 01101101 다. ma 는 01101101 01100001 이고,
- 0110110101100001011101000110100001100101011011010110000101110100011010010110001101110011
어떻게 그렇게 바꿀 수 있는거지? 000110110111011101111 이라는 글자로 아무렇게나 표현했다면 사람의 언어로 어떻게 바뀔까? 궁금해할지 모른다. 그리고 생각이 멀리멀리 날아다니는 사람은, 사랑이 무얼까? 수학이란 무엇인가? 문제들까지 던지고 있을지 모르겠다.
지금부터 우리가 함께 보고자 하는 건 그런 식의 '내용적'인 부분이 아니다. 기호 자체에만 집중하자. 관심을 집중하려는 주제는 바로 문자열에 반복 부분이 있는가 없는가? 없게 하려면 얼마나 길게 될까?다. 더 자세히 말하면
- 알파벳이 2개만 있는 2진 체계로 반복 없는 문자열을 만든다면 최대 몇 개일까?
- 알파벳이 3개있는 3진 체계라면? 16진 체계라면?
- 반복 없는 문자열은 끝없이 길어질 수 있을까? 이와 같은 문제들이다.
이런 문제들을 무엇하러 탐구할까? 이런 쓸 데 없는 생각보다 더 실용적이고 중요한 문제를 해결해야하지 않을까? 라고 생각할 수도 있겠다. 물론 당장 쓰임새가 있도록 탐구하는 것도 중요하다. 하지만, 수학은 순수하다. 호기심으로 시작했는데, 상상의 나래를 널리 펼치고 세월이 흐르면서 예기치 않은 데서 놀라운 힘을 발휘한 경우가 자주 있었다. 이 문제도 그렇다. 여러분의 손전화기, 컴퓨터, 암호 전송, 지구와 달거리 측정이 위의 문제들과 연관이 있다면 믿어지나?
문제 속으로 들어가 흠뻑 젖어들기 전에 부탁이 하나 있다. 읽다보면 점으로된 네모 상자 안에 질문을 만날 것이다. 그러면, 그 다음으로 넘어가지 말고 잠시 멈추어라. 스스로 이런저런 생각을 해보고, 가능하면 직접 답을 내보기 바란다. 앞에서 던졌던 문제들을 풀어가는데 어떤 공식도 필요 없다. 집중과 끈기와 차근차근 따져보는 마음만 있으면 탐험의 준비는 다 된 셈이다. 자, 그럼, 준비는 다 되었다. 이제 흥미진진 문제 속으로 !
문제 다듬기
문제를 잘 풀기 위해 가장 먼저 할 일은 문제를 말끔하게 정돈해서 내놓는 것이다. 같은 문제의 내용을 담고 있어도 복잡하게 표현되어 있으면 이해도 어렵고 풀기도 어려울 수 있지만, 명료하고 이쁘게 할 수 있으면 그렇게 하는 것이 문제를 잘 풀고 새로운 문제로 발전시키는데 매우 중요하다. 앞에 던졌던 문제를 간단하게 다시 써보기로 하자. 집중할 문제는 바로 이렇다.
|
알파벳이 n 개 일 때, m 개의 단어들로 문자열을 쪼갰을 때, 어떤 단어도 반복해서 나오지 않을 가장 긴 문자열 k 는 ? |
우선 가장 간단한 경우, n 이 2 인 경우를 보자. 앞의 2진 체계일 때다. 0과 1을 쓰는 대신, 여기에 쓰기 편하게 하고, 현실적인 느낌이 조금이나마 더 들도록 a, b 로 쓰겠다. 그렇다면 앞의 5를 보자. aabbabab 로 쓸 수 있을 것이다. 여기서 반복 부분은 있나? 있다면 무엇인가? 아래 문자열에는 반복하는 단어가 있나?
그렇다. 반복 부분은 있다. 있기만 한게 아니라 많다. a 다음에 바로 a 가 나와서 반복이고, a 에 b 도 반복이다. 그리고 두 글자로 한단어를 이룬다고 가정할 경우 ba 도, ab 도 반복한다. 세 글자로 단어를 이룬다고 할 때도 반복이 있을까? 앞의 문자열에 있는 세 글자 단어(문제에서 m 이 3인 경우)는
여기도 반복하는 단어가 있다. bab 다. 다음 문제에 답을 해보라.
- 앞 문자열에서 네 단어 단위로 볼 때도 반복하는 단어가 있을까?
- 앞의 예에서 10을 2진 체계로 바꾼 문자열에서 n 이, 2 일때, 3일 때, 4일 때, 5 일때를 검사해보라.
- love 는 어떨까? '사랑'에는, 한 말 또 하고 한 말 또 하는 동어반복이 많이 있을까?
문자열의 길이가 k 라면 단어 길이가 2일 때, 3일 때, 4일 때 , ... , k-1 개 까지 가능한 모든 경우를 검토해야할 것이다. a와 b 두 문자만 알파벳(n)으로 하는 을 만든다고 하고, 그 중 어떤 문자열의 길이(k)가 8 이라 하자. 거기에 길이(n) 2인 단어는 일곱 개, 길이가 3인 단어는 여섯 개, ... , 길이가 7 인 단어는 두 개, 길이가 8인 단어는 하나다. 물론 이때 단어 길이가 8 이면 반복은 없다.
- 길이 8 인 문자열에 반복하는 단어가 있는지 검토하려면 모두 몇 번 검사해봐야 할까? (단어 길이가 1인 경우는 제외한다.)
- 길이 100 인 문자열에 반복하는 단어가 있는지 검토하려면 모두 몇 번 검사해봐야 할까? (단어 길이가 1인 경우는 제외한다.)
이미 눈치를 챘겠지만, 문자열의 길이가 길어질수록 반복하는 단어가 있는지 없는지 검토하는 것은 엄청나게 힘들어진다.
알파벳은 둘 뿐이고, 단어 길이 2인 경우 : n이 2고, m이 2인 경우
다시, 처음 던졌던 문제로 돌아가자.
|
a, b 두 알파벳만 있다. 그 때, 길이 2인 단어만으로 문자열을 만든다면, 반복 구간이 없는 문자열은 길어야 얼마까지일까? |
단어 길이가 2인 경우는, 일일이 확인해봐도 어렵지 않다. a 로 시작한다고 해보자.
- a 에서 다음 문자가 a 라고 해보자. 다시 말해 aa 다. 그 다음에는 a 가 오면 안된다. aa 가 반복하게 되니까. 그래서 그 다음은 aab 가 될 것이고, 여기서는 a , b 를 모두 붙일 수 있다. b 를 붙여나간다고 해보자. aabb 다음은 b 가 오면 안된다. 그래서 aabba가 될 것이다. 그 다음은? a 를 붙여도 b 를 붙여도 모두 반복구간이 나올 수 밖에 없다. 그 길을 선택한 경우 길이는 최대 길이는 5다.
그런데 과연 이것이 가장 길까? a 부터 시작않고 달리 한다면 더 긴 것이 있지 않을까? 그렇지 않다. 아래 그림처럼 가능한 모든 경우를 해볼 수있다. (그림에서는 a 로 시작한 경우만 보았다. 이 때, 두 개가 최대문자열이다. b 일 때도 같은 방식으로 검토하면 최대 문자열은 두 개 나온다.)
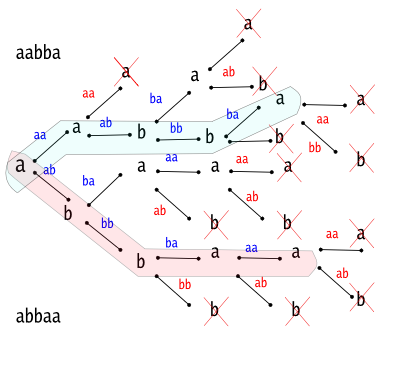
따라서 가능한 최대 길이를 갖는 문자열은
넷으로 모두 길이(k)는 5다. 그런데 이것을 그림처럼 일일이 해보는 것은 간단한 일이 아니고, 상상력을 발휘하는 것도 없고, 논리적인 추측도 없다. 따라서 덜 수학적이다. 심하게 말하면 전혀 수학적이지 않다.
알파벳이 둘만 있는 경우, 단어 길이 2로 반복없는 최대 문자열은 5가 될 수 밖에 없다는 것을 확인하기 위해서 일일이 해봐야 하는 것은 아니다. 논리적으로 따져봐도 충분히 가능하다.
- a, b 둘로 만들 수 있는 길이 2인 단어의 유형은 aa, ab, ba, bb 넷 밖에 없다. 반복 없이 최대 길이로 된 문자열을 만들기 위해서는 이것들이 모두, 한번씩만 나와야 한다. 이어 쓰면 여덟의 문자열이 되지만, 중간에 세 번 겹쳐 쓸 수밖에 없기 때문에 반복없는 문자열은 5 일 수 밖에 없다.
또는 이렇게 말해도 된다.
- a, b 둘로 만들 수 있는 길이 2인 단어의 유형은 aa, ab, ba, bb 넷 밖에 없다. 그런데 길이 6의 문자열에는 길이 2인 단어가 다섯 나온다. 그래서 겹치는 것이 나올 수 밖에 없다. 따라서 반복 하는 단어가 없는 문자열의 최대 길이는 5 다.
하나를 알면 새롭게 모르는 것이 여럿 튀어나오곤 한다. 문제를 하나 풀고 났더니 호기심이 더 발동하고, 물음표는 늘어난다.
- 최대 길이를 갖는 문자열이 넷만 나오는데 왜 그럴 수 밖에 없을까?
- 최대 길이를 갖는 문자열 네 경우에 어떤 규칙이 있지 않을까?
다행히 이 질문들은 하나의 답만 찾으면 끝이 난다. 가만히 들여다보면서 규칙을 찾아보라. 그리고 그 규칙이 그럴 수 밖에 없는 것인지, 우연적인 것인지 파악해보자. 만약 그럴 수 밖에 없는 이유가 있다면 단어길이가 3 으로, 4로 늘어나도 보다 일반적인 경우에 대해서도 적용해 볼 수 있다. 다시 말해, 알파벳이 a ,b 둘 밖에 없는 경우, 단어 길이 3 이나, 4, 5, ... 에 대해서도 같은 논리를 적용해볼 수 있다. 문제를 명료하게 해보자.
|
앞의 최대 문자열 네가지 결과를 보고, 규칙을 발견해보라. 그럴 수 밖에 없었는가 ? |
혹시 어떤 규칙을 발견했는지? 그리고 그 중에 필연적인 것이 있었는지? 한가지 분명한 것은 바로, a 로 시작한 것은 a 로 끝이 났고, b 로 시작한 것은 b 로 끝났다는 것이다. 그렇다고 이것이 a 로 시작한 문자열이 a 로 끝나면 모두 반복없는 최대 문자열이 된다는 것은 물론 아니다. aaa 나, aabaa만 봐도 그렇다. 그렇다면 무엇을 말하고 있을까? 다름 아닌,
- 최대 문자열이면, a로 끝났을 때, 시작은 a 일 수밖에 없다
이다. 그럴 수 밖에 없다.왜 그럴까? (멈추고 생각해보라.) 아래와 같이 누군가 답을 했다고 하자.
- a 로 끝이 났는데, a로 시작을 안했다고 해보자. 그말은 ab, aa 로 시작을 안했다는 말이다. 그렇다면 시작이 아닌 중간 어딘가에 ab 와 aa 가 나타났을 것이다. aa 가 나타났을 때는 길이 2인 단어 aa 가 반복하지 않기 위해 baa 만 가능하다. ab가 나와야 할 때는 aab 또는 bab 가 가능하다. 이 중 bab 는 불가능하다. 이미 앞에서 ba 가 나왔으니까. 다시 말하면, baa, aab 가 앞에서 나왔다는 것을 뜻한다. 여기에 있는 단어 중 a 로 끝나고 길이 2인 단어는 이미 ba, aa 모두 있다. 그래서 최대문자열의 끝에 a 가 올 수 없다. 왜냐하면 끝은 a 로 끝나서, 가능한 단어는 (우리의 알파벳은 a, b 두 개뿐이므로) aa, ba 뿐이다. 어느 경우건 이미 중간에 나온 단어와 겹친다. 그래서 시작이 a 였을 수 밖에 없다. 끝이 b 인 경우에 대해서도 마찬가지다.
논리적으로 맞는 말인가? 여러분 중 달리 생각하거나, 위와 다른 이유를 생각해본 사람은 없나? 자기 생각을 공책에 적어보자. 그리고 위의 문제가 풀리면 길이가 5인 반복 단어 없는 최대문자열은 넷 뿐이라는 사실을 받아들일 수 있는가? 만약, "아니야!" 라고 한다면 왜 그렇게 생각하나? 만약, "그래!" 라고 했다면 왜 그렇게 생각했나?
아직 답을 못했다고 실망할 필요는 없다. 더 생각해보거나, 이 글을 읽어가다보면 아래 단어 길이가 3일때처럼 조금 더 복잡한 경우를 다룰 때 이해할 수 있을 것이다. 그렇다면, 단어 길이가 3이면 어떨까? 우리가 방금 본 것과 같은 '비슷한' 논리가 3인 경우에도 과연 성립할까?
알파벳은 둘 뿐이고, 단어 길이 3인 경우 : n이 2고, m이 3인 경우
이미 단어 길이 m 이 2인 경우를 보았는데,이제 단어 길이가 3인 경우를 보자. 앞에서 푸는 과정에서 단어 길이가 결정적으로 영향을 준 것이 어느 부분인지 관심을 가지고 다시 보라. 유심히 들여다보라. 과연 어디서 단어 길이가 중요한 역할을 했던가? 문제들을 다시 정리해보면서 찬찬히 발을 담궈가자.
|
풀이 과정에서 단어 길이가 영향을 준 부분은 분명하다. 단어 길이가 3이므로, 이제 서로 다른 단어들은 여덟 개다.
따라서 단어의 반복이 없는 문자열의 최대길이를 찾는 것은 어렵지 않은 일이다. (몇 개일까? 스스로 답해보라.)
그렇다. 반복이 없어야 하니까, 여덟 단어는 한번 씩만 나와야 하고, 그것들은 둘씩 겹치면서 나온다. 또는 이렇게 말해도 된다. 두 글자씩 겹치면서 길이가 3인 단어를 만들어보자. 그런 식으로 11개 길이 문자열에서는 길이 3인 단어들이 9개 나온다. 11개 일 때는 반복하는 단어가 있을 수밖에 없다. 따라서 반복 단어 없는 문자열의 최대길이는 10이다. 앞에서 단어 길이가 2 일 때 한 것처럼 그림을 직접 그려서 알아보는 것은 매우 까다로와진다는 것을 잊지 말아라.단어길이가 2일 때의 그림처럼, 가지를 뻗어가는 방식으로 시도해보라. [3])
그렇다면 두번째 질문, 규칙은 무엇일까? 우리가 앞에서 규칙을 발견하고 앞에서 그것이 그럴 수 밖에 없다는 것을 보일 때, 단어의 길이가 결정적인 역할을 했는지 보자. (스스로 실제로 다시 확인해보고 다음으로 넘어가자.)
단어 길이가 2일 때 해명한 논리를 보면 단어 길이는 처음에만 역할을 했을뿐이다. 다른 아닌, 이번의 경우는 이렇게 바뀐다.
- 어떤 문자열이 3 길이 단어가 반복 없이 나오는 최대 문자열이라면, ab 로 끝난 것은 ab 로 시작할 수 밖에 없다.
그렇다면 아래 질문에 답해보라.
|
n 은 2, m 은 3 일 때, 최대 문자열은 몇 개가 가능할까? |
확인하는 뜻에서 답을 해보겠다. 맞는지 확인해보라. 물론 다른 논리로 답을 해도 된다. 어려분 나름대로 한 방식이 더 나은 답일 수도 있다.더 나은 답이 아니라도 여러분 자신을 위해서는 더 낫다.
- ab 로 끝난 것은 ab 로 시작했을 수밖에 없다. 왜냐? ab 로 끝이 났는데 ab 로 시작을 안했다면 어떻게 될까? 우리가 보는 단어는 길이 3이다. 그래서 ab 로 시작 안했으면 aba 또는 abb 로도 시작 안했다. 따라서 분명 시작이 아닌 중간 어딘가 aba 와 abb 들이 나온다. 그렇다면 aba 가 중간에 나왔다는 것은 aaba 또는 baba 가 나왔다는 말이다. aaba 가 나왔다고 해보자. 그렇다면 abb 가 나올때 가능한 aabb 또는 babb 중 처음 것은 불가능하다. aab 가 겹치기 때문이다. 그렇다면 aaba 와 babb 가 중간 어딘가에 있는 것이다. 그렇다면 ab로 끝날 수 있는 가능한 두 경우 bab, aab 가 이미 앞에서 모두 나왔다는 말이다. 따라서 말이 안된다. ab 가 아닌 다른 경우에 대해서도 마찬가지다. 직접 다른 경우에 대해서 보라.
앞의 논의는 굳이 ab 인 경우만 해당하는 것이 아니다. aa, ab, ba, bb 인 경우로 끝나는 것은 반드시, 차례대로, aa, ab, ba, bb로 시작해야 한다. 이렇게 될 수 있는 경우는 모두 몇 개일까? [4] 이 경우 가능한 최대 문자열은 아래와 같다.
그런데, 여기에 나온 것들은 혹시 어떤 규칙이 없나? 스스로 찾으면 좋겠다. 아니면, 아래 고리모양으로 표현하기 부분을 읽을 때 알 수 있을 것이다.
일반화 1
지금까지 n 이 2 일 때, 단어 길이가 2 인 경우와 3 인 경우를 보았다. 2인 경우, 단어 반복이 없는 최대 문자열은 4개가 있었고, 3인 경우는 8개가 있었다. 이것을 더 일반적인 경우로 확장하면 어떻게 될까? 다음 질문에 스스로 답을 해보라.
|
방금 전에 문제에 던졌던 질문에 대해 혹시 나름의 답을 했다면 아래의 결과와 견주어 보기 바란다.
- 4 글자 단어로 반복 없는 최대문자의 길이는 19, 가능한 최대 문자의 경우는 16개. 이렇게 되는 어떤 것도 앞의 세문자와 뒤의 세문자가 같다.
- 5 글자 단어로 반복 없는 최대문자의 길이는 36, 가능한 최대 문자의 경우는 32개. 이렇게 되는 어떤 것도 앞의 네문자와 뒤의 네문자가 같다.
- 100 글자 단어로 반복 없는 최대문자의 길이는 , 가능한 최대 문자의 경우는 개.
문제를 달리 보기
고리모양으로 나타내기
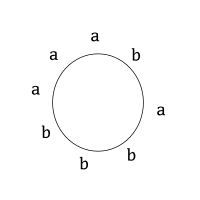
앞에서 단어의 길이가 3 일때 반복 없는 문자열을 만들기 위해 참여한 단어들은 모두 8개 였다. 그래서 이 '최대 문자열'을 나타내는 방법으로 가 단순하게는
로 쓸 수 있다. 거기에 참여한 단어들을 하나씩 나열한 방법이다. 하지만, 이것은 더 간단히 할 수 있다. 그리고 앞에 8 가지 경우 처럼, 아래와 같이 하나의 문자열로 쓸 수도 있었다.
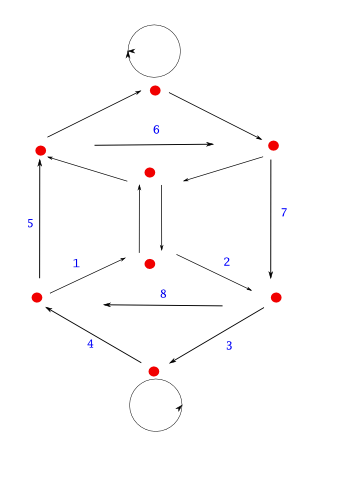
이 방법은 길이 10인 문자열로 간단히 나타낸 것이다. 모두 8개가 있다. 이 최대문자열들은 규칙이 있다. 돌려가면서 읽어보면 순서가 같다. 옆의 고리모양을 보라. 앞에서 가능한 8 가지 어떤 것이나 가능하다! 길이 10 자리 최대 문자열 8 개를 하나의 고리로 나타낸 것이다. 반복 단어 없는 최대 문자열을 나타내기 위해 다른 방법은 없을까? 앞에서 단어 길이가 3 일 때 최대 문자열이라면, 시작 두 글자와 끝 글자가 같았다는 것에 주목하라. 이 둘을 겹쳐 붙인다면, 어떤 것이든, 옆의 그림과 같이 줄여 쓸 수 있다. 8개 글자로 된 고리 하나면 충분하다.
도시와 길로 나타내기

이것을 고리로 나타내고 보니, 더 분명하게 드러나는 사실이 있다. 가능한 최대문자열 8개는 하나의 고리로 모두 나타낼 수 있는데, 아무 글자에서 시작하든, 방향을 고정하고 (시계 방향 또는 시계 반대 방향) 차례로 8글자를 적고, 처음 시작한 두 글자를 이어 쓰면 된다. 이것은 10문자로 나타내는 것과 일치한다. 이 방식으로 하면 '단어 반복없는 최대 문자열'을 하나의 체계로 볼 수 있게 된다. 더 분명해졌다.
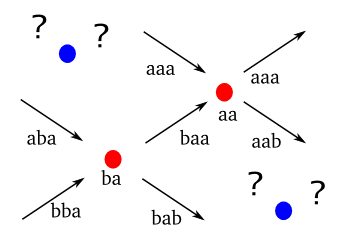
예를들어, ba가 나오는 것을 보자. 방향을 달리하면서 보다시피, ba 를 매개로 하여 만들어질 수 있는 글자는 넷이다. ba 앞에 a 또는 b 가 들어붙을 수 있고, ba 다음에 a 또는 b 가 들어불을 수 있다. 아래에 그림으로 나타내보았다.
그렇다면 이것은 해석하기에 따라, ba를 어떤 도시로 보고 aba, bba를 들어온 길, baa, bab 를 나가는 길로 볼 수도 있다. 이번엔 단어를 '길'로 해석한 것이다. (그렇게 해석을 하지 않고 달리 해석할 수도 있을 것이다. 상상의 나래를 펼쳐보라, 여러분 나름의 해석을 해보라.) 그렇다면, 이것을 조금 더 나탄내보기로하자.
하나의 도시를 나타내는 것은 매우 쉬운 일이었지만, 이렇듯 도시가 여럿일 경우는 '한번 더' 생각해야 한다. 어떻게 하는 것이 좋을까? 그리고 보다 근본적인 문제가 있다. 우리는 지금 '반복하는 단어가 없는 최대문자열' 을 달리 나타내보고 있는데, 그렇다면, '도로 체계' 라고 본 해석에 따르면 그 최대문자열은 무엇을 뜻할까? 최대문자열을 통해서 우리는 어떤 교훈을 얻을 수 있을까? (멈추고 생각해보라, 그리고 자기만의 해석을 했다면 어떤 교훈을 얻을 수 있을까? 생각해보라. )
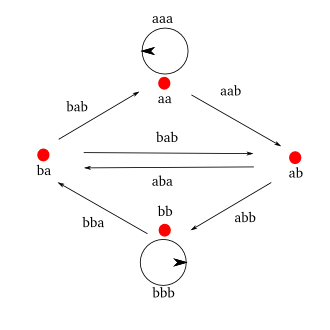
아래 그림을 보자. 이 경우의 최대문자열을 도로체계로 왼쪽 그림에 나타냈다. 오른쪽 그림은 그것을 '한번씩' 거쳐가는 한 예다. 이것은 무엇을 말하고 있을까?
그렇다. 이 그림들이 도시 도로 체계라고 했을 때, 4개 도시를 연결하는 8개 길을 '딱 한번씩만' 거쳐가는 방법을 말해주고 있다. 도시마다 들어오고 나가는 길이 둘씩이라는 사실에 주의하라. 이런 조건을 만족하는 도로 체계가 있고, 그 안에 도로 표지판을 만들거나, 도로 공사를 하거나, 도로가 안전한지 점검하는 사람이 있다고 하자. 반복해서 길을 왔다갔다 하지 않고 모두 들리되, 한번 씩만 들리고 싶은 경우, 그는 출발하기 전에 이와 같은 '최대문자열' 문제를 풀어봄으로써 자원을 엄청나게 절약할 수 있다. 여기서 핵심 문제는 다음과 같다.
- 어떤 길에서든 다른 길을 항상 갈 수 있는가?
- 모든 길을 다 갈 수 있는가?
우리의 예에서는 어떤 길에서든 다른 길로 갈 수 있고, 모든 길을 갈 수 있었다. 그렇다면 우리가 함께 본 예를 특수한 경우일까? 다음 문제를 스스로 생각해보라.
|
'최대문자열'을 도로체계로 표시한 경우 위의 두 문제에 대해 항상 '그렇다'고 보장할 수 있을까? |
답을 못었다면 아래 더 복잡한 경우, 단어 길이가 4 인 경우를 보면서 터득하면 된다.
4 글자 단어의 경우
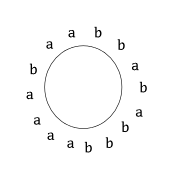
이제, 앞에서 했던 일반화(1)를 다시 참조하면서, 단어가 4글자로 이루어진 경우를 보자. 이미 고찰했듯이, 단어가 4글자라고 가정하면, 4글자 단어는 16개가 가능하고 따라서 최대문자열의 길이는 19개다. 그렇다면 앞에서 한 해석대로, 이것을 '고리'와 '길'로 나타내보기로 한다.
|
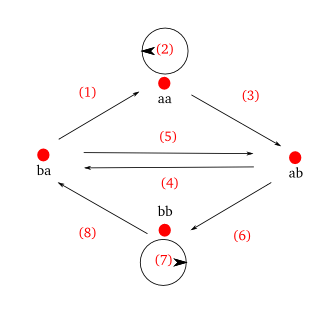
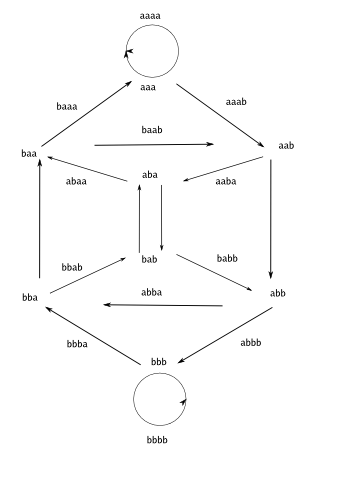
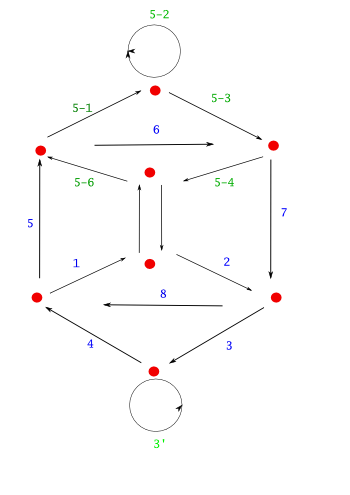
아래 그림 왼쪽은 단어길이가 4인 경우, 가능한 단어들을 '도로'로, 그리고 '연결하는' 부분을 도시로 표시해놓은 것이다. 그리고 오른쪽은 이것들을 모두 가되 한번씩만 가기 위한 첫번째 시도를 해본 것이다. 숫자는 순서를 나타낸다. 이때 bba 에서 꼭 출발해야 하는 것은 물론 아니다. 어디서든 출발할 수 있다.
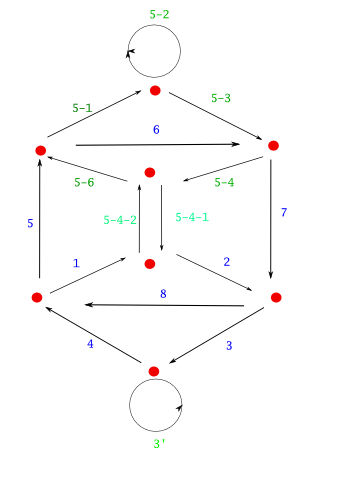
위의 오른쪽 그림을 보면 한번 씩은 들리되, 모든 도로를 다 거치지 않았다는 사실을 알 수 있다. 모든 도로를 거치기 위해 완전히 다른 방법을 쓸 필요 없다. 이미 시도해 본 것을 보완해가면 한번 씩 들리면서도 모두 다 갈 수 있다. 아래 그림을 보라. 왼쪽 그림은 앞에서 시도한 것 중 5 도로에서 6 도로로 가는 사이에, 들리지 않은 길을 보완했다. 오른쪽 그림은 이제 모든 도로를 다 들렸다.
위의 그림들은 한번씩만 모두 다 들렸다는 것에 주의하라. 따라서 우리가 도로 점검원이라면 모든 도로를 다 보고, 한번씩만 거치는 경우는 모두 열여섯개 경우가 가능하다. 이제 마지막으로 다음 질문에 답해보라.
|
이제 단어의 길이가 5, 6, 7 로 늘어갈 경우에도 항상 '한번씩' '모두' 들릴 수 있을까? 물론, 그럴 수 있다. 다만, 있다는 것은 확실하지만, 구체적으로 어떤 것인지 찾는 것은 복잡해진다. 따라서 우리가 한 방법보다 더 효율적으로 최대문자열을 찾는 방법을 생각하지 않을 수 없다. 어떻게 하면 될까?
현대 과학 기술에 응용
단어가 없는 최대문자열은 현대 과학에서 매우 유용하게 쓰인다. 간단히 나열만 해보겠다.
- 지구에서 달, 금성의 거리를 재기 : 알파벳이 둘인 경우를 본다. 하나는 펄스가 있는 것을 표시하고 하나는 없는 것을 뜻한다. 반복하는 단어가 없도록 최대문자열을 만든다. 단어길이가 50인 경우를 생각해보면, 단어 반복이 없는 최대문자열은, 의 길이로 나타낼 수 있다. 그 수를 풀어보면 수십억 쯤 된다. 이것을 발사한다. 달이나 금성을 맞고 반사되어 돌아오는 열을 봐서 반복되는 부분을 찾는다. 수십억 글자가 지나고 나서야 반복하는 50글자 단어가 나올 것이다. 반사되어 돌아온 시간을 계산한다.
- 오류발생 자기 점검 프로그램 : 컴퓨터 안에는 안에서 오류를 일으킬 것을 대비해 스스로 점검하는 프로그램, Built-in self test (BIST) 가 있다고 한다. 여기에 shift register sequence 가 중요한 역할을 하고 여기에 위의 문제가 쓰인다고 한다. 전자 기기에 매우 중요한 역할을 한다. 에 두루 쓰인다고 한다. shift register sequence는 CDMA 방식 이동전화에서 개인 신호를 확인하는 데도 쓰인다고 한다.
- 암호 : 원래 정보를 두 문자로 코딩한다. 충분히 길게 해서 단어 반복없는 최대문자열을 중간에 섞는다. 여기엔 반복이 없도록 했기 때문에 매우 무작위적으로 나타나 해독하기가 어렵다. 이것을 날려 보낸다. 그렇다면 중간에 다른 데서 이 신호를 잡았다고 해도 해독하기가 어려울 것이다. 받는 사람은 섞인 최대문자열이 무엇인지 알고 있어서 그것이 어디에 있는지 찾아내 빼내고 해독하면 된다.
- 인도의 고대 시와의 연관성 : 강세와 음절이 중요한 역할을 한 시의 체계에서, 약세와 강세 부분을 a , b 로 표시한다고 해보자. 시는 세음절로 짓되 8개 운율 모두 나와야 한다고 하자. 그렇다면 이것을 구현하는 방법은 앞에서 우리가 보았던 단어길이 셋인 최대문자열의 경우와 비슷하다. 실제로
이라는 3 음절 8개 운율 모두가 나온 경우로, 우리의 abbbabaaab 라 바꾸어 표시할 수 있다.
일반화 2
지금까지 문자열이 직선 모양으로 쓰는 경우를 보았고 그것이 어떻게 응용되는지 살펴보았다. 알파벳으로 할 만한 글자는 둘 뿐이고, 단어 길이도 2인 경우부터 시작했다. 그리고 단어 길이를 3, 4 로 더 넉넉하게 늘려가면서 일반화했다. 이를 더 일반화해볼 수는 없을까? 물론 더 확장할 수 있을 것이다. 그럴수록 문제를 풀기가 더 어려워질 것이라는 것을 짐작할 수 있다. 예를들어, 자세히 고찰하지 않겠지만, 다음의 문제를 생각해볼 수 있다.
알파벳이 a , b , c 로 셋이 있는 경우
알파벳이 셋이고 단어의 길이가 10 이라고 가정해보자. 이것을 도로 체계로 표시한다고 해보자. 도시 마다 드나드는 길이 셋씩일 것이다. 최대문자열을 표시하는데 등장하는 단어(길)는 몇 개일까? 앞에서 알파벳이 둘인 경우, 바퀴열의 길이는 이었다는 사실을, 그리고 그로부터 도로의 수도 그와 같다는 사실을 알고 있다. 마찬가지로 알파벳이 셋이고 단어의 길이가 10인 경우는 무려 의 바퀴열, 따라서 도로의 수도 그만큼이 된다. 이것은 60,000 개 정도의 도로가 있다는 말이 된다. 도시의 수는 개 일 것이다. 다음 질문에 답해보라.
|
알파벳이 셋이고, 단어의 길이가 열 개인 경우를 도로체계로 표시한다고 하자. 어떤 하나의 도시에서 최대 몇 번을 거치면 다른 도시로 도달할 수 있을까?[5] |
그런데, 이렇듯, 한 도시에서 드나드는 길이 셋인 경우 이 도로체계를 모두 연결하되 딱 한번씩만 들릴 수 있도록 하려면 어떻게 하면 될까? 물론 그런게 있다는 것은 분명하다. 하지만, 이제 이것은 매우 복잡하다. 따라서 어떻게 하면 더 빨리 찾을 수 있을까가 문제가 될 것이다. 아직까지 쉽고 간명하게 찾을 수 있는 방법은 찾지 못했다고 한다. 여러분이 한번 시도해봄이 어떨지?
직선으로 나타내지 않고 직사각형으로 표시하는 경우
이제 다른 일반화의 경우도 보자. 문제는 이렇다. 이제 문자열을 직선으로 표시하는 것이 아니라, 어떤 방법으로 직사각형 모양의 틀에 문자열을 표시한다면 어떻게 될까? 예를들어, 알파벳이 둘이라고 가정하고 그림과 같이 직사각형 모양이라고 보자.
- aababaaaba
- babbaabbab
- abbaababab
상자안에 있는 위아래로 두개씩 2X2 정사각형이 단어를 이룬다고 하자. 이렇게 했을 때, 어떤 단어도 겹치지 않도록 하는 최대 직사각형의 설계는? 이 문제는 실제로 로봇 공학에 적용할 수 있다. 2X2의 발판을 가진 로봇이 직사각형 모양의 길을 상하좌우로만 옮겨 다닐 때, 위치를 파악한다고 하자. 단어반복이 있다면, 어떤 위치에 있는지 헷갈리는 경우가 나올 수 밖에 없다. 직사각형 판을 '단어 반복없는 최대문자열'로 만들어놓아야만 로봇이 이동하면서 발판 아래의 정보를 사람에게 계속 전달해줄 때, 우리는 그 로봇이 현재 어떤 위치에 있는지 정확히 알 수 있다.
Note
- ↑ (American Standard Code for Information Interchange ;ASCII. 아스키, 또는 애스키라고 부른다. 영어 단어와 기초적인 문자기호를 넣고 나타낼 때의 기본 코딩 체계다.
- ↑ 16개의 기호를 쓰는 16진 체계(hexadecimal system) 으로도 바꿀 수 있다. 그러면 love 는 6c 6f 76 65 이고 mathematics 는 6d 61 74 68 65 6d 61 74 69 63 73 다.
- ↑ 중간에 반복하는 단어가 나와 더 진행 안해도 되겠지만, 틈틈히 반복을 확인하지 않고 그림만 그려볼 경우 가지의 끝에는 , 다시 말해 1024 개의 열매가 열려 있을 것이다. 1024의 열매들이 열린 가지들에 세개씩 짝을 지어 가지에 표시를 하고 뿌리로 다가가면서 반복 부분을 검토하는 것이 빠를까? 아니면, 가지를 새로 뻗칠 때마다 반복을 확인하면서 가는 것이 더 빠를까?
- ↑ 8개다. (왜 그럴까?)
- ↑ 놀랍게도 9이면 충분하다. 알바펫이 둘이었던 경우를 생각해보면 간단하다. 1234567890 에서 abcdefghij 로 간다고 생각해보라. 이때 1 부터 0까지, a 부터 j는 모두 알파벳중 어느 하나라고 가정한다. '연결한 지점'들로 1234567890 에서 234567890a로, 다음은 34567890ab로 해가면 결국 9 단계를 거쳐 abcdefghij 로 갈 수 있다. 도로의 수가 6만 개 정도 되는데도, 어떤 도로에서 다른 도로로 9개만 거치면 갈 수 있다 !
 문자열을 가지고 놀기 로 돌아가기
문자열을 가지고 놀기 로 돌아가기