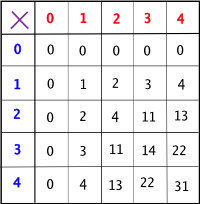Math Mail 05: 두 판 사이의 차이
편집 요약 없음 |
(차이 없음)
|
2008년 4월 7일 (월) 14:18 기준 최신판
봄이, 퍼지고 있다. 보이니, 명훈아? 들리니? 새싹이며 꽃망울 터져나는 소리?
봄이 성큼 걸음을 내딪는 날 신선한 바람을 쐬러 나갔단다. 자전거 산책을 했어. 그러다 흥미를 끄는 게 있으면 멈춰 사진도 몇 장 찍었어. 사진은 나중에 보여 줄께. 약속하마. 해질녘까지 있을까 하다가 서둘러 들어왔단다. 오늘까지 쓰고 싶어서 시작했던 수학 편지를 마저 끝내는 게 좋을 것 같았어. 마침 곱셈이 나올 때라, 자꾸 이런 생각이 드는 거야 : '곱셈 이야기를 어떻게 풀어 쓰면 좋을까?' 하고 말야. 생각만 하고 있으면 같은 게 빙빙 돌고 있어서 써버리는 것이 나을 것 같았단다. 그래야 앞으로 한 발 더 나아가 다른 이야기도 생각할 수 있을 것 같았어. 어제 저녁 산책을 할 때, '와, 좋은데 !'라는 느낌이 가슴을 팡 때린 좋은 생각이 났는데, 글쎄, 그것을 바로 적어두지 않고 다른 생각을 하다 들어왔더니 잊어버렸지 뭐니? 어제 밤과 오늘 아무리 생각해봐도, 다시 그 생각은 떠 오르지 않는구나. 도대체, 그때 삼촌에게 들었던 그 생각은 '어디서 왔다가 어디로' 간 것일까?
오늘은 곱셈 이야기를 해볼까 해. 지난 편지에 덧셈을 어떻게 하는지와 그 성질을 보았지? 덧셈을 잘 이해했다면 오늘 삼촌이 하는 이야기는 그리 어렵지 않게 받아 들여질 거야. 할 이야기의 핵심만 미리 이야기를 해볼까?
- 곱셈이란 무언가?
- 곱셈은 어떻게 할까?
- 곱셈도 덧셈처럼 그런 '좋은' 성질이 있을까?
이런 이야기들인데 덧셈에서 했던 질문들이랑 비슷하지? 어떤 것도 '이것이 정답이다.' 고 말하지는 않을거야. 그렇게 딱부러지게 말하기 어렵거든. 대신 삼촌의 생각을 말해 볼께. 명훈이가 읽다가 석연치 않은 게 있거든 함께 더 생각해 보자꾸나.
지난 편지에서 덧셈은 교환과 결합 법칙이 성립한다고 했지? 그걸 기호로 간단히 쓰면, a, b, c 가 자연수라고 했을 때, 교환은,
이고, 결합은,
라고 했어. 앞은 셈하는 수를 바꾸어 써도 된다는 것이고, 뒤는 셈의 순서를 바꾸어도 해도 결과는 다르지 않다는 것이었어. 두 성질이 왜 그렇게 될 수 밖에 없나 ? 라는 질문에 대해서, 콕 집어서 바로 이거다! 라고 말은 못하지만, 그것을 믿어 줄만한 이유에 대해서는 생각해 봤어. 덧셈을 할 때는 두 수를 셈하는 것이니까 무엇부터 셈을 할지 괄호를 쳐주는 것이 옳아. 하지만 덧셈의 그런 성질들 덕분에 우리는 괄호 치기에 얽매지 않아도 되었어.
는 그냥 명훈이가 마음에 드는 순서대로 하면 돼. 마찬가지로,
의 셈도 그래. 게다가 이것은 같은 수들 끼리니까 정말 쉽지. 삼촌은 이렇게 해볼께.
그런데 명훈이는 이렇게 했다고 해보자.
계산의 결과는 어떻게 되지? 그렇지 물론. 그런데 어떻게 그렇게 되는 걸까? 원칙대로, 그러니까, '명훈이 방식'으로 하면
로 되겠지. '삼촌 방식'으로 해도 결과는 같을 거야. 어떤 순서로 하든 상관없으니까. 게다가 수가 모두 2 로 같기까지 해.

어떤 식으로 하든, 결국 '2를 다섯 번 더했다' 는 말이 돼. 오른쪽에 그림으로 예를 들어봤어. '빨간 공 모델'로 나타내 본 거지. 이런 식으로 '같은 수가 여러 번 나오는 덧셈'을 간단히 나타낼 수는 있는 셈이 있겠지? 이것을 보통 곱셈이라고들 해. 기호로는, 간단히
로 쓰지. '더하기' 기호를 45도 정도 기울여 '곱하기'를 나타냈어. 앞의 표현을 '2를 5 번 곱했다' 고 받아들이면, 그때는 덧셈으로 곱셈을 '정의'해 준 것이 돼. 다시 써볼께.
앞으로도 종종 나올거야. 기호 " := " 은 " 왼쪽에 있는 것을 정의(definition)해주면 오른쪽에 풀어 쓴 뜻이다. " 라는 말을 줄여서 쓴 거라고 이해해다오. 간단히 쓰기 위해서 기호를 쓴거야. 다른 사람들은 다르게 쓰기도 해. 라는 기호를 쓰는 사람도 있고, 라는 기호를 쓰기도 하고, 더 있어. 그건 말하는 사람마다 편리하도록 하는 거니까 미리 정해주기만 하면 돼. 덧셈도 그렇고 곱셈도 기호로 쓰잖아. 자연수도 기호로 쓰고. 그런데, 덧셈 기호는 대부분 + 로 쓰는 반면, 곱셈 기호는 를 쓰기도 하고, 그냥 가운데 점 ' ' 을 쓰기도 하고, 간단히 ' * ' 를 쓰기도 해. 세째 편지였던가? 자연수도 오랫동안 저마다 다른 기호들이 경쟁하잖아. 그러다가 서서히 하나로 통일 되어 가듯이 셈을 나타내는 이런 기호들도 그렇고 수학에서 다른 기호들도 그래. 우리는 지금도 진화하고 있어.
어쨌든, 곱셈을 그런 식으로 '덧셈을 통해서' 정의해주는 방식으로 해 보았는데, 수 천 년 동안 사람들은 자연스럽게 그렇게 이해했어. 명훈이도 아마 초등학교 때 그렇게 배웠을거야. 그런데 꼭 그럴까? 그렇다고 쉽게 뱉아버리기엔 조심스러운 구석이 있어. 그렇게 이해하면
을 이해하는게 까다로와지거든. 이건 쉽지. 그런 '정의'를 받아들인다 해도,
- 이나 이나
모두 0 이야. 왜냐하면 그 정의대로 하면 그것들은,
이니까. 그것은 0 의 덧셈과 덧셈이 가진 성질을 이해했다면 뻔한 거잖아.
하지만, 은? 앞의 '정의'대로 하면, '2를 한 번도 안 더했다'는 말로 해석해야지? 3보다 크다고 말하긴 어려울 것 같아. 왜냐하면 3 안에는 2가 한 번 들어있다고 볼 수 있으니까. 그렇다면 그것이 0 이어야 할까? 1 일 수도 있지 않을까? 0도 아니고 1도 아니면서 2가 한 번도 들어있지 않은 다른 어떤 수일 수는 없을까? 명훈인 어떻게 이에 대해 답을 하겠니?
|
도 0 이고, 도 0 이고, 도, 모두 0 이어야 할까? 왜 그럴까? |
생각해봤니? 생각만 해본 게 아니라, 공책에 나름대로 명훈이 생각을 써보았어? 무엇을 적었을까 몹시 궁금하구나.
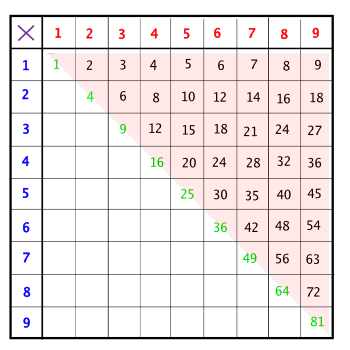
곱셈은 어떻게 할까? 덧셈과 비슷해. 우리는 10진법을 기본으로 쓰고 있기 때문에 우선 기본으로 이것을 보자꾸나. 곱셈도 표 하나만 알고 있으면 충분해.
반만 써보았어. 나머지 반은 스스로 공책에 채우면 될거야. 사실은 채우지 않아도 되겠지. 다음에 보겠지만, 곱셈도 덧셈처럼 '교환'해도 되거든. 이 표만 알아도 그 '교환'의 성질을 이해하고, 여기에 간단한 알고리듬만 적용하면 곱셈할 수 있어. 스스로 풀어보면서 어떻게 하는지 '알고리듬'을 공책에 써 보겠니?
|
의 곱셈을 하면서, 어떤 방법으로 하는지 단계 단계를 공책에 적어 보아라. |
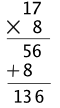

이런 식의 계산은 초등학교 때 부터 지금까지 수 천 번은 했을테지? 지금은 쉽지? 하지만 기억을 더듬어 봐. 처음 이것을 배웠을 때, 우선 '구구단' 이라고 부르는 곱셈표를 먼저 외어야 했어. 노래하듯이 운율을 넣어서 했을 거야. "이~ 일은 이, 이~ 이는 사, 이 삼은 육, .... , 구~ 구! 팔십 일" 이렇게 말야. 그리고 그 다음엔 큰 수에 대해 곱셈하는 알고리듬을 배워 왔단다. 아마 여러 번 실수하면서 배웠을 걸. 그렇게 하다 보니 지금은 쉬워 진거야. 삼촌도 한 번 적어 볼께. 옆의 그림에 두 방법으로 표시해 봤어. 둘다 '줄맞춰 세로로 쓰기' 하는 방법으로 해 본 거야.
- 옆의 그림의 위의 방법 (네모 칸 안의 방법)
- 7 곱하기 8 을 한다. 이를 위해 곱셈표를 본다. 56이다.
- 1 곱하기 8에 해당하는 곱셈표를 본다. 8 이다.
- 자리수를 맞추어 더한다. 결과는 136
- 옆의 그림 아래의 방법
- 7 곱하기 8 을 한다. 이를 위해 곱셈표를 본다. 56이다.
- 10의 자리인 5를 '올려두고' (잠시 기억해 두고) 1 곱하기 8에 해당하는 곱셈표를 본다. 8 이다.
- 자리가 같은 것 5와 8 을 더해서 13을 얻는다. 이것은 130이다. 이것과 처음 얻은 6 을 더한다. 결과는 136.
결국 모두 1단계에서 56 을 하고, 2 단계에서 80을 곱셈표를 참고해서 얻은 다음 '자릿수법'을 써서 어울리는 자리에 있는 수들끼리 더해서 얻은 것이지. 같은 알고리듬이지만 조금 복잡한 예를 볼까?
|
조금 복잡해서 귀찮을지 모르겠지만, 한 번은 꼭 스스로 써보기 바란다. 그렇게 하고 나면 이제 곱셈이란 무엇인지 알 만할거야. 그런데 과연 그럴까? 우선 10진법 곱셈을 더 확인해 보고 다른 경우도 보기로 하자. 공책에 풀어 봐라.
|
바로 앞의 문제 1abcde 란, 예를 들어 13457 처럼 써 있는데, 3, 4, 5, 6 이 살짝 가려져 있다는 뜻이야. 물론 이게 답은 아니야. 스스로 해 봐~
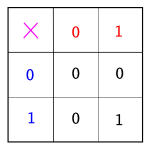
자, 그럼 이제 10진법의 곱셈이 아니라 다른 경우의 '곱셈' 에 대해서도 보자. 이것을 제대로 쓸 수 있다면 곱셈을 하는 방법은 더 많이 알게 된 셈이지. 먼저 삼촌이 옆에 2 진법일 때 곱셈표를 만들어 보았어. 정말 간단하지? 삼촌은 별로 마음에 안들지만, 십진법의 곱셈표를 '구구단'이라고 부르니까, 이 표는 '일일단' 정도 되나? 2진법의 곱셈표는 참 쉽지? 곱셈표를 외우지 않아도 될 정도야. 내친김에 5진법의 곱셈표도 보자.
이건 그럼 '사사단' 이라 불러야겠구나. 아무튼, 삼촌은 그냥 '4진법의 곱셈표' 라고 부르는게 더 낫다고 생각해. 구구단도 십진법의 곱셈표라고 부르는 게 나아. 이름이야 어떻든, 이 표를 외우고 있지 않다고 생각해보겠니? 또, 10진법의 곱셈표를 외우고 있지 않으면 어떻게 할까? 아주 오래 전 사람들은 그것을 일일이 덧셈을 여러번 해야 했을 거야. 마치 처음에 우리가 2을 다섯번 더한 것 처럼. 그렇게 되면 곱셈은 상당히 어려운 셈이 되는 거지. 고대 로마나 이집트 사람들 숫자 썼던 기억나니? 그 사람들은 아까 17 곱하기 38 같은 경우 어떻게 했겠니?
곱셈표를 외우고 자릿수법을 이용해 '적당한' 알고리듬을 쓰면 곱셈은 그리 어렵지 않지? 이제 그럼 공책을 펴고...
|
앞의 네 문제를 잘 풀어내면, 곱셈 하는 법은 이제 깨달았다고 볼 수 있어. 명훈아, 혹시나 해서 하는 말인데, 이미 이런 진법을 10진법으로 바꾸어서 10진법의 곱셈을 한 다음, 그것을 다시 진법을 바꾸어 답을 쓰지는 말아다오. 곱셈을 어떻게 하는지 분명하게 인식하기 위해서 해보는 것이니까, 꼭 '알고리듬 대로 직접' 해 봐. 알았지?
아휴, 오늘 편지는 곱셈을 다 못끝내고 다음으로 넘겨야겠네. 아쉽다. 그렇지만, 어쩔수 없어. 앞에 있는 것만 제대로 풀어 보는 데도 명훈이가 너무 고생을 하지나 않을까 삼촌이 은근히 미안해지기 시작했거든. 오늘은 이만하고 다음 편지에 이어서 하자. 다음 편지에
- 곱셈은 어떻게 할까? 에 대해 조금만 더 이야기하고,
- 곱셈도 덧셈처럼 그런 '좋은' 성질이 있을까?
로 이야기를 풀어가자꾸나. 자, 그럼 오늘은 여기까지. ![]()
처음에 썼지 ? 봄이 번지는 모양, 봄이 터져 나는 소리? 그런 걸 듣고 보기에 지금 우리가 사는 곳은 각지고 단단하고 시끌벅적하긴 해. 그렇지만, 가끔, 선자리에서 빙 둘러도 보고, 위로도 아래로도 보기 바란다. 그러다 어디 마음이 닿거든 거기 마음을 조금 나눠 주렴.

 수학 편지 대문으로.
수학 편지 대문으로.