Math Mail 10

명훈 안녕 !

삼 주째, 또 비가 오고 안개가 꼈다. 놀랍다. 이렇게 되면 과연 다음 주 수요일도 비가 오고 안개가 낄까? 궁금해지지 않니? 일 년 내내 이렇게 되기는 힘들테니 언젠가는 어떤 수요일에 비도 안오고 안개도 끼지 않은 날이 있겠지만, 삼촌은 다음 주 수요일이 벌써 부터 기대가 되는구나. 사실, 어떤 일이든 어느 정도 규칙이 나타나면 그 다음은 어떻게 될까? 호기심이 생기기 마련이거든. 이런 호기심이 사람이라는 생물의 별난 특징일거야. 눈에 잘 안보이지만 어떤 규칙을 찾고 그것으로부터 감추어진 세상의 진실을 보려고 마음의 눈을 기르지. 그리고 그게 잘 보이면, 이제 그것을 응용해 가면서 새로운 것을 발명하고 창조해서 문명을 발전시켜. 그런 것을 가장 잘 드러내는 것이 아마 수학 공부일지 몰라.

명훈이에게 그동안 아홉 개의 수학 편지를 보내고 나서 삼촌은 고민이 생겼어. 스스로 질문을 던졌거든. 다름 아니라, "자, 이제 길을 어디로 잡아 나가는게 좋을까? " 라는 물음이야. 우리는 지금 '수'를 보면서 자연수와 덧셈 곱셈을 보았고, 그 다음으로 지수셈, 뺄셈과 나눗셈을 살짝 보았어. 이제 길은 분수 또는 유리수로 갈 것인가, 아니면 음수를 캐볼까 고민할 수 밖에 없거든. 명훈이야 학교 교과서에 따라 공부하니까 그 순서를 따라 주면 되지만, 사실 교과서를 만드는 분들도 고민할 걸. 그 분들도 어떤 순서로 하는게 옳을까 고민하고 모여서 토론하면서 만들었을거야.

어떤 길로 가든 조금만 더 가면 길은 만나게 될 테지만, 삼촌이 설명을 하려니 난처하더라. 고민이 되었어. 게다가 며칠 강원도 산골에 다녀왔단다. 약속도 있었고. 그래서 편지가 며칠 늦어졌구나. 생각에 생각을 거듭하다 삼촌은 오늘 음수 쪽으로 방향을 잡아보았다. 음수. 이건 참 묘한 것이야. 이미 배웠다면 알겠지. 음수가 무엇인지. 하지만, 이것은 참 이상한 수란다. 그래서 설명이 그리 만만하지는 않아. 하지만, 지난 편지에서 뺄셈을 조금 자세히 들여다 보았던 것을 이어서 마저 더 이야기를 해 볼께. 잘 들어보고 혹시 궁금한 게 생기면 함께 더 이야기를 나눠보도록 하자꾸나.

지난 편지에서 뺄셈을 했는데, 덧셈이나 곱셈과 다르게 뺄셈은 조건이 붙어. 우리에게는 지금 자연수와 0 만 있다는 사실을 환기해보렴. 어떤 조건이냐면, 작은 수에서 큰 수를 뺄 수 없다는 거야.

$3-2$

는 어렵지 않지 않아? 단순하게 생각하면 셋에서 둘을 덜어내는 거니까, 1 이 되겠지. 또는 이미 말한 것 처럼, 3-2 란 셈은

2에 얼마를 더하면 3 이 나오는지 그 수를 찾는 절차

라고 했으니 그렇게 봐도 1이 되겠지. 그렇다면, 이것은 어떻게 될까?

$2-3=?$

이것을 우리가 이해한 대로 하면

3에 얼마를 더하면 2 가 되는지 그 수를 찾는 절차

겠지. 그런 수는 없어. 그렇지 않니? 덧셈은 항상 '보태어가고 수를 키워가는' 그런 성질을 가지고 있잖아. 그게 덧셈이라는 셈의 고유한 특성이거든. 그렇게 보면, 큰 수에서 더해서 작은 수를 나오게 하는 수는 없는게 당연하지. 이 말을 정리해서 보면, 뺄셈이란 이런 조건이 함께 따라 다녀야 한다는 것을 뜻해.

$b>a$ 이면 뺄셈 $b-a=?$

라는 식으로, 큰 수에서 작은 수를 빼라는 조건이 붙어.

아, 참, 우리는 아직$b>a$ 라는 말을 정확히 하지 않았구나. 이것에 대해서도 이미 알고 있지? 하지만, 다시 생각해보면, 과연

b 가 a 보다 크다.

라는 것은 정확히 무슨 뜻일까? 어떤 수가 주어지면 간단한 하겠지? 예를 몇 개 들어볼께.

• 사과 셋과 사과 둘이 있으면 사과 셋 > 사과 둘.
• 빨간 공 아흔 아홉 개 와 빨간 공 여든 여덟 개 있으면 빨간 공 아흔 아홉 > 빨간 공 여든 여덟 개.
• $100^{3}>10^{2}$

이런 식이겠지?

사과 다섯에서 수박 셋을 빼면 어떻게 될까?

다시 말해 기호

$b>a$

는 b 와 a 가 있을 때, 그것들을 '비교' 하는 것이지. 지금까지 어떤 자연수나 또는 0 중 아무거나 a와 b 둘을 꺼냈을 때, 그것들을 엮는 기호들이 무엇이 나왔는지 돌아 볼까?

$a+b,\ a\times b,\ a-b,\ a\div b,\ a^{b}$

같은 것들이 있었어. 이것들만 있었을까? 아냐. 하나 더 있단다. 너무 자주 나와서 놓치기 쉽지만,

$a\ =\ b$

도 있었어. 위에 있는 다섯 가지는 자연수나 0 중에서 어떤 두 수가 나오면 그것을 셈해서 새로운 수로 대응시키는 거야. 그에 비해, '같음'을 나타내는 ' = ' 는 새로운 것을 나타낸다기 보다는 비교만 하는 게 조금 다르지. 마찬가지로$b>a$ 도 그래. 비교해서 둘 사이의 관계가 어떤지를 말할 분이야. 그렇다면 어떤 관계일까? '크다' 또는 '순서가 뒤다' 라는 것을 '수학적으로' 달리 정확히 말하면 어떻게 할 수 있을까? 간단해.

$b>a$ 는 a 에 어떤 자연수를 더해서 b 가 될 수 있다는 것을 말한다.

됐지? 이 말을 기호를 써서 달리 말하면,

$b+x=a$ 가 되는 x 가 있으면 $b>a$.

이렇게 말할 수 있지? 뭐 똑같은 말을 이렇게 복잡하나 싶겠지만, 다 이유가 있어. 자연수 와 덧셈, 같음 이라는 말을 표현해서 더 정확해졌어. 이럴 때 만약 x 가 0 도 될 수 있으면 어떻게 할까? 그럴 땐 새로운 기호를 쓰기도 하는데, 혹시 이런 기호 본 적 있는지 모르겠구나.

$b\geq a$

앞으로는 이 기호를 쓸 때는 b 가 a 보다 크거나 또는 같다 라는 뜻이야. 2, 7 , 88, 99 처럼 어떤 수가 분명하게 드러나면 이렇게 복잡하게 말하지 않아도 되지 물론. 하지만, 수이긴 수인데 그것이 아직 무엇일지 모르는 $a,b,c$ 같은 것으로 모호하게 나타나면 항상 조심하면서 정확히 말을 만들어줘야해. 안그러면 자칫 엉뚱한 결과가 나오기도 하거든. 더 분명하고 정확하게 해서 실수를 줄이는 것, 이것이 바로 수학의 특징이지. 그래서 대충 넘어가려는 사람들에게 수학은 끔직한 과목이 돼.

말이 조금 샜구나. 다시 돌아가자. 뺄셈으로 돌아가 말을 이어서 해 볼께. 자연수와 0 들 사이의 뺄셈에는 항상 어떤 조건이 붙는다고 했지? :

$b\geq a$ 이면,$b-a$ 얼마인가 ?

라고 해. 잘 들여다보면 이 문장의 '조건'과 '결론' 부분은 상당히 연관성이 있어. 어떤 것이냐면, 조건 부분을 보자.

$b\geq a$ 는 a 에서 더해서 b 가 되는 자연수 또는 0 이 무엇인지는 모르지만 아무튼 있다.

는 것을 뜻하고, 결론 부분

$b-a$ 는, a 에 더해서 b 가 되는 자연수 또는 0 을 찾아내라.

고 말하고 있는 거야. 그래서,

$0-4$

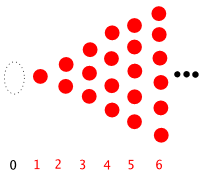
같은 문제는 풀 수가 없게 돼. 마치 옆의 그림처럼, 자연수를 빨간 점들로 묘사해보면 왼쪽으로 올수록 수가 점점 줄어들다가 마침내 더는 갈 수 없게 되버려.

나눗셈을 말할 것 같으면, 문제는 더 복잡해진단다. 오늘은 우선 뺄셈에 우리 관심을 집중할 것이기 때문에 나눗셈에 대해서는 다음에 이야기할께. 그런데, 한 번 생각해 봐. 덧셈과 곱셈은 그렇지 않았는데, 하필 뺄셈과 나눗셈이 들어서면 무언가 꼬이고 얽혀드는 것 같지 않니? 이런 제약을 벋어날 수는 없을까? 자연수와 0 만 있는 지금의 상태로는 어쩔 수 없었어. 하지만, 방법이 아주 없는 것은 아냐. 뺄셈을 할 때 그런 제약이 있었던 것은 우리가 수의 세계를 자연수와 0 으로 제한하고 있기 때문이지. 저, 위의 그림과 다르게 묘사해볼께. 아래 그림을 보자. 여기서는 수가 크다고 해서 더 크게 표시하지 않고, 자연수마다 평등하게 본 거야. 순서만 중요하게 볼 뿐이지. 그래서 수가 커도 빨간 점 하나로 찍었어.

자연수와 0 을 반드시 바로 위의 그림처럼 떠올려야만 것은 아냐. 그렇다고 그렇게 묘사해 볼 수 없다는 것도 잘못이지. 어쨌든, 빨간색 점들은 자연수와 하나씩 대응시켜서 해 두었어. 오른쪽으로는 끝없이 가는데, 왼쪽으로 오면, 0 에서 막힌 구조야. 여전히 답답해.

수로 돌아와보면,

$0,\ 1,\ 2,\ 3,\ \dots ,\ 99,\ 10^{2},\ 10^{2}+1,\ \dots ,\ 999,\ 10^{3},\ 10^{3}+1,\ \dots ,\ 10^{10}-1,\ 10^{10},\ 10^{10}+1,\ \dots ,\ 10^{10^{10}}-1,\ 10^{10^{10}},\ 10^{10^{10}}+1,\ \dots$

이렇듯 오른쪽으로는 '하나 씩' 증가해가면서 끝없이(!) 계속 되는데, 자연수는 왼쪽으로는 막혀있잖아. 이렇게 막힌 게 문제였어. 어떤 기준을 정하고 왼쪽과 오른쪽, 위와 아래, 많고 적음, 높고 낮음과 같이 대칭하고 있는 경우는 우리가 살아가면서도 흔히 만나지 않니? 한 두 개만 예를 볼까?

• 물이 어는 점을 기준으로 그것을 0 도로 하고, 섭씨 영상과 영하,
• 가진 재산이 하나도 없고 부채도 없는 상태를 0 으로 하고, 쓸 만큼 가진 것과 빚으로,
• 우리나라에서는 인천만 평균해수면의 높이를 0 으로 하고 육지는 해발 고도로 하잖아. 해저는 그것에 대칭적인 깊이겠지?

이제 명훈이가 스스로 찾아보겠니? 마음의 눈을 열고 선자리에서 사방 팔방을 잘 둘러보면 꽤 보일거야.

우리가 살아가면서 만날 수 있는 사례들을 스스로 찾아서 채워 보겠니? 바로 앞에서 봤던 것과 비슷한 개념의 예들 말야. 최소한 다섯개 정도?

그렇듯, 0 을 기준으로 자연수에 대칭적인 수들이 없을까? 없다면 그게 더 이상하겠지. 세상에 자연수만 있을까? 삼촌이 보기엔 '자연스러운 수만 있다' 는 생각이 참 부자연스러워. 0 만 해도 그랬어. 0 이 수로 온전히 받아들여지는 데 수 천 년이 걸렸다고 했잖아. 그런데도 이제와서는 자연스럽게 되었지. 마찬가지로 0 의 '반대편'에도 틀림없이 수가 있어. 그런데 있다면, 과연 어디에 있을까? 이 문제를 한번 생각해보겠니?

0 을 기준으로 자연수에 대칭하는 수가 있다면 그 수들은 도대체 어디에 있는 것일까?

생각만 하지 말고 그 생각을 꼭 써 보기 바란다. 깊이 생각해야 할 거야. 이런 질문을 진지하게 생각하는 친구들이나 주위 사람들과 대화도 해 봐. 그리고 무엇보다 공책에 꼭 써. 한 번 쓰고 끝내지 말고, 나중에 읽으면서 혹시 헛점은 없는지, 덜 생각한 것은 없는지 고치고 다듬어 가길 바래. 그런 노력을 안보이면 수학의 세계도 자신만이 가지는 고유한 아름다움을 쉽게 안보여 줄지 몰라. 그리고 수학의 세계에만 있는 엄청나고 신비로운 힘을 나눠 주지 않을걸.

우리 선조들이 그런 수를 어렴풋하게 느낀 것은 오래 되었어. 그런데 그것을 자연수 만큼은 아니더라도 자연스럽게 받아들인 것은 얼마 안 돼. 자연수의 '반대편'이라는 것도 0 을 기준으로 해야 하잖아. 그래서 먼저 0 을 쉬이 받아들이는 문화에서 그런 수도 자연스럽게 받아들이는 게 당연하겠지? 지금 남은 기록으로 보면 역시 고대 인도에서 1,400 여 년 전에 0 의 반대편에 있는 수에 대해 지금 수준에 육박하는 생각을 했대. 그리고 인도 성과를 포함해서 여러 문명을 집대성한 아랍 문화에서는 그로 부터 몇 백 년이 지나서야. 물론 그들 이전에도 '0의 반대편에 있을지도 모르는 어떤 수' 를 상상하기는 했어. 2000여년 전 고대 중국, 1700여년 전 고대 그리스나 인도가 그런 수를 고민했던 흔적이 남아 있어 그러나 0 을 제대로 받아들이지 못하고 있었기 때문에 불완전했지. 곧 우리가 보겠지만 방정식이라는 것을 풀어가면서 잠시 임시로 빌려 오는 수단으로 주로 썼어. 이것에 대해서는 곧 이야기 해줄께.

앞에서 삼촌이 말했던 것들을 조금 자세히 보여줄까? 아래 그림들을 보자. 왼쪽부터 차례대로, 고대 중국, 2천 년이 넘은 '9장 산술(九章算術)' 이라는 책, 그 다음이 1700여년 전 인도의 기록, 이것은 자작나무 껍질을 파서 쓴 바흐샬리(Bakhshali) 원고야. 그 다음은 디오판테스의 '산술(arithmetic)' , 그리고 그 다음이 1400여년 전 인도의 브라흐마굽타의 책, 마지막으로 중세 아랍의 알-콰리즈미가 쓴 유명한 책 '메꿈와 균형' 들이야. 마지막 책은 하도 유명해서 그 저자 이름을 따서 '알고리듬'이라는 말이 보통 명사가 되었고, 그 책 제목의 일부가 '대수학(algebra;균형)' 라는 수학의 핵심 분야 중 하나를 지칭하는 말의 원조가 되었어. 워낙 오래되어서 아래 그림들은 원래 것들이 아니고 남아서 전하는 것들 중에 삼촌이 여기저기서 찾아 빌려온 거란다.

• 

  9장 산술

• 

  바흐샬리 원고

• 

  산술(라틴어 본)

• 

  메꿈와 균형

그런데 유럽에서는 '반대편의 수'를 받아들이기 더 힘들어 했던 것 같아. 앞의 편지에서도 말한 적 있지. 지금은 유럽이 수학의 강국들이지만, 수백년 전만해도 0 을 제대로 받아들이기도 쉽지 않을 정도였어. 그러니 그 '반대편의 수'야 말할 나위 있겠니. 파스칼 같은 위대한 수학자이자 철학자도

$0-4\ =\ 0$

이라고 했을 정도라니. 0 너머에는 있을 수 없으니까. 그래도 ' 0 - 4 는 있을 수 없다.' 라고 않고 0 이라고 한 것이 참 신기하구나. 아무튼 그 당시 그런 경향이 있었다고 해도 모두다 그렇게 생각한 것은 아니야. 그 당시, 그러니까 지금으로부터 한 3 백년 4 백년 전 쯤 유럽에서도 이미 그런 수가 '있고', 자연수 보다 못할 게 없다. 자연스럽게 받아들여야 한다는 주장이 오갔지. 결정적으로 그것에 기여한 사람은 데카르트야. 이런 사람들은 앞으로도 종종 걸어서 우리 앞으로 나올거야.

이 수들이 이상하게 여겨지는 건 당연하지. 없음에서 빼냈는데 무언가 있는 수라니 ! 하지만, 오랜 세월 전에는 이상하기만 했던 것이 세월이 지나면서 당연한 것으로 받아들여지듯, 지금 사람들에게는 이 이상한 수가 그다지 이상하지 않아. 분명히 있다고 받아들이지. 그렇다면 이제 수는 한쪽으로만 뚫리고 한 쪽은 0 으로 막힌 것이 아니라, 그 너머에도 있어. 예를 들어 이제는 이런 그림이 가능하지.

좋아, 있어, 있으니까, 다음은 ? 그것을 표현할 방법이 있어야겠지. 자연수도 이렇게도 표현하고 저렇게도 표현하며 어쩌면 오랫동안 경쟁했다가 결국 지금 우리가 쓰는 방식으로 정착했잖아. 그리고 셈들의 기호도 그랬어. 그렇듯, 이 수도 그래. 참, 이 수를 우리나라에서는 '음(陰)의 정수'라고 불러. 동양에서는 음과 양을 대칭으로 보니까 그랬을거야. 해는 양, 달은 음, 그래서 양력과 음력, 이런 식으로. 동양에서도 다른 나라에서는 '빚'을 뜻하거나 '부족' 을 뜻한다는 의미가 있는 다른 말로 부르기도 하고, 영어로는 negative number 라고 해. 다른 유럽어도 비슷해. 부정적이라는 뜻이 담겨 있어. 유럽에서는 실재로 이 수를 '악마의 기운이 깃든' 수로 봤을 정도라니까 이런 말을 썼겠지. 양의 정수는 자연수지. 그래서 양의 정수, 0, 음의 정수를 모두 합해서 그냥 정수(整數;integer)라고 불러.

아, 기호 이야기 해야지 ! 음의 정수를 나타내는 방법도 여러가지 였어. 그 중 대표적인 것이 자연수 앞에 + 를 붙여 썼다고도 해. 또는 그 수 위에 점을 찍거나. 이상하지? 지금은 - 를 붙이잖아.

$\dots ,\ -10^{10^{10}},\ \dots ,\ -10^{10},\ \dots ,\ -10^{3},\ -999,\ \dots ,\ -10^{2},\ -99,\ \dots ,\ -3,\ -2,\ -1$

로 쓰는 거지. 이렇게 쓰는 것이 가장 좋겠다고 해서 현대는 보통 이렇게 쓰고 있어. 왜 그럴까 ? 다음에 이것에 대해 말해보자. 오늘은 자연수와 0 말고도 새로운 수가 등장한 것만으로도 벅찰지 몰라. 이 수의 등장으로 이제 놀라운 일이 벌어져. 그리고 '새로운' 수가 나왔으니 이 수들 끼리 어떻게 셈으로 연결되는지에 대해서도 말해야겠지? 그런 이야기를 다음 편지에서 이어서 할께. 조금만 기다려 줄 수 있지?

자, 정리하면 이제 우리에게 수는 양쪽으로 뚫려 있게 되었어 ! 확실하게 구별하기 위해서 양의 정수인 자연수 앞에는 + 를 붙이고, 음의 정수에는 - 를 붙여 써 보면 이렇게 될거야.

$\dots ,\ -6,\ -5,\ -4,\ -3,\ -2,\ -1,\ 0,\ +1,\ +2,\ +3,\ +4,\ +5,\ +6,\dots$

이렇게 수의 공간이 확장되었는데, 이 광활한 세계에서는 과연 무슨 일이 이제 일어날까? 호기심을 가슴 가득 담고 기다려다오. 아니 오늘 편지 끝내기 전에, 스스로 한번 생각해보겠니?

음의 정수들에 대해서는 덧셈과 곱셈을 어떻게 할까? 왜 그렇게 하는 것이 옳다고 주장할 수 있을까? 음의 정수에 대해서도 뺄셈과 나눗셈은 덧셈과 곱셈을 거꾸로 하는 셈이라 하자. 그렇다면 어떻게 뺄셈, 나눗셈 하는 것이 옳을까?

오늘은 이만 쓸께. 어제 이 편지 쓰기 시작할 때는 비가 오고 안개가 꼈는데, 다 쓰고 난 지금은 보름이 살짝 지난 달이 하늘 높이 둥실 떠서 흐르는구나. 그럼 다음 편지에서 또 보자. 안녕 !

안개비를 걷어내고, 삼촌이 멀리 청사포구에서

수학 편지 대문으로.