NatNum Representation: 두 판 사이의 차이
(차이 없음)
|
2007년 3월 23일 (금) 23:25 기준 최신판
수의 표현
자연수란 하나, 둘, 셋, ... 이라는 우리 마음 속의 어떤 관념이다. 심상(心象)인 것이다. 그것은 아득한 그 무엇이지만, 성장하고 사회생활을 하면서 자연스럽게 우리 마음 속에 자리잡는다. 사람들은
- 나는 당신을 사랑합니다.
라고 간절한 마음을 드러내어 말로 한다. 그리고 저마다 익힌 언어로 이 말을 나타낸다. 말로 뜻을 전달한다. 어떤 민족들은 그 말을 쓸 수 있는 기호가 있고 어떤 민족들은 없다. 기호가 없으면 입으로 말하고 귀로 듣고 머리로 외우면서 뜻을 주고 받고 기억한다. 하지만 기호가 있으면 그 한계를 넘게 된다. 쓰고 보고 읽고 기록물로 저장한다. 수의 세계도 마찬가지다. '수'라는 관념도 기호로 나타내게 된다. 그 기호가 '숫자'다.
자연수가 우리에게 '있다.' 이제 그것을 나타내고 싶다. 그렇다면 어떤 기호를 가지고 어떻게 쓸 것인가 하는 문제로 넘어가게 된다.
- 기호? 그거 그냥 1, 2, 3, 으로 해서 열 둘이면 12로 하고, 예순이면 60으로 하고 ... 그러면 되는거 아냐?
라고 쉽게 마침표를 찍기 쉽다. 하지만 수학은 쉽게 마침표를 찍지 않는다. 모든 탐구가 그렇듯 수학도 물음표의 학문이다.
우리는 어려서부터 0 부터 9 까지 기호 10 개로 모든 자연수를 나타내는 '십진법'이라는 것에 익숙해졌다. 자연수를 나타내고 셈을 하는 것이 '너무나 간단해서 굳이 애쓸 필요 없는' 것이 된 것이다. 그러나, 이런 방식으로 수를 나타내기로 많은 사람들이 합의하고 덧셈 계산이 간단하게 된 것은 천 년도 한참 안되었으니 인류의 기나긴 역사를 돌이켜보면 최근의 일이라고 해도 과언이 아니다. 또한 지금의 방식이 가장 좋은 방법인지, 미래에도 과연 계속해서 이 방식을 쓸 것인지 장담하기 어렵다.
인류가 자연수를 나타내었던 여러 방법 중 몇 개를 보면서 그것들 안에 어떤 것이 다르고 어떤 것이 같은지 함께 짚어가자. 이것은 단지 역사적 고찰이 아니다. 이런 수기호 표현은 앞으로 수가 정수, 유리수, 실수로 확장되어 가고 다른 수학의 분야와 만나면서 매번 부딪히게 되는 문제다. 숫자 자체는 수를 드러낸 기호표현이라는 것을 잊어서는 안된다.
수 표현법
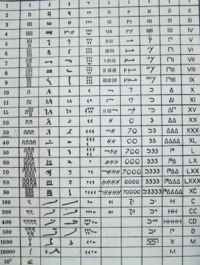
시대와 민족에 따라 자연수를 표현하는 방법이 달랐다. 문명이 교류해서 섞이면서 아라비아 숫자로 십진법으로 표시하고 세고 있는 민족이 많지만 소수 민족들 중에는 여전히 그들만의 셈하는 법이 있다고 한다. 고대 사람들의 수를 나타내어 셈하는 것을 모아 잘 들여다보면 저마다 다른 점도 있지만 그것들을 아우를 수 있는 어떤 공통점을 찾게 된다. 다시 말해 사람들은 다른 문명 속에서도 수를 나타내고 셈하는데 공통된 '규칙성'을 띄었던 것이다.
수의 표현이 기록으로 남은 것 중 가장 오래된 것은 B.C. 3000년 경 고대 이집트와 바빌론 문명의 자료라고 한다.
- 고대 바빌론에서는 '하나', '열', '예순' 과 같은 수를 나타내는 기호가 있었다.
- 마오리 족에게는 '하나'와 '열하나', 열하나들이 열하나인(십일의 제곱), 그리고 십일의 세제곱에 해당하는 수를 나타내는 기호가 있었다.
- 고대 로마에서는 '하나'를 'I','다섯'을 'V', '열'을 'X', '오십'을 'L', '백'을 'C', '오백'을 'D' '천'을 'M' 로 표시했다. 이 기호는 지금도 유럽에서 '몇 년'을 나타낼 때 쓰곤 한다.
다시 말해, 저마다 '하나'를 나타내는 기호는 있었고, 그것을 반복해서 어느 정도까지는 쓴다. 그 다음 문명권 마다 다르지만 기호 하나가 '하나를 여러 개' 나타내는 새로운 기호를 쓰고 그것과 하나의 기호를 결합해서 수를 이어가고, 그러다가 또 어느 정도 가서 새로운 기호가 등장하고 그 앞의 기호들과 결합해간다. 이런 과정이 반복된다. 차이는 '몇까지 세다가 새로운 기호가 나오느냐' 이지만, 공통적으로 그런 법칙은 따랐다. 그런 과정에서 가장 폭넓게 쓰였던 수 표현 방법들을 예로 더 깊이 들어가보자.
더하기 법
자연수를 나타내는 기호는 달랐다. 새로운 기호가 등장한다는 것은 기호들끼리 새로운 결합 방식이 있다는 것을 의미한다. 나름의 법칙에 따라 '수'를 나타내었다. 이렇게 기호와 기호를 결합하는 법칙에 따라 다른 수표현 체계(System)를 가지게 되는 것이다. 예를 들어 고대로마에서 '백.십.팔'을 나타내는 기호로
- CXVIII
를 썼다. 그리고 과 지금 우리식으로 하면 '2019' 를
- MMXIX
로 쓴다. 두가지 법칙이 적용된 것을 알 수 있다.
- 큰 수를 나타내는 기호를 먼저 쓰고 작은 수를 나타내는 기호는 나중에 쓴다.
- 예외적으로 만약 작은 수가 큰 수 앞에 나오면 둘 사이의 차로 나타낸다. 예. IV는 '넷'을 IX는 '아홉'
- 앞의 예외적인 경우를 고려하여 정리한 다음 모두 더하기 한 결과가 그 수다.
앞에 썼던 예를 보면, 큰 수 부터 쓰고
- C (백) + X(십) + V(오) + III (하나 + 하나 + 하나)
- M(천) + M(천) + X(십) + IX(구)
예외적으로 IX(구)를 나타낼 때, V(오) IIII 이 아니라 X(십)에서 하나 빼기 IX 를 쓴 것이다.
이처럼 표현한 기호들을 '붙여서 늘여쓰고 더해서' 그 결과로 나타낸 것이다. 이런 방식을 더하기 표현법(additive notation) 이라고 부를 수 있다.
이 수표현은 기호가 7개 밖에 안되고 법칙도 간단해서 그럴 듯해보인다. 그렇지만 십, 백, 천, 만, ... 과 같이 수단위가 올라갈 때마다 기호가 덧붙여져야하기 때문에, 자연수가 무한개라는 점까지 생각을 않더라도 지구의 길이, 원자의 개수를 나타내는 문제들을 생각해보면 이 표현법이 상당히 불편할 것이라는 것을 알 수 있다. 또한 이 표현법은 그 셈을 하는데도 복잡할 수 밖에 없다. 지금의 우리에게는 아주 간단해 보이는 계산을 해보자. '백십팔 더하기 이백구 더하기 삼' (직접 해보라.)
- CXVIII + CCXI + III
더하는 수가 많아지거나 수가 커질수록 계산은 무척 복잡해진다. 뺄셈과 나눗셈은 생각않더라도 곱셈의 복잡성만해도 무척 클 것이라는 것은 두말할 나위없다. 지금의 우리에게는 초등학생도 계산할만한 문제를 이런 식으로 수를 표현을 사용한 시대에는 극소수의 전문가들만이 할 수 있었다고 한다. 따라서 '계산'은 소수의 전문가'들이 독점하는 지식의 범주였다. 따라서 우리 대부분에게 '자연스러운' 수와 그 셈이 당시에는 극소수들이 나누는 지식이었고 보통 사람들에게는 '신비한' 어떤 것이었을 것이다.
자릿수법
앞의 고대 로마 기호들은 예외를 빼고나면 '어느 자리에 있건 상관없이' 고유한 수를 나타냈다. 그런데 모든 문명의 수표현이 그것을 고집한 것은 아니다. 당장 지금 우리가 쓰는 방법을 보자.
- 111
에서, 첫번째 1과 두번째 1과 세번째 1이 모두 '다른 수'를 나타낸다. 첫번째 1은 백을 두번째 1은 열을 마지막 1은 하나를 나타내는 것이다. 물론 이 방법에서도 위의 방법처럼
- 큰 수를 앞에 쓰고,
- 고대 로마와 같은 예외 조항 없이
- 세 '수'를 더해가는 것이다. 다만 '같은 기호를 써도 자리마다 뜻하는 수가 다르다.
이처럼 같은 기호가 자리에 따라 다른 수를 나타내기도 하는데, 이를 자릿수법(positional notation)이라고 부르자. 우리에게 가장 익숙한 십진법(decimal)에서는 '없음' 부터 '아홉'까지는 모두 다른 기호를 쓴다. 우리에게 가장 익숙한 아라비아 숫자의 경우
- 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
열 개를 사용하고 다른 자리에 있을 때마다 다른 의미를 갖는다. 같은 얼굴을 해도 자리에 따라 다른 사람이 되는 것 처럼.
따라서, 우리가 쓰는 수 표현(십진법 아라비아 숫자 체계)에서 규칙성을 뽑아 정리해보면 이렇다.
- 제일 왼쪽에는 0 을 쓰지 않는다.
- 처음 오른쪽 n 번째 자리에 있다면 그 숫자에 '십'을 n 번 곱한 만큼의 수를 나타낸다. 가장 오른쪽은 0 번째 그 다음은 1 번째로 약속한다.
- 예를들어 231 의 경우 : 1 이 뜻하는 것은, 110^{0}, 3 은 3 10^{1} , 2 는 2 10^{2}
- 그 수를 모두 '더하기'해서 수를 나타낸다. 앞의 예에서 200 + 30 + 1 = 231.
이런 십진법 아라비아 숫자 체계가 하루 아침에 이루어진 것은 물론 아니다. 그 이전에도 다른 기호와 다른 법칙을 적용하여 '자릿수 법'으로 나타내기도 했다. 10 진법이 아닌 수 세는 단위를 가진 민족도 많았다. 10 진법을 썼던 문명에서 기호로 아라비아 숫자를 썼던 것도 아니다. 오랜 동안 문명들 끼리 어울리면서 도달한 것이다. 그 획기적 전기를 마련한 수가 0 이다. '영' 을 수로 인식하고 '0' 이 숫자로 정착했던 것은 인류 문명사에 커다란 획을 긋는 사건 중 하나다. 이렇게 아라비아 숫자 십진법 체계가 지금과 같이 되는데는 한 때 문화의 꽃이 만개하였던 고대 인도의 철학과 중세 아랍 문화의 산물이다. 최소한 5 세기 경에는 인도에서 0을 나타내는 숫자가 사용한 증거가 있고 유럽에는 10세기부터 13세기 동안 수백년에 걸쳐 마침내 정착하게 된다. 이때 유럽은 당시 경제 문화적으로 융성했던 아랍에서 책을 번역하여 발달한 문명을 받아들였다. 아랍은 고대 그리스의 성과를 번역하면서 그 문명의 성과를 이어받아 수학을 발달시켰다. 이렇듯, 오랜 세월 서로 다른 문명들이 교류하는 동안, 덜것은 덜어내고 새로 만들 것은 만들어왔다. 그 결과 마침내 우리는 온지구를 덮어버릴 만큼의 쌀알갱이들의 개수를 나타내는데 몇 초면 충분히 쓸 수 있는 시대에 살게 된 것이다. 충분히 짐작할 수 있다시피 이 체계는 덧셈과 곱셈의 계산도 무척 효율적이다.
그렇다고 해서, 십진법이 가장 좋은 체계라고 말할 수 있을까? (이에 대해서 역사적 자료와 의미를 자세히 알아본다는 것은 그 자체로 두터운 책의 제목이 될 수도 있다. 여기서는 '필요한 부분만 가볍게' 훑어보기로 한다.)
수표현 체계의 일반화
고대 로마의 경우 하나의 단위, 다섯 단위 열 단위... 에 새로운 기호들이 등장했다. 다만, 숫자가 들어가는 자리가 기본적인 역할을 하지 않았다. 다른 시대 다른 민족에서는 '자릿수'가 본질적으로 중요한 역할을 하게 된다. 자릿수 표현법의 장점은 아무래도 적은 기호로 큰 수를 나타낼 수 있다는 점이다. 문명이 발달할수록 '큰 수'에 대해 표현해야할 일이 많아졌을 것이다. 따라서 자릿수가 중요한 역할을 하지 않은 고대 로마 체계와 같은 수표현은 점점 더 많은 기호를 가져야 한다. 한계를 가질 수 밖에 없다. 그에 비해 자리가 중요한 역할을 하게 되면, 몇 개의 기호만으로 큰수도 표시할 수 있다. 이제 우리가 현재 많이 쓰고 있는 '더하기-자릿수 법'에 관심을 집중한다. 이를 통해 지금 앞으로 만나게 될 '수와 그 표현'의 밑바닦에 어떤 법칙들이 관통하고 있는지 이해할 수 있다.[1]
앞에서는 최대한 줄여서 두 개의 수 표현 방법만 보았고 그것을 통해 성급하긴 했지만, 규칙성을 내세워보았다. 이제 그 규칙성을 '틀어서' 과연 그 안에서 어떤 성질이 있는지 요모조모 살펴 볼 차례다. 익숙한 십진법 체계로부터 거슬러 올라가보자. 앞에서 십진법 체계를 이야기 할 때 그 '법칙'에 대해서 썼던 것을 현대적 표현 방식으로 하면 다음과 같이 할 수 있다. 예를 들어 111 의 경우[2],
여기서 잠시, 곱셈은 * 로, 덧셈은 + 로 쓰기로 한다.
이것이 만약 십진법 체계가 아니라 일곱 개의 기호만 있는 칠진법 체계라면? 영, 하나, 둘, 셋, 넷, 다섯, 여섯 까지 세고, '일곱' 이라는 관념을 표현하기 위해서는 자리를 하나 올려 써야 한다. 다시 말해 영, 하나, 둘... 을 나타내는 기호가 차례대로 a, b, c, d, e, f, g 라면, 일곱이라는 수를 나타내는 숫자는 'ba' 가 될 것이다. 그 다음은 bb, bc, bd, .. 로 세어가게 된다. 그러다가, 열 셋이라는 수는 bg 라는 '숫자'로 나타난다. 그렇다면 열 넷은 ? 이제 자리수가 한자리 더 올라가야 한다. baa. 이어서 열다섯은 bab. 요약하면
- 영 a , 하나 b , 둘 , ..., 일곱 ba , ... , 열하나 be, 열둘 bf, 열셋 bg , 열넷 \mapsto baa , 열다섯 bab , ...
물론 한글로 나타낸 '수'의 개념에도 벌써 '십진법'의 관념이 투영되어 있긴 하다. 하지만 12진법의 흔적이 남아있는 영어로 해보면[3]
- zero a , one b , two 셋, ..., seven ba , ... , eleven be, twelve bf, thirteen bg , fourteen baa , fifteen bab , ...
자, 만약 7 진법의 기호를 0,1,2,3,4,5,6 이라면? 그때의 111 이라는 숫자는 10 진법으로 부르기 위해 '번역' 하면
가 된다. 처음 자리 1 은 일곱이 두번, 다음 자리 1 은 일곱이 한 번, 그리고 마지막 1 은 그대로 1이다. (일곱이 0 번 나온다.) 따라서 이 수는 '오십칠'의 수를 나타내고 만약 십진법으로 바꾼다면 '57'로 쓰게 된다.
이런 식으로 자릿수법의 표현 체계를 변수를 이용하여 보다 일반적인 식으로 나타내면 어떤 자연수 z를 로 표현하고 이것이 십진법 이라면
이고 만약 7진법이었다면
이다. 위의 숫자 111을 2진법으로 나타내어 졌다면 어떤 '수'를 표현하겠는가?
다. 따라서 수 '일곱'을 나타내고 십진법으로 표현하면 7, 기호로 0,1,2, ... 6 을 쓰는 7진법으로는 10 으로 쓴다.
자 이제 보다 일반적인 식으로 '수표현 체계'를 정리해 볼 때가 되었다. 어떤 자연'수' z 가 q 진법으로 로 나타내보자.
이때 부터 까지 어떤 자연수에 에 대해서건 는 보다 크거나 같고 보다 작거나 같은 자연수다. 앞 절에서 본 '규칙성'에 따라 은 첫번째 자리에 오는 숫자이므로 0 이 아닐테고.
- 현대의 컴퓨터는 2진법을 쓴다. 2진법을 쓴다는 것은 나타내는 기호가 두 개 있게 될 것이다.
- 고대 바빌로니아 에서는 60진법을 썼다. 지금까지도 그런 흔적은 남아있다. 초, 분, 시를 계산할 때는 여전히 60진법을 쓰고 있다.
- 수를 사용하는 예를 유심히 관찰하면 이렇게 다양한 진법이 남아 있다는 것을 우리 일상에서 여러 곳에서 발견할 수 있다. 스스로 여러 예를 찾아보라.
- q-진법에 대한 다양한 예
일반식의 몇가지 문제
10진법이든, 7진법이든 상관없이 q-진법으로 어떤 자연수 z를 나타내는 일반식을 유추해보았다. 잠시 멈춰 서자. 처음에 우리는 어떤 질문을 던졌던가? 우리가 궁금해 했던 것이 무엇이었던가? 그것은 다름아닌 '자연수를 어떻게 기호로 표현할 것인가?' 였다. 방법은 많을 수 있지만, 그 중 '기호 q 개로 더하기-자리수법'을 쓴, q-진법으로 나타내는 방법에 집중한 것이다. 그렇다면 짚고 넘어가지 않으면 안되는 문제들이 있다.
- 어떤 자연수에 대해서도 q를 무엇을 쓰건 'q-진법체계'로 그 자연수를 나타낼 수 있을까 ?
다시 말해, q-진법은 모든 자연수를 다 표현할 수 있단 말인가? 다 표현 못한다면 우리의 다음 발길은 정해진다. 과감하게 q-진법을 버리고 발길을 돌려 원점으로 돌아가 다시 시작하는 것, 또는 무엇을 표현할 수 있고 무엇을 표현할 수 없는지 따져들어가 문제를 해결하는 길. 다행히 모든 자연수를 표현할 수 있다면 아주 좋다. 아직까지는 잘 온 거다. 그러나 종점은 멀었다. 모든 자연수를 표현할 수 있다 하자. 그럴 때, 자연수 하나에 q 진법으로 나타낸 기호(숫자)가 딱 하나인가 아닌가 답해야 한다. 왜 ? 어떤 자연수 하나에 숫자가 둘 이상이거나 기호 하나에 자연수 둘 이상을 나타내는 경우를 나름대로 상상해보라. (정말로 상상해보라. 어떤 일이 일어날까?) 다시 말해
- 서로 다른 자연수는 반드시 다른 숫자로 표현될까?
앞의 두 문제를 한 문장으로 '일대일 대응[4]' 개념을 써서 표현하면 다음과 같다.
- 어떤 'q진법체계'와 자연수는 일대 일로 대응할까 ?
이 문제에 대한 답은 별 문제가 안된다는 것을 어렵지 않게 짐작할 수 있다. q-진법을 세운 규칙을 보면 충분하다. 자연수란 하나 하나 커져가는데 q 진법에는 최소한 하나를 표현하는 방법이 있다. 그리고 2 진법이나, 3진법이나, ... , 10진법이나 11진법이나, 12진법이나, ... , 60진법이나... 어떤 것인건 자리수를 하나 올리는 '계단'이 언제 나오느냐의 차이일 뿐 본질적으로, 하나 더 큰 수, 하나 더 큰 수를 표현하는 방법이 분명히 존재하기 때문이다. 게다가 그 기호는 다르도록 만들었다.
아주 좋다. 그렇지만, 여전히 종점은 아니다. (사실 수학 세계에서 종점은 없어보인다.) 다음 가능한 최우선의 질문은 이렇다.
- q-진법체계에서 p-진법 체계로 전환하는 알고리듬이 있을까?
앞으로 보완될 내용
- 앞의 질문에 대한 증명 : Horner Scheme(우리나라에서는 보통 '나머지 정리'라고 부른다)를 이용하여 증명할 수 있다.
- 이 쪽 진법 체계의 기호를 저 쪽 진법 체계의 기호로 통역해주는 웹상의 프로그램이 있다.
- 2진법에서 36진법까지 웹상에서 바로 바꾸워주는 프로그램 을 참고 하라.
- 'q-진법'의 응용 예제 : 봉투는 몇 개나 준비할까? 무게를 재기 위해 추는 몇개나 올릴까?
- 하나의 진법에서 다른 진법으로 변환하는 알고리듬 에서 정리 중: 예
- 해밍코드(Hamming code,Коды Хемминга)
- 진법의 확장 : 정수 유리수, 실수로.
Note
- ↑ 수를 표현해오던 방식이 어떠했는지 두루 살피는 것은 많은 자료와 역사적인 고찰이 필요하다. 고대에는 문명권마다 수 표현이 달랐다. 어쩌면 수 표현을 기준으로 문명권을 묶어 연구해볼 수도 있겠다. 아주 흥미로운 주제인 듯...
- ↑ (만약 이 지수로 나타내는 표현이 익숙하지 않다면 지수 연산 부분 참고)
- ↑ 사실 언어마다 독특한 진법 체계의 흔적이 남아 있다. 프랑스어에서는 이십진법의 흔적이 남아 있다. 이십에 특별한 말인 vingt 가 있고, 예를들어 팔십은 quatre-vingts,(20이 네개) 라 한다.
- ↑ 일대일 대응의 정확한 정의에 대해서는 함수 이야기 를 참고하라. 간단히 말하면 대응하고자 하는 대상들 '전부'를 대응시켜야 하고, 대응시키려는 대상이 다르면, 대응되는 값도 다르도록 대응 규칙을 정한다는 뜻이다.
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia















