Pythagor Tri Num: 두 판 사이의 차이

2007년 11월 13일 (화) 20:20 기준 최신판

자연수의 세계 로 돌아가기

피타고라스 세쌍수

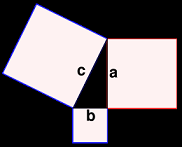
아래 일명 '피타고라스 정리'라고 부르는 기하학적 정리에 대하여 익숙하다.

피타고라스 정리 : 직각삼각형의 빗변을 한 변으로 하는 정사각형의 면적은 다른 두 변을 변으로 하는 정사각형들의 면적의 합과 같다.

이 정리는 피타고라스 이전 바빌론, 이집트, 중국과 같은 다른 고대 문명권에서 실생활에 쓰이고 있었던 것으로 알려진다. 이 정리를 다시 말하면 어떤 삼각형의 세 변의 길이가 a, b, c 일 때,

c가 빗변인 직각삼각형이면,

a^{2}+b^{2}=c^{2}

이다. ^[1]

이 정리에서 보듯 위의 특별한 등식 관계를 갖는 세 수에 촛점을 맞추면 흥미로운 사실들을 찾을 수 있다.

정의

앞에서 변의 길이를 '자연수'로 제한해보자. 그렇다면 피타고라스 정리와 그 주석에서도 말했다시피 '자연수 길이인 세 변을 갖는 직각삼각형은 모두 몇 개나 되고 그 성질들은 무엇일까?' 하는 기하학적인 문제는 ' $a^{2}+b^{2}=c^{2}$ 이 참이도록 하는 자연수의 세 쌍 (a,b,c) 찾기'라는 산술 문제와 다를 바 없게 된다.

정의 :

a^{2}+b^{2}=c^{2}

이 참이도록 하는 자연수의 세묶음 (a,b,c)을 피타고라스 세쌍수라 한다.

여기서는 쓰기 편하게 간단히 세쌍수라고 부르기로 하자. 예를 들어 우리에게 가장 익숙한 세쌍수는 (3,4,5)가 있다. 그리고 (7,24,25), (15,36,39)도 되는데 이 수는 지금으로부터 2500여년 전 고대 인도의 문헌에서 발견되었다고 한다. 그렇다면 과연 몇 개나 있을까?

성질 : 세쌍수는 무수히 많다

(3,4,5)가 세쌍수라면 그 수들의 어떤 자연수 k든 그 배수들은 모두 세쌍수가 된다는 것은 분명하다 : $(3k)^{2}+(4k)^{2}=(5k)^{2}$ 이기 때문이다. 이는 세쌍수가 끝없이 많다는 것을 말해준다. 이건 너무 뻔해서 흥미롭지 않다. 위의 예에서 공통약수를 모두 나누고 나머지들만으로 표현하면 (3,4,5), (5, 12, 13), (7,24,25) 가 된다. 이런 수들을 나열해보면

(3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53) , ...

그렇다면 이렇게 서로 공통인 약수가 없는 '세쌍수'는 몇 개나 될까. ^[2] 어떻게 그것을 알 수 있을까?

첫번째 시도
세쌍수의 조건을 다시 쓰면

c^{2}-b^{2}=a^{2}

이므로 두 제곱 수의 차가 제곱이 나오는 경우를 모두 뽑아보면 될 것도 같다. 제곱수를 나열하면

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121,144, 169, 196, 225, 256, 289, ...

이다. 두 수들의 차이를 보면,

3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, ...

차이만 나타내는 수의 열은 모두 2씩 커져간다. 이는 우연이 아닌데, 왜냐하면 이를 식으로 표현해보면 $(n+1)^{2}-n^{2}=2n+1$ 이고 n이 1증가할 때마다 2씩 증가하게 되기 때문이다. 여기서 $2n+1$ 은 모두 홀수인데 이 꼴의 수 중에서 제곱인 수가 있다면 그것은 세쌍수가 될 것이다. 9, 25, 49, ... 과 같은 수들이다. 그렇다면 이 수들

(2n+1,n^{2},(n+1)^{2})

은 '공통약수가 없는' 세쌍수가 될 것이다. (왜 그런가?) 홀수의 제곱은 항상 홀수인 제곱수이므로 공통약수가 없는 세쌍수가 끝없이 많다. 앞에 나열한 것들 중 이런 수들만 진하게 표현해보면

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53)

하지만 이런 세쌍수들이 모든 세쌍수를 나타내기에는 턱없이 부족하다는 것을 위에 나열한 세쌍수의 예에서만 봐도 금방 알 수 있다. '모든 세쌍수'를 나타내기에는 아직 멀었다.

두번째 시도

앞의 예에서 이웃하는 두제곱수가 아니라 한칸 건너 수들의 차이를 보자.

8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, ...

다.

(n+2)^{2}-n^{2}=4n+4

이므로 차이는 모두 4다. 그렇다면 4n+4가 제곱수가 되는 꼴만 찾으면 되는 것이다. 이 방법을 쓰면 앞의 첫번째 시도에서 찾지 못한 세쌍수를 찾을 수 있을까? 스스로 검토해보고 일반적으로 보여보라.

두 번째 시도에서 공통약수가 없는 새로운 세쌍수를 더 추가했다고 해서,그리고 그 차이를 두 칸 건너 해본다고 해서, 우리가 처음 던진 질문 자연수 길이를 갖는 직각삼각형 모두를 찾는 다시 말해모든 세쌍수를 찾는 일반적인 방법이라 하기 어렵다. 이 방법을 알고리듬이라 할 수 있을까?

세쌍수를 만들어내는 알고리듬

어떤 조건을 갖는 두 수로 얼마든지 세쌍수를 만들어낼 수 있다.

정리 : u > v 인 두 자연수가 아래의 연산을 한 세 결과값 a, b, c는 세쌍수를 이룬다.

a={\frac {u^{2}-v^{2}}{2}},

b=u\cdot v,

c={\frac {u^{2}+v^{2}}{2}}.

이를 검토하는 것은 어려운 일이 아니다. 왜냐하면

\left({\frac {u^{2}-v^{2}}{2}}\right)^{2}+(u^{2}-v^{2})^{2}=\left({\frac {u^{2}+v^{2}}{2}}\right)^{2}

를 보이면 되기 때문이다.

이것은 아직 우리의 목표에 이른 것이 아니다. 우리의 목표였던 공통약수가 없는 모든 세쌍수를 찾는다면 위의 식은 엉성하다. 당장 입력 값 u, v가 공통 약수를 갖는다면 a, b, c도 공통약수를 갖게 된다는 것을 놓치면 안된다. 그리고 만약 u, v가 둘다 홀수면 a, b, c가 2의 배수로 공통 약수를 갖게된다.

정리 : u > v 인 두 자연수가 모두 홀수이고 공통약수를 갖지 않는다면, 아래의 연산을 한 세 결과값 a, b, c는 공통 약수를 갖지 않는 세쌍수를 이룬다.

a={\frac {u^{2}-v^{2}}{2}},

b=u\cdot v,

c={\frac {u^{2}+v^{2}}{2}}.

이는 이 알고리듬을 통해서 나온 세 수 a,b,c가 공통약수 없는 세쌍수를 이룬다는 것을 말한다.^[3] 그렇게 '공통약수'문제를 피해간다고 해도 문제는 '모든' 세쌍수를 찾는 알고리듬인가 하는 문제는 여전히 남아 있다.

공통약수를 갖지 않는 '모든' 세쌍수를 표현하기 위해서는 그 역을 증명해야만 한다. 다시 말해

정리 : a, b, c는 공통 약수를 갖지 않는 세쌍수를 이룬다면, 모두 홀수이고 공통약수를 갖지 않는 두 자연수로 u, v (이때 u > v)된 위의 식을 얻을 수 있다. ^[4]

자, 남은 일은 증명 밖에 없다. 임의의 세쌍수 (a,b,c)가 있다고 하자. 그러면

a^{2}+b^{2}=c^{2}

이다 (주의 : a, b 는 동시에 짝수일 수 없다는 것은 '공통약수 없는 세쌍수 기준에 볼 때 당연하다. 그런데 둘 다 홀수일 수도 없다. 왜 그런가?). 일반성을 헤치지 않으므로 a를 홀수, b를 짝수라 하자. 그러면

a^{2}=c^{2}-b^{2}=(c+b)(c-b)

이다. 그래서 c+b = m이고 , c -b = n인 자연수가 된다. 이를 a, b, c의 관점으로 정리하면

a={\frac {m-n}{2}},

b^{2}=m\cdot n,

c={\frac {m+n}{2}}.

이다. 다음을 스스로 검토해보라.

m과 n은 홀수다.
m과 n은 공통약수를 갖지 않는다.
$b^{2}=m\cdot n$ 이고 m과 n이 공통약수를 갖지 않으면 m도 n도 어떤 수의 제곱꼴이다.

증명끝.

?

두 수가 아니라 하나의 수로 생성 알고리듬을 만들어내는 것은 가능할까?
공통약수가 없는 모든 세쌍수가 아니라, 조건을 까다롭게 해서
- 연속하는 두 수가 세쌍수에 포함되는 세쌍수는 끝없이 많을까? 예 : (3,4, 5), (7, 24, 25), (9, 40, 41), ...
- 세쌍수의 세 수 중 하나는 완전제곱수가 되는 세쌍수는 끝없이 많을까? 예 : (3,4,6), (7, 24, 25), (9, 40, 41), ...
- 세쌍수의 세 수 중 두 수가 완전제곱수가 되는 세쌍수는 ?
(페르마 문제) : a + b 와 c가 완전 제곱수인 세쌍수는 ?
직각이 아닌 변의 길이가 같은 정수 길이를 갖는 직각 삼각형이 있다고 하자. 예: (5, 12,13)과 (9, 12, 15)) 그렇다면 같은 변을 붙이면 새로운 삼각형을 얻는다. (앞의 둘을 붙이면 (13,14,15)인 삼각형을 얻는다.) 이런 삼각형을 자연수 헤론삼각형 ^[5]이라 부르자. 모든 자연수 헤론 삼각형을 얻는 알고리듬은?
직각 삼각형은 작은 두 각의 합이 90도가 되는 삼각형이다. 그렇다면 어떤 삼각형에서 두 각의 차가 90도가 되고 세 변의 길이가 자연수인 삼각형을 모두 찾는 방법은?
직각 삼각형은 한 변이 60도이고 세 변의 길이가 자연수인 삼각형을 모두 찾는 방법은?
사각형으로 확장한다면, n 각형으로 확장한다면?

Q

직각 삼각형의 세 변이 자연수라면 그 면적은 6의 배수고, 세 변의 길이의 곱은 60의 배수다.
다음 문제를 풀어보시오.

소수의 분포에서도 살짝 비췄지만, 4n+1 꼴이 되는 수와 4n+3의 수는 겉으로보기에는 별 차이 없어보이는데, 두 집합 사이에는 이상스런 차이들이 있다.

\{x\ |\ x:=4\cdot n+1\ ,\ n\in \mathbb {N} _{0}\}=\{1,5,13,17,21,25,29,33,37,\cdots \}

\{x\ |\ x:=4\cdot n+3\ ,\ n\in \mathbb {N} _{0}\}=\{3,7,11,15,19,23,27,31,35,\cdots \}

이다 여기서 소수만 남기면

4n+1 꼴에서는 : 5, 13, 17, 29, 37, ...
4n+3 꼴에서는 : 3, 7, 11, 19, 23, 31, ..

여기서 주목할 수 있듯, 4n+3꼴 소수는 그렇지 않은데, 4n+1꼴 소수는 피타고라스 세쌍수의 빗변이 된다. 과연 항상 그럴까? 거꾸로, 만약 피타고라스 세쌍수에서 빗변이 소수로만 되어 있다면 그런 세쌍수의 소수들은 모두 4n+1을 가지고 있을까?

Note

↑ 그 역도 성립한다 : $a^{2}+b^{2}=c^{2}$ 이면 이 삼각형은 c 를 빗변으로 하는 직각삼각형이다. 이렇게 표현할 때, 피타고라스 정리가 기하학적 문장과 대수적 문장을 연결 짓는다는 것을 더 분명하게 알 수 있다.
↑ 사실, 세쌍수 중 아무거나 두 수가 공통약수를 갖으면 세 수 모두 공통약수를 갖는다. 따라서 세 수가 공통약수를 갖지 않는다는 것을 보이기 위해서는 두 수가 공통약수를 갖지 않는다는 것만 보이면 된다. 왜 그럴까?
↑ 집합의 용어로 하면
$\{(a,b,c)\ |\ a=f(u,v),\ b=g(u,v),\ c=h(u,v),\ ;(u,v)=1\ ;u,v\in {\mbox{Odd}}\}\subseteq {\mbox{Phyth-Triple }}$
이때 f, g, h는 위의 식이다.
↑ 이를 증명하면
${\mbox{Phyth-Triple }}\subseteq \{(a,b,c)\ |\ a=f(u,v),\ b=g(u,v),\ c=h(u,v)\ ;(u,v)=1,u,v\in {\mbox{Odd}}\}$
을 보임으로써 결국 우리의 목표에 이르게 된다.

↑ 디오판테스의 '산술'의 그리스어판을 라틴판으로 번역한 Bachet 는 그 책에 몇 개의 흥미로운 문제를 던졌다. 여기에 헤론삼각수를 언급했다. Web자료 중 그와 관련된 부분을 옮긴다. 원문

Bachet also worked on number theory. He is most famous for his Latin translation of Diophantus's Greek text Arithmetica (1621) in which Fermat wrote his famous 'Last Theorem' marginal note. In fact the work contains relatively little original material by Bachet who based his text on the problems of Diophantus which appeared in Bombelli's Algebra and on a complete Latin translation by Wilhelm Holzmann (also known as Xylander) in 1575. Let us note, however, one of the problems which Bachet gives in his translation:

  9. Find a triangle with rational sides and a rational altitude.

Such triangles, called Heronian triangles, also have rational area. Notice that from an Heronian triangle one can always obtain a triangle with integral sides and integral area.

바쉐(Bachet)의 디오판테스 '산술' 번역작업은 수론의 중요한 몇개의 문제와 연관되어 있다. 라그랑쥐 정리 와 페르마-오일러 정리를 참고하라.

[1] 그 역도 성립한다 : $a^{2}+b^{2}=c^{2}$ 이면 이 삼각형은 c 를 빗변으로 하는 직각삼각형이다. 이렇게 표현할 때, 피타고라스 정리가 기하학적 문장과 대수적 문장을 연결 짓는다는 것을 더 분명하게 알 수 있다.

[2] 사실, 세쌍수 중 아무거나 두 수가 공통약수를 갖으면 세 수 모두 공통약수를 갖는다. 따라서 세 수가 공통약수를 갖지 않는다는 것을 보이기 위해서는 두 수가 공통약수를 갖지 않는다는 것만 보이면 된다. 왜 그럴까?

[3] 집합의 용어로 하면
$\{(a,b,c)\ |\ a=f(u,v),\ b=g(u,v),\ c=h(u,v),\ ;(u,v)=1\ ;u,v\in {\mbox{Odd}}\}\subseteq {\mbox{Phyth-Triple }}$
이때 f, g, h는 위의 식이다.

[4] 이를 증명하면
${\mbox{Phyth-Triple }}\subseteq \{(a,b,c)\ |\ a=f(u,v),\ b=g(u,v),\ c=h(u,v)\ ;(u,v)=1,u,v\in {\mbox{Odd}}\}$
을 보임으로써 결국 우리의 목표에 이르게 된다.

[5] 디오판테스의 '산술'의 그리스어판을 라틴판으로 번역한 Bachet 는 그 책에 몇 개의 흥미로운 문제를 던졌다. 여기에 헤론삼각수를 언급했다. Web자료 중 그와 관련된 부분을 옮긴다. 원문

Bachet also worked on number theory. He is most famous for his Latin translation of Diophantus's Greek text Arithmetica (1621) in which Fermat wrote his famous 'Last Theorem' marginal note. In fact the work contains relatively little original material by Bachet who based his text on the problems of Diophantus which appeared in Bombelli's Algebra and on a complete Latin translation by Wilhelm Holzmann (also known as Xylander) in 1575. Let us note, however, one of the problems which Bachet gives in his translation:

9. Find a triangle with rational sides and a rational altitude.

Such triangles, called Heronian triangles, also have rational area. Notice that from an Heronian triangle one can always obtain a triangle with integral sides and integral area.

바쉐(Bachet)의 디오판테스 '산술' 번역작업은 수론의 중요한 몇개의 문제와 연관되어 있다. 라그랑쥐 정리 와 페르마-오일러 정리를 참고하라.

[1]

[2]

[3]

[4]

[5]