Steiner Net

이 page는 앞으로 많이 보태질 계획입니다. 누구나 글을 쓸 수 있습니다. 정성을 모아주십시오. ( 수학식 쓰기)

MaxMin 문제 - 들아가는 말 로 돌아가기

Steiner Network 이런 상황을 함께 상상해보자.

네 마을이 있다. 예전에는 이 마을들을 잇는 길이 없었다. 그런데 세월이 지나면서 네 마을 사람들이 교류가 활발해졌다. 서로 친하게 지낼 일도 많아지고 물건을 옮겨야 할 일도 많아졌다. 마침내 네 마을의 촌장들이 모여 이 네 마을을 잇는 길을 만들기로 했다. 어떻게 만들어도 좋은데 이 길을 통해 한 도시에서 다른 도시로 갈 수 있게만 하면 된다. 어떻게 잇는 길이를 최소로 할 수 있을까?

문제를 단순하게 하기 위해 먼저 이 마을들이 정사각형이루는 점들에 자리하고 있다고 가장한다.

(쉬타이너 문제) : 주어진 점이 k 개 있다. 어떻게 하면 이 k 개 점을 모두 잇되 길이를 가장 짧게 할 수 있을까?

쉬타이너 문제의 답은 쉬타이너 망이다

다음의 조건을 충족하는 망(network)을 쉬타이너 망이라 부르기로 하자.

모든 꼭지점들은 선분 들로 이루어져 있다.
하나의 꼭지점에서 뻗어나간 어떤 두 선분이 이루는 각은 120도 보다 작지 않다.^[1]
두 개의 선분이 뻗어 나올 경우 이들이 이루는 각은 120도 보다 크거나 같다. 만약 세 개의 선분이 뻗어 나올 경우 이것들 사이의 각은 120도다.

정리 : 쉬타이너 문제를 해결하는 기하적 도형은 쉬타이너 망이다.

이제 위의 조건들이 '최소길이'를 갖는다는 것을 하나하나 밝혀보기로 하자.

기초정리 1 : 선분들로 이루어져 있다.

기초정리 2 : 하나의 꼭지점에서 뻗어나간 어떤 두 선분이 이루는 각은 120도 보다 작지 않다.

따라서 하나의 꼭지점에서는 세 개의 선분을 넘을 수는 없다. 그렇게 되면 120도를 넘게 될테니까.

기초정리 3 : 두개의 선분이 뻗어 나올 경우 이들이 이루는 각은 120도 보다 크거나 같다. 만약 세 개의 선분이 뻗어 나올 경우 이것들 사이의 각은 120도다.

쉬타이너 망을 어떻게 짤까?

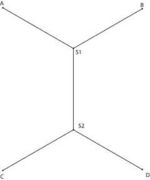
만약 k 개의 점이 있다고 한다면 쉬타이너 망이 그 점을 최소의 길이로 잇는 도형이라는 것은 앞에서 밝혔다. 이로써 네 마을의 촌장들은 물자를 아껴서 길을 낼 수 있게 되었다. 그 모양은 옆의 그림처럼 될 것이다.

자, 여기서 멈추지 말고 생각을 더 해보자. 세월이 흘러 마을들은 더 분화해가면서 발전해갔다고 상상해보자. 이제가 마을이 넷이 아니라 k 개가 되었다. 다시 길을 놓아야 할 시점에 이르렀다. k 개의 마을에서 k 명의 촌장들이 다시 모여 회의를 열었다. 역시 하나의 마을도 고립되지 않도록 길을 만들되 최소 길이로 하자고 의견을 모았다. 우리에게는 쉬타이너 해법이 있기 때문에 '바로 그렇게' 만들면 된다는 것을 알 수 있다. 그러나 '과연 어떻게?' , 어떻게 그 망을 설계할 수 있을까? 해법이 하나만 있을까? k 개의 마을을 잇는 최적으로 방법은 몇 개가 가능할까?

MaxMin 문제 - 들아가는 말 로 돌아가기

Note

↑ 따라서 하나의 꼭지점에서는 세 개의 선분을 넘을 수는 없다. 그렇게 되면 120도를 넘게 될테니까.

[1] 따라서 하나의 꼭지점에서는 세 개의 선분을 넘을 수는 없다. 그렇게 되면 120도를 넘게 될테니까.

[1]