Math is SinHwa
수학은 신화다
수학은 신화다. 신화는 수학이 될 수 없으나, 수학은 신화다. 따라서 수학만 신화인 것은 아니다. 이것이 오늘 나의 수학 언어에 대한 깨달음이다. 수학은 왜 신화인가 ?
神話는 신들의 이야기다.
신들에 대한 이야기이고 신들의 이야기다. 결국, 신들의 이야기는 신의 이야기이다. 그 역도 성립한다. 신들은 신이며 신은 신들이다. 그것이 개체가 아닌 총체로서의 신이다.
신은 무슨 이야기를 주고 받았던가? 신들에 대해 우리는 무엇을 이야기했던가 ? 삶에 대해 이야기했다. 살아 있는 동안 일어나는 모든 일에 대하여 죽음에 대하여 죽음 이후에 대하여, 삶 이전에 대하여. '대하여' 이야기하였다.
신은 추상적 존재다. 추상의 형상화다. 삶의 몸과 마음들을 용광로에 넣었다가 다시 탄생시켰다. 왜? 신이 그렇게 시켰다. 신은 나다. 내 안에 신이 있다. 신 속에 내가 있다. 삼천년 전 동굴 속에 짱돌로 벽에 그림을 그리던 이, 신을 탄생시켰다. 왜? 신이 그렇게 시켰다. 먹이감 부족해서 그랬다. 먹이감이 남아돌아서 그랬다. 배고파서 그렸고 배불러서 그렸다. 그리고 언어를 탄생시켰다. 그림은 현실의 대응물이지만, 현실을 대체할 수는 없었다. 말이 필요했다. 그래서 말을 했다. 말은 점점 정교하게 만들었다. 누가? 내가. 신이 그렇게 시켰다. 말은 점점 이야기를 만들어냈다. 함부로 말할 수 없기도 했다. 함부로 말한들 다 말할 수 없기도 했다. '바로 그것'을 말은 표현하지 못했다. 그래서 이야기를 만들었다. 이야기의 주인공은 모두 나였다. 동굴 속에 그림을 그리던 손은 석굴암의 본존불상을 정으로 쪼았다.
신은 자신을 만들라고 말했다. 신이 말하지 않았으면 신을 만들지 않았을 것이다. 땅과 하늘, 산과 바다, 들과 강, 나무와 풀, 작은 새와 사나운 짐승, 기름진 땅과 눈서리... 이것들은 서로 다른 신을 만들었다. 하지만 신은 점점 추상화된다. 추상화되면 더 모호해지지만 더 강력해진다. 모호하게 말할수록 속내가 더 깊어 보였다. 신은 몸뚱도 필요로 했다. 그래서 나를 만들어라 하였다. 그래서? 만들었다. 하얀 피부를 가진 사람들은 신을 하얗게 만들고 까만 피부를 가진 사람들은 신을 까맣게 만들었다.
신은 그렇게 구체적일 수 없다. 그렇다면 삶의 이야기를 풀어 말할 수 없다. 구체적일수록 날카롭다. 직선은 면적을 갖지 않는다. 하지만 모든 직선은 평면에서 논다. 공간이 바뀌면 법칙도 바뀐다.
신은 추상화되어 있을 때 신이다. 모호하게 말할 때 신이다. 신의 궁극적 형상은 원이나 직선으로 표현된다. 그것들의 조합으로 드러나기도 하지만, 조합되서 더 구체적이 되어가면서 신은 신으로부터 멀어져 인간의 형상을 하게 된다. 무당들은 구체적인 신을 모시는 사람들이다. 현대적일 수 없다. 현대인의 삶은 조각났다. 구체적인 신이 만족시킬 수 없다.
수학은 神話다.
내 앞에는 동전과, 엽서가 있다. 엽서는 직각사각형 모양이고, 동전은 원의 모양이다. 천장에서 전등을 달은 전선은 직선 모양으로 내려 앉았다. 호랑이를 그린 그림은 형체를 알기 어렵다. 수많은 도형들이 버무려져 있다. 색과 선으로 그 안에 담긴 추상성을 가리고 있다.
수, 도형, 함수, 집합, 벡터 같은 것들은 추상적이다. 구체적이지 못하다. 이것들은 어디에도 없지만 어디에나 있다. 파도의 포말에도 산에서 불어 내려오는 가을 바람에도 있다. 떨어지는 낙엽에도 있고 장마 장대비에도 있다. 한 해 처음으로 피어난 꽃망울에도 있다.
직선과 직선이 만난다. 어떤 수가 다른 수를 더해 또 다른 수를 낸다. 집합과 집합은 대응한다. 대응하는 규칙이 드러난다. 그래서? 왜? 그럴 수 밖에 없었다. 술을 마시고 흥이 나면 노래를 부르고 춤을 출 수 밖에 없는 것과 같다.
다시, 직선과 직선이 만난다. 직선은 연속적이다. 직선이 한점에서 꺽이면 각을 이룬다. 다시 꺽여 닫히면 폐곡선을 만든다. 이것을 삼각형이라고 한다. 물론 삼각형은 세 점이 주어지고 그것을 이을 때도 가능하다. 서로 다른 탄생 배경을 갖지만, 삼각형은 삼각형이다. 삼각형이 원을 닮기 위해서는 자신의 '직선성'을 당장 포기해야 한다. 또는? 또는 한번 더 꺽어주어야 한다. 꺽임이 많아질수록 원을 닮을 수 있다. 하지만 어떤 다각형도 원과 같을 수 없다. 직선성의 경계를 넘어서는 다각형은 없다. 하지만, 천 번 만 번 꺽으면 사람들은 그것을 원이라 인식힌다. 그것이 사람이다. 사람의 시각은 연속적이지 않다. 꿈에서 깨어날 때 처럼, 살다가 죽을 때 처럼, 죽었다가 살아날 때 처럼, 시작과 끝을 가진다. 연속적이지 않다.
변들의 길이가 다르면 다른 삼각형이라고 인식하는 것이 사람이다. 잘못된 것 없다. 다르다. 길이는 분명히 다르다. 하지만, 그것의 성질은? 길이를 빼고 길이에 종속적이지 않은 성질들은? 삼각형끼리 같을 수 있다. 관점이 길이에 있는 한 삼각형은 달라보인다. 관점이 직선의 만남들이라고 생각하면, 직선이 두번꺽여서 닫힌 도형이라고 생각하면 그것만을 필요로하는 성질은 변함이 없다. 이런 세상에서는 다른 삼각형이 다르지 않다. 구체적인 신들의 세상이다.
아... 이게 아닌데...
예
점들의 무리와 한 점
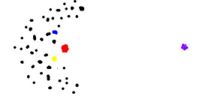

점의 무리들이 우두두두 모여 있다고 하자. 이 점들이 거기 있기 때문에 가질 수 밖에 없는 운명.[1]
빨간 점은 바로 거기, 점들의 무리에 있었던 빨간 점은, 파란 점에게 가까이 가려하면 할 수록 노란 점으로 멀어지게 된다. 무 리 안의 어떤 점도 마찬가지다. 대신 멀리 떨어진 보라새 점은, 한꺼번에 점들에게 가까이갈 수 있다. (토폴로지 증명) 이 점은 무한히 떨어져 있을 수록 더 그렇다. 하지만 보라색 점도 정에 이끌려 가까이 오기를 가까이 오기를 하다가는... 점들의 무리를 하나만 그렸지만 무리들도 여럿일 수 있다.
자, 이제 '가까이가다'를 인간의 어떤 감정, 관계라 한다면 ?
Bernard Show의 어떤 희곡(?). 남주인공이 여주인공에게 묻는다.
- - 그렇게 제멋대로인 사람들을 어떻게 그렇게 잘 다스릴 수 있는지
- - (생각에 잠겼다가) 그건 내가 본질적으로 모든 사람들으로부터 멀리 떨어져 있기 때문이라고 해명할 수 있겠어요.
벌떼의 움직임
벌 떼를 가까이서 보면 우르르 제멋대로 나는 것 처럼 보이지만, 멀리서 보면 그 무리는 분명한 목적을 가지고 정해놓은 방향으로 가고 있다. [2]. 소수의 움직임은 자연수를 따라 정해진 규칙대로 움직이지 않는다. '거의' 그럴 듯한, 근사한, 규칙은 나오지만, 소수의 법칙성은 발견되지 않는다. 가우스의 발견 이후 지금까지 이 '근사적 규칙'은 점점 더 발전했지만, 여태 개별적인 벌들의 움직임들 까지 모두 파악해내지는 못했다.
- 소수의 분포 참고.
소수의 규칙에 대한 연구는 그 규칙없는 규칙에 대한 연구일 수 있다. 무질서의 질서가 갖는 아름다움으로의 동경 같은...
Note
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia