Construction-box

음악에서 모짜르트, 문학에서 세익스피어, 미술에서 미켈란젤로와 어깨를 나란히 하는 수학계의 거장이 가우스다. 그는 말보다 셈을 먼저 배웠다고 할만큼 신동이었다. 전해오는 말로만 따져 보았을 때 꼬마 가우스가 남긴 전설같은 재능에 견줄 수 있는 사람은 드물다. 가우스를 매우 유명하게 만든 일화들이 여러 개 전하지만 그 중 가장 유명한 일화는 1 부터 100까지의 덧셈이다. 그가 초등학교에 입학한 것은 만 7세때다. 처음 두 해는 덧셈 뺄셈을 배웠기 때문에 가우스가 특별하게 두드러질 계기는 없었다. 가우스의 신동은 3 학년때 드러났다. 한꺼번에 여러 학년을 가르쳐야했던 뷰터너 선생님은 종종 풀이가 오래 걸리는 문제를 칠판에 적고 학생들이 풀게 했다. 그날은 1 + 2 + 3 + ... + 100 을 적었다. 그동안 다른 학년을 지도하려고 했던 것이다. 그런데 선생님이 칠판에 적자 마자 몇 초 지나 가우스가 5050 이라는 답을 적었다. 선생님이 1 + 2 + 3 + ... 를 적는 동안 번개처럼 어떤 생각이 스쳐지나갔고 평소에 셈이 매우 빨랐던 가우스는 마지막으로 100을 적자는 순간 답을 냈던 것이다. 오죽했으면 지금도 왠만한 책에서는 ‘가우스 덧셈’이라는 이름까지 붙인다. 그의 머리에 무엇이 스치고 지났을까?

닥친 문제의 형태를 바꾼다

그는 1과 2 를 더하고 그 결과에 3을 더하는 보통의 방법을 쓰지 않았다. 던져진 질문을 그대로 받아들이지 않은 것이다. 그는

1 + 2 + 3 + ... + 98 + 99 + 100

이라는 문제에 같은 수만큼을 더한 것이다. 대신 그대로 더한 것이 아니라 100 + 99 + 98 + ... + 3 + 2 + 1 로 해서 더한 것이다. 이제 1 과 100을 더하고, 2와 99를 더하고, 3과 98을 더해가는 절차를 계속해가서 마지막에 99에 2를 더하고, 100 에 1을 더하게 된다. 그렇다면 101이 100개 된다. 이것은 구하고자 하는 값을 두 배해서 만들어낸 것이기 때문에 그만큼 덜어내면 된다. 101 이 100개 있는데서 반인 50개를 덜어내면, 결국 101 이 50개가 된다. 101 곱하기 50은 계산에서 탁월한 재능을 보인 가우스에게 식은죽 먹기 였다. 하지만, 실제로 가우스가 그 방법을 적용해서 덧셈을 했다면 그것은 실제로 놀라운 발견이 아닐 수 없다. 왜냐하면 칠판에 써진 문제는

1 + 2 + 3 + ... + 100

이었으니 눈에 보이는 것만 가지고 풀어가는 것이 보통일텐데, 이 방법은 눈에 보이지않는 것을 잠시 가져와 더한 다음 나중에 다시 덜어내는 방법을 쓴 것이다. 풀이를 보고 나면 싱겁다고 생각할지 모르지만, 10살 소년이 이런 생각을 한다는 것은 놀라운 일이다. 지금도 이렇게 일정한 만큼 더해져가는 수들을 등차수열이라고 한다. 풀이 아래 깔린 기막힌 착상은 꼭 이 덧셈에만 쓰이는 것이 아니다.

같은 만큼 더해주고 나중에 뺀다

같은 만큼 더해주고 빼면 된다는 생각은 수학 뿐만 아니라 일상에서도 자주 일어난다. 예를들어 책들이 빼곡하게 채워진 책장에 책 한 권을 더 꼽으려면, 이미 채워진 책장에서 두어권을 반 쯤 빼내고 그 사이에 끼우려고 하는 책을 사이에 넣은 다음세 권을 한꺼번에 밀어 넣으면 쉽게 들어간다. 해결해야할 문제가 있으면 그 문제를 있는 그대로 놓고 풀려고 하면 안풀릴 때, 그 문제를 조작해서 형태를 바꾸어볼 필요가 있다. 가우스가 소년 때 스스로 터득했던 이런 생각은 수학의 쉴 새 없이 등장한다.

삼각형의 넓이를 구해보자. 삼각형의 넓이를 나타내는 공식을 적용할 사람들이 있겠지만, 주어진공식을 외워 쓰는 것은 그것만 알게 될 뿐이다. 물고기만 얻는 게 아니라 고기 잡는 법을 배운다는 것은 스스로 문제를 해결하려는 사람에게만 주어지는 선물이다. 삼각형의 넓이를 구해 보해보자. 왼쪽 그림처럼 처음에 있는 파란 삼각형의 넓이를 구한다고 하자. 다르게 구할 수 있는 방법도 있지만 같은 모양의 가상의 빨간 삼각형을 있다고 가정해서 그것을 원래 있던 것에 포개면 된다. 이제 문제는 직사각형 넓이 구하는 것이 되었다. 우리는 직사각형의 넓이만 구하면 문제를 해결할 수 있다. 알다시피 직사각형의 넓이는 밑변 곱하기 높이다. 이렇게 나온 것에서 반만 뽑아내면 삼각형의 넓이가 되는 것이다.

기본 생각을 확장한다

이 착상을 다른 곳에서 자유롭게 응용해볼 수 있다. 원의 넓이를 구해 보자. 아래 그림처럼 원판을 12조각으로 똑같이 잘라서 오른쪽 처럼 놓는다. 그렇게 되면 12 개의 송곳이빨 같은 모양들이 줄줄이 설 것이다. 여기에 똑같은 반대쪽에서 끼워넣으면 넓이는 두배가 될 것이다. 그렇다면 위쪽에 튀어 나와있는 동그란 조각들 12 개의 길이는 원의 둘레와 같아질 것이고 옆의 선분의 길이는 원의 반지름과 같다.

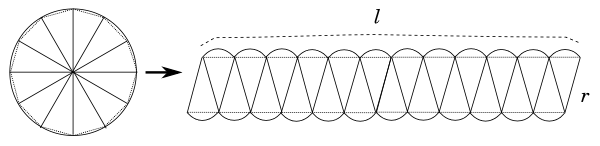
아직은 이것으로 원의 넓이를 구할 수 어렵다. 그런데 12 조각이 아니라, 24 조각, 48조각, 96 조각으로 계속 쪼개면서 이 생각을 발전해간다고 하자. 이 과정을 해갈수록 윗니와 아랫니를 붙인 조각은 긴 쪽 길이는 원의 둘레인 l 이고 짧은 쪽 길이는 반지름 r 인 직사각형의 넓이와 구별하기 어려울 만큼 아주 비슷해질 것이다. 그래서 원의 넓이는 원의 둘레 곱하기 반지름이 된다.

물음표에서 느낌표로, 느낌표에서 다시 물음표로

물론 상황은 여기서 종료되지 않는다. 원의 둘레를 어떻게 찾을까 하는 것이 문제다. 그보다 더 큰 문제가 있다. 아무리 잘게 쪼개도 눈으로 구별이 안될만큼 비슷하다고 해도 같을 수느 없지 않을까? 끝없이 많이 쪼개버리면 어떨까? 그렇다면 점점 비슷해져서 마침내 같아질 것 같긴 하다. 하지만 그렇게 호락호락하지 않게 해결될 문제가 아니다. 왜냐하면 끝없이 잘개 쪼개버리면 길이가 r 인 반지름이라는 선분들만 남기 때문이다. 선분은 넓이를 갖지 않은 순수한 선일 뿐이기 때문에 넓이는 0 이다. 0 을 무한히 많이 더해봤자 0 은 0일 뿐이다. 원판은 뚜렷하게 넓이를 갖는다. 어떻게 이 둘이 같아질 수 있단 말인가? 끝없이 더한다면 같아질 것이라는 우리의 소박한 직관을 함부로 믿을 수 없게 만드는 예는 얼마든지 들 수 있다. 그래서 여기까지 생각해두고 완전히 믿을만 하도록 엄격하게 이 체계를 다듬기 까지는 2 천 여년을 더 기다려야했다. 이 이야기를 계속할 수는 없다. 하지만, 하나의 물음표에서 느낌표를 얻었다고 해도 거기서 끝내지지 않고 다시 새로운 물음표를 불러 온다는 것은 앞에 던진 질문 둘 만으로도 알 수 있다. 사실은 원의 둘레 문제는 결국 둘째 질문과 다를 것이 없다.

어쨌든 여기서 중요한 것은 어린 가우스가 해낸 착상은 생각의 기초까지 깊이 끌고 내려가지 않으면 쉽지 않은 것이라는 점이다. 가우스의 천재성은 바로 그것을 한 순간에 어쩌면 그 자신도 의식하지 못한 채 번쩍 하는 사이에 그곳으로 순간이동한 것이라 볼수 있다. 그리고 우리는 이제 그의 순간이동을 분석해서 보게 된 것이다.

사실, 가우스가 실제로 실제로 1 부터 100을 더하는 문제를 그렇게 풀었는지는 분명하게 알 수 없다. 전하는 책마다 문제나 숫자가 다르기 때문이다. 하지만, 소년 가우스의 빼어난 재능이 조그만 마을이었던 브라운쉬베이그를 떠들썩하게 한 것은 분명하다. 이로부터 가난한 집안에서 어렵게 공부하던 가우스의 재능은 멀리까지 퍼져나가 곧 평생 후견인이 될 페르난데스 공작의 귀에까지 들어가게 되었다. 이로써 재정적으로 안정되었을 던 것만은 아니다. 그의 재능을 알아본 선배이자 수학에 흥미를 많이 갖고 독학으로 수학 공부를 열심히 하고 있던 바르텔스라는 사람을 만나 함께 공부하게 된다. 바르텔스는 이미 수학 공부의 자료가 꽤 있었던 덕분에 소년 가우스는 귀중한 수학 정보와 맞닿게 된다. 바르텔스라는 사람의 수학적 업적은 별로 알려지지 않았지만, 그는 수학의 역사에서 매우 흥미로운 사람이다. 그는 가우스의 선배로 함께 공부를 했고, 나중에 러시아의 까잔 대학 교수로 갔을 때는 로바체프스키라는 수학의 역사에 한 획을 그은 또 하나의 천재를 가르치게 된다.