Max in polygon

Max 문제 증명의 논리적 결함

기초 문제

아래의 문제들은 보기에 매우 쉬어서 어떤 이들은 '반짝이는' 머리로 금방 해답을 찾을 수 있을지 모른다. 그렇지만, 그것이 정말 왜 그런지 보이는 과정을 밟지 않는다면 '더 복잡한' 문제를 푸는데 어려움이 있게 될 것이다. 풀기 전에 먼저 생각해보라.

삼각형 모양의 면이 있다고 하자. 그 면에서 가장 긴 길이를 갖는 두 점은 ?

이제 어떤 n 각형으로 일반화 시켜 확장해보자. 게다가 이 n 각형은 볼록이 아니어도 된다. 그런 n 각형안에 어떻게 두 점을 잡아야 Max 길이를 갖게 될까?

어떤 n 각형으로 된 평면이 주어지든 Max 길이를 갖는 두 점은 ?

기초 문제 : 삼각면의 Max 길이 갖는 두 점

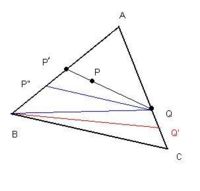
삼각형 모양의 면이 있다고 하자. 그 면에서 가장 긴 길이를 갖는 두 점은 ? 물론 가장 긴 변의 두 꼭지점일것이라 짐작하는 것은 어렵지 않아 보인다. 하지만 정말 그럴까?

아무 점이나 두 점 P, Q 을 잡는다. 두 점 중 하나라도 변에 있지 않으면 변까지 연장할 수 있다.
변 위에 점을 잡는다. 서로 다른 변에 있다고 해보자. 두 점 중 하나를 꼭지점까지 연장할 수 있다. (P' $\rightarrow$ P $\rightarrow$ B )
나머지 하나도 꼭지점까지 연장할 수 있다. 따라서 가장 긴 두 변을 이루는 꼭지점 두 개가 우리가 찾는 두 점이다. (Q $\rightarrow$ Q' $\rightarrow$ C)

정말 그렇다. :)

그렇다면 위에서 일반화된 문제의 답은 ? 그렇다. 두 꼭지점을 잇는 선분 중 가장 긴 선을 고르면 된다. (구체적으로 어떻게 증명할 것인가?)

기초 문제 : Max 면적을 갖는 삼각형이 되는 원 위의 세 점

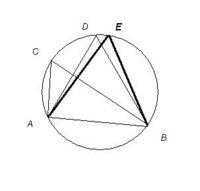
원이 있다. 그 안에 세 점을 골라 삼각형을 이룰 때, 그 삼각형이 Max 면적을 갖도록 세 점을 잡는다면 어떤 것을 잡아야 할까?

원에서 아무거나 세 점 A, B, C 을 고른다. 한 변(AB)을 고정하고 두 변(AC, BC)을 살핀다. 두 길이가 다르다면, 두 변의 길이가 갖도록 점을 옮길 수 있다. 그럴 때 높이가 커지므로 면적은 커진다. (C $\rightarrow$ D )
두 변의 길이가 같을 때 까지 (E) 옮긴다.
이제 두 변을 같게 했으니 그 중 한 변과 처음 고정한 변과 비교한다. 마찬가지로 두 변의 길이가 같도록 옮길 때 높이가 커져 면적은 커진다.
그래서 세 점은 정삼각형을 이루는 세 점이어야 한다.

증명에 대하여

위의 증명은 모두 다음과 같은 방식을 따르고 있다. 주어진 조건이 있고, 그 조건에서 max 조건을 만족하도록 점들을 골랐다. 그것을 증명하는 방법은 아래와 같았다.

아무거나 (두 점이건, 세점이건) 잡는다.
예를들어 두 점이라면, 어떤 한 점에 대해 골라낸 다른 점의 '곁' 에 max 가 되게하는 점을 찾는다.
그런 과정을 되풀이 하면서 문제에서 요구하는 최적점을 찾는다.

이런 방법은 흔한 방법인데, 치명적인 논리적 결함이 있다는 것이 19세기에야 드러났다. (Beierstrass) 먼저 예를 하나들어보자.

n 각형 평면에 대한 정리의 논리적 증명

앞에서 어떤 n 각형에 대해서도 적용된다던 증명 방법은 분명히 논리적 결함이 있었다. 이것을 어떻게 극복할 수 있을까?

n-다각형 이 주어졌다고 하자. 아무 점이나 두 점 P, Q 을 찍는다.
선분 PQ 에 수직인 두 직선 l, m 을 긋는다. l 이 '왼쪽' , m 이 '오른쪽' 직선이라고 하자.
l 은 한 꼭지점을 지나거나 그 '왼쪽' 에 한 꼭지점 A 이 있을 것이고, m 도 한꼭지점을 지나거나 그 '오른쪽'에 다른 꼭지점 B 이 있을 것이다.
그렇다면 선분 PQ 는 항상 두 꼭지점 AB 보다 짧다. 다시 말해 꼭지점을 잇는 선분은 '임의의 어떤 두 점' 보다 길다.
따라서 '꼭지점'을 잇는 두 선분의 길이가 항상 더 길다.

이 증명에서 쓰인 단순한 사실들을 확인하고 이 증명이 앞의 증명과 무엇이 다른지 보도록 하자. 앞에서 쓰인 평행한 두 직선 위의 가장 짧은 두 점은 두 평행한 직선에 수직이 되는 두 점이다. 다시 말해,

평행한 두 직선이 있다고 하자.(l, m) 그 직선들과 수직인 직선이 만나는 두 점을 잇는 선분은 두 직선에 속한 어떤 두 점을 잇는 것보다 같거나 짧을 것이다. 평행한 두 직선 '사이'에 있지 않고 '바깥쪽' 에 있는 두 점에 대해서는 더 말할 나위 없다.

\forall Q(\forall P\exists P'\ (QP<QP')

의 논리에 이 과정을 '계속' 반복해 가면서 '더 최적의 값'을 찾아갈 수 있다는 논리였다. 따라서 앞에서 지적한 '특별한 경우'의 논리적 함정에 빠질 위험이 있었다.

그에 비해 바로 위의 증명은 앞의 경우 처럼 max 가 존재한다고 가정하고, 임의의 두 점을 찍은 다음, 그것보다 더 큰 값을 주는 다른 위치를 찾아가는 논리가 아니라는 점에 주목하라. 이 증명은 어떤 두 점에 대해서도 더 길거나 같은 꼭지점의 두 점이 존재할 수 밖에 없다는 것을 보인다.

\forall P,Q\exists A,B\ (PQ<AB)