Number Theory 1 2 3

Invitation to number theory

by Oystein Ore , Math associtation of America , 20

Ch.1 : Introduction

역사

자연수 1, 2, 3, ... 과 같은 수들을 양의 정수라고 부르는데 이런 수들은 '세는 행위(to count)'와 함께 발달해왔다. 처음엔 덧셈을 주로 했고, 세월이 많이 흘러 곱셈과 뺄셈을 하게 되고 나눗셈도 그 뒤를 따르게 되었다. 이런 연산(operation)을 calculation 이라고 부르는데 그 어원은 calculus 라는 라틴어에서 왔고, 다시, 그 말은 계산할 때 쓰던 '조약돌' 을 뜻한다.

오랜 역사과정에서 계산의 경험이 축적되면서 수 안에 담긴 특성들을 발견하고 더 깊은 탐구해들어 가게 된다. 현대에 들어 자연수(정수)의 세계를 탐구하는 이런 분야를 '수론(number theory)'이라 한다.

= 수에 대한 믿음

'수'는 오래 전부터 어떤 묘한 느낌이나 믿음을 가지기도 했다. 예를들어 고대 그리스에서는 2 를 여성, 3 을 남성이라고 보았고, 5를 그것의 통합, 결혼을 뜻하는 상징이라고 보기도 했다. 이에 대해서는 플라톤의 저술 Republic (국가, 공화국) 8권을 보면 이런 식의 수에 대한 믿음들에 대해 더 많은 것을 알 수 있다. 고대 그리스에서만 이런 것이 아니고, 기독교 문화도 독특한 수에 대한 믿음을 갖기도 한다. 13 이라는 숫자는 '최후의 만찬' 에서 13번째 손님으로 온 유다를 상징하여 좋지 않은 느낌을 주눈 수라, 서양에서는 13 층이나 13 번 방이 없곤 한다. 또 구약에서는 7 이 특별한 숫자다. 문화마다 다른 증거들도 있는데, 고대 독일 이야기들에서는 3 과 9 가 특별한 지위를 갖고, 힌두 문화에서는 10 이 매우 특별한 역할을 하기도 한다.

= 피타고라스 수

피타고라스 수는 피타고라스 정리가 성립하는 자연수의 쌍을 말한다. 예를들면 (3,4,5) , (5,12,13) , (8, 15, 17) , ... 같은 수들의 쌍이다. 이 수들은 나일강이 범람하여 새로 농지를 재야 할 때, 건축을 할때, 모두 '직각'을 잴 때 매우 중요한 역할을 하였다. 이런 수들의 성질에 대해 본격으로 연구한 저술은 기원후 200여년 경의 알렉산드리아의 디오판테스가 남긴 것으로 알려진 'Arithmetica' 일 것이다. 그 때 이후로 어떤 등식에서 정수나 유리수 해를 찾는 것을 디오판테스 문제라고 하며 이는 오늘날 수론에서 중요한 분야이다.

다각수

고대 그리스에서는 수를 기하적 도형과 연결지어서 생각하였다. 그래서 9 같은 수는 3의 제곱으로, 100 은 10의 제곱으로 정사각형과 연결지어 생각했고, 27 은 3 의 세제곱, 125는 5의 세제곱 처럼 큐빅과 연결지어 생각했다. 또 20 이란 수는 4 곱하기 5 로 나타낼 수 있어서 이렇게 어떤 두 수의 곱으로 표현할 수 있는 수를 사각형 수라고 불렀다. 이런 수들은 두 수의 곱을 모두 한 변과 다른 변으로 해서 나타낼 수 있다. 다만, 5 와 같은 수는 그렇게 나타내려면 한 변이 오로지 1 일때만 가능했다. 이런 수들을 모두 모아 'prime' 이라고 말했고 지금도 그렇게 부른다. prime number 다만, 이 때, 점이 하나 만 있는 경우는 워낙 기초적인 것이라 수를 이루는 기초 중의 기초라고 보아서 prime 이라고 보지 않았다.

다각수에서 유명한 것들 몇 개만 보자.

• 삼각수 : 1, 3, 6, 10 으로 가는 수들이다. 이런 수에 해당하는 점의 갯수로 삼각형 꼴을 만들 수 있다. 이것은 재미있는 성질을 갖는다.
  • 연속하는 두 삼각수는 어떤 수의 제곱수다. 1+ 3 = 4, 3+ 6 = 9
  • n 번째까지 전개한 삼각형 수의 점의 총갯수는 ${\frac {n(n+1)}{2}}$ 다.
• 4 각형 수 : 1, 3, 5, 7 , 9, ... 같은 수들이다. 이 수들도 흥미로운 성질을 갖는다.
  • n 번째까지 전개한 사각형 수의 점의 총갯수는 $n^{2}$ 이다.
• 5 각형 수 : 1, 5, 12, 22, 35 같은 수들이다. n 번째까지 전개한 오각수의 점의 총합은 ${\frac {n(3n-1)}{2}}$ 다.
• 일반적으로 k 각형 수를 n 번째까지 전개하면 점들의 총갯수는 : ${\frac {(k-2)n^{2}-(k-4)n}{2}}$ 다.

Magic Squares

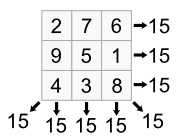
n 곱하기 n 개의 정사각형 틀에 수를 넣되, 모든 행의 합이 같고, 열도 같고, 대각선도 같도록 수를 채우면 그것을 magic square 라고 한다. 오른쪽에 있는 3 곱하기 3의 경우는 그것을 만들 수 있는 경우가 유일하다.