Conic Section MaxMin

Conic Section에 대해서는 Conic Section의 정의 부분을 참고하세요. (지금은 조금, 앞으로 추가 됩니다. :) )

Heron 정리는 문장이 단순명료하고 증명이 명쾌하다. 주어진 직선으로 나뉘는 평면의 한 쪽에 놓인 두 점을 '최소거리'로 잇는다는 수학적 사실은 여러 형태로 '해석'해 볼 수 있다. 그 중 처음 Heron 연구의 동기였다고 할만한 '거울에 반사하는 빛의 운동'으로 해석해 볼 경우, Conic Section의 촛점과 접선들의 관계가 설명하는 기초적인 광학적 성질을 알아낼 수 있다. 여기서는 거울이 휘어 있는 경우 중 타원형, 쌍곡선 형, 타원형으로 휜, 특수한 어떤 경우들을 보는 셈이다. 빛과 반사를 포함해서 광학적으로 어떻게 응용될 수 있는지 보자.

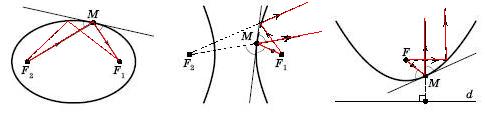
Conic Section위의 한 점과 촛점의 거리

Conic Section이 타원, 쌍곡선, 포물선의 형을 가진다는 사실은 Conic Section의 정의 에서 말한 바 그대로 다음과 같이 정의될 수도 있다.

• 타원 := 주어진 두 점 $F_{1},F_{2}$ 에서 거리의 합이 같은 점들의 집합
• 쌍곡선 := 주어진 두 점 $F_{1},F_{2}$ 에서 거리가 차가 같은 점들의 집합
• 포물선  := 주어진 직선과 주어진 점 F로 부터 거리가 같은 점들의 집합

따라서 Heron의 정리로부터 다음과 같은 성질을 유추할 수 있다.

• 타원의 한 점 M의 접선과 두 촛점을 잇는 선분과 M이 이루는 두 각은 접선에 대해 같다.
• 쌍곡선의 한 점 M의 접선과 두 촛점을 잇는 선분과 M이 이루는 각을 이 이루는 각은 같다.
• 포물선의 축과 '직선' MF가 이루는 각은 같다. 여기서 축은 포물선을 정의했던 직선과 직각인 직선이다.

위의 사실들은 어떻게 증명할까? 아래 증명을 참고하라.

증명 Sketch

타원에 대해서 보도록 하자.

• 주어진 두 점 $F_{1},F_{2}$ 와 주어진 직선 L 이 이루는 최단 거리를 c 라 하자. 그리고 선분의 길이 $F_{1}M$ 를 a, $F_{2}M$ 를 b 라 하자.
• a + b 가 c 가 되는 점들의 집합은 타원을 이룬다.
• 만약 L이 타원에 걸쳐 있거나 L이 타원의 밖에 있으면 최단 거리의 가정으로부터 모순이 생긴다.
• 그래서 L은 타원과 접선이다.
• 따라서 Heron의 정리에 따라 두 촛점을 잇는 선분과 M이 이루는 두 각은 접선에 대해 같다.

쌍곡선에 대해서는 변형된 Heron 정리로부터 유도된다. 이 때의 변형은 주어진 직선이 나누는 반평면에 한 점씩 주어졌을 때 두 점이 이루는 거리 차의 절대값이 최대가 되는 점의 작도와 관련하여 풀 수 있다. (WIM 8-1-4 참조)

광학적 성질과 응용

이로부터 다음의 광학적 사실들을 발견할 수 있다. conic section들이 모두 이상적인 거울로 되어 있다고 상상해보자.

• 타원의 한 촛점에서 타원에 빛줄기들을 쏘면 그 빛은 반드시 다른 촛점을 지난다.
• 쌍곡선의 한 촛점에서 빛줄기들을 쏘면 빛은 발산한다. 이 발산하는 빛줄기들을 그 반대쪽으로 연장하면 다른 촛점에서 모두 만난다.
• 포물선이 촛점으로부터 나오는 빛들은 모두 평행하게 뻗어나간다.

위에서 본 성질을 응용하여 다음과 같은 기구를 만들어낼 수 있다.

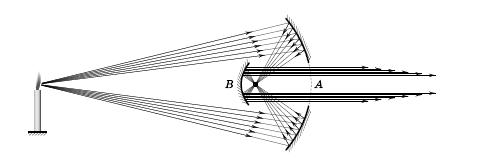
• 포물선형 거울과 전구의 위치를 촛점에 둘 경우 나오는 빛은 평행하게 직선으로 뻗어나갈 수 있다.
• 쌍곡선 형의 거울과 전구의 위치를 적당한 촛점에 둘 경우 나오는 빛은 넓게 퍼져나가게 할 수 있다.
• 타원형의 한 촛점에서 빛을 발산하면 빛들은 모두 다른 촛점에 모인다.
• 타원형과 포물선형을 중복해서 설계해보자. 타원의 한 촛점 A 에 빛의 발산지점을, 다른 촛점이 되는 지점 근처에 포물선 모양의 집적-반사판을 대보자. 포물선의 빛이 평행하게 나가는 쪽에는 타원을 뚫어놓는다. A 지점에서 빛을 발산하면 그 모든 빛들은 모두 타원의 촛점을 지나 포물선 집적판에 모여 반사하여 평행하게 뻗어나갈 것이다.

물론 위의 응용은 망원경을 만들 때 반사경과 렌즈, 송신장치와 수신장치 안테나를 만들 때도 응용된다.

단일폐곡선으로 일반화

Heron의 정리를 일반화할 때 우리는 직선이 주어졌다는 가정을 일반화해서 일반적인 곡선으로 바꾸어 볼 수 있다는 것을 언급했다. 대수적으로 일반화하여 미분개념을 도입하여 풀 수도 있지만 그 문제는 다른 주제로 달리 다루기로 하고 여기서는 단일 폐곡선에 대해서 기하학적인 해법이 가능한 경우를 본다.

먼저 다음 문제를 보자. 단일폐곡선은 주어진 평면을 둘로 쪼갠다.

어떤 점 A가 주어졌을 때 그 점과 이어 최소 길이와 최대 길이가 되는 단일 폐곡선의 점은 어떤 점일까?

문제를 Heron 문제와 같이 다음과 같이 바꾸어보자.

어떤 두 점 A, B 가 단일 폐곡선이 쪼개는 반평면의 한쪽에 있을 때, 두 길이의 합이 최소값이 되는 단일 폐곡선의 점은 어떤 점일까?

위의 문제에서 단일폐곡선에 대해 길이의 합이 최소가 되는 점 M 의 접선에서 주어진 두 점 A, B와 M과 접선이 이루는 각은 같을까?

위의 문제에서 단일 폐곡선의 반평면에 하나씩 점이 있을 때 선분의 차 AM - BM가 최대값이 되거나, 최소값이 되는 점을 찾고 그 점에서의 접선과 두 점이 이루는 각의 성질에 대해 밝혀라.

위의 문제 중 두번째는 다음과 같이 증명할 수 있다.

• AM과 BM의 선분의 길이의 합이 최소라고 하자. 그렇다면 A와 B를 촛점으로 하고 그 최소가 되는 길이로 타원을 얻을 수 있다.
• M에서 타원과 단일 폐곡선은 접한다. 접선도 같다.
• 앞의 타원에서 이미 밝혔듯, 접선과 두 선분이 이루는 각은 같다.

Note

Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia