취학전 수학에 대해

취학 전 수학에 대한 초심자의 고찰[에 대해 초보자가 생각해야 할 것]

취학 전 수학은 언제부터 시작되는가?

여러분 모두 이런 장면은 여러 번 보았을 것이다. 엄마가 커튼 뒤에 숨었다가 웃으면서 눈을 빼꼼 내밀고 <<까꿍!>> 하곤 다시 숨어버린다. 그럼 아직 완전 어린[젓먹이인] 애기는 엄마가 나타날 때마다 고사리 같은 손바닥으로 손벽을 치며, 좋아서 어쩔 줄을 모른다[좋아서 까르르 웃는다]. 엄마와 애기 둘 다 너무 행복해한다. 그리고 당연히 자기들이 수학 공부를 하고 있다는 사실은 생각도 못한다.

내가 이런 말을 쓴 것은 독자를 놀래키려 하거나 귀가 쏠깃하는 역설{의 낚시대}로 독자를 낚으려는 것이 아니다. 진지하게 하는 얘기이다. 심리학자들의 글을 읽어보면, 만 1,5세 이전 연령의 아이 앞에 놓여진 지적능력을 요하는 기본 과제들은 객체의 항상성의 법칙을 알게 하기 위한 것들이다[으로 귀결된다]. 다시말해, 우리가 어떤 물체[것, 물건]을 보기를 중단했는데도, 그것이 사라지지 않고 있었던 그 자리에 남아 {존재해}있다는 것은 우리없이도 존재한다는 것이다. 엄마와 같은 그런 중요한 대상은, 그것이 커튼 뒤로 사라졌다해도, 어쨌든 여기 어딘가에 계속 존재해있다는 것이고, 곧 그 커튼 뒤로부터 나타난다는 것이다.

아이가 자라고, 세계에 대한 아이의 이해력도 함께 자란다.

아주 작은 소녀가 재미있는 놀이를 하며 논다; 소녀는 바닥에 이리저리 흩어져있는 퍼즐조각을 하나씩 골라서 아빠에게 건넨다. 그럴 때 마다 아주 당당하게 <<자!>>라고 소리친다. 아빠가 퍼즐조각을 받자 소녀는 깔깔 웃어댄다. 아이는 얼마전에 <<자>>라는 단어를 익혔고, 그 단어를 쓸 수 있을 때 마다 사용한다. 어쩌다가 손놀림이 아직 좋지않은 소녀의 손이 한꺼번에 두개의 퍼즐조각을 집었다. 순간적으로 소녀는 어떻게 행동해야 할지 생각해본다[이 상황에 어떻게 반응할지 머리를 굴린다]; –아아..알았다!- 그러고는 아빠에게 퍼즐조각을 건네며 소리친다:<<자-자 !>>. 이 상황을 뿌쉬낀의 말을 빌어 써보고 싶어진다 :

아이의 생각을 따라가보는 것이 가장 재미있는 학문이다.

만 2세쯤 되면 이미 아주 많은 것을 습득한 [익힌] 상태다. 생후 2년 몇 개월 된 남자아이가 아침에 아빠에게 묻는다:

- 아빠, 아빠, 자요?

-아니, 안자 –아빠가 눈을 부비며 대답한다. – 아빠, 부엌에서 차 마시고 있어.

아이는 깜짝 놀란다. 이건 이전에 배웠던 모든 것과 모순되는 것이기 때문이다. 어쨌든 아이는 혹시나 해서 부엌으로 달려가 확인해본다. 그러고는 부엌에서 당당하게 돌아온다.

-아니잖아..아빠 부엌에 없잖아! 아아,,아빠..아빠 여기있잖아!

다음 번에는 아이를 그런 방법으로 대하는 것이 통하지 않을 것이다. 아이가 혹시나 해서 부엌으로 달려가 확인해 본 그 때, 제스스로 알아내려고 한 그 순간을 눈여겨 보고싶다{눈여겨 보자???}. 우리 모두는 이것이 아주 중요한 아동의 특성이라는 것과 그것이 좀 더 오래 유지된다면 더 좋을텐데..라는 것을 직감적으로 안다.

일본어로 셈을 해보자

시간이 얼마 지나지 않아, 아이는 이미 확실히 의식적인 <<수학 교육>>을 받게된다. 사실상 이것은 보통 셈하는 것을 배우게 될 것을 의미한다. 셈하는 능력이 매우 중요하고 유익한 것이라는 데는 이견이 없다. 그런데, 우리 성인들에게 이 능력이 실제로 무엇을 의미하는지를 이해하는 것은 매우 어렵기도 하다.

그럼 아이의 입장이 되어 우리가 직접 산수를 배워보자….그것도 일본어로! 자, 여기에 1부터 숫자 10개가 있다: 이찌, 니, 산, 시, 고, 로꾸, 시찌, 하찌, 큐우, 쥬우. 첫번째 과제는 이 숫자를 차례대로 외우는 것이다. 이게 그렇게 쉽지만은 않은 것을 여러분은 알게 될 것이다. 이것을 다 외우셨으면 두번째 과제로 넘어갈 수 있다; 쥬우부터 이짜까지 거꾸로 숫자 읽는 것을 익히시라. 이것도 다 된다면, 계산을 해보도록 하자. 로꾸에 산을 더하면 얼마인가?

P.10

그럼 시찌에서 고를 빼면? 그럼, 하찌에서 시를 나누면? 그렇다면 이제 문제를 풀어보자. 엄마가 시장에서 사과 꾸우 개를 사서 시 명의 아이들에게 사과 니 개씩을 나누어 주었다. 엄마에게 사과는 몇 개가 남았나? 매우 어렵긴 하지만, 반드시 지켜야 할 조건은 머리 속에서라도 러시아어{한국어}로 옮기지 않는 것이다. 이렇게 훈련하고 얼마 지나지 않아 그런 전환은 우리 뇌에서 우리의 의지에 반해 자동적으로 일어나게 된다. 아니면 아예 우리 스스로 전혀 깨닫지도 못할 것이다.

아이들이 저학년 과정에서 수행하는 그런 지적인 업적을 나는 나중에, 프랑스에 있으면서 제대로 평가하게 되었다. 이미 10년 이상을 여기서 살면서도, 아직도 나는 프랑스 숫자에 있어 문제를 겪곤 한다. 프랑스 인들은 70부터 99 사이의 숫자를 우리처럼 그렇게 셈하지[읽지] 않기 때문이다. 프랑스에서 육십 구 이후부터의 숫자는 육십-십(즉 70), 육십-십일(71), 육십-십이(72)...와 같이 이런 식으로 진행된다; 결국, 10단위(??) 끝에서는 육십-십구(79)가 된다; 이 이후에는 갑자기 사-이십(80), 사-이십-일(81), 사-이십-이(82),.....사-이십-구(89)가 되었다가, 다시 아까처럼 사-이십-십(90), 사-이십-십일(91), 사-이십-십이(92),...., 사-이십-십구(99)로 읽는다; 이 다음에는 드디어 백. 사람들이 내게 전화번호나 어떤 유명인의 생년월일 혹은 사망년월일을 아주 빨리 얘기하면 필요한 숫자를 항상 다 알아들을 수 있는 것은 아니다. {그나마} 나에게 이 숫자들을 다 더해서 계산해보라고 한 경우는 없어서 다행이다.

(안그래도, 이런 것에서 교육학책[교육론 교재]에서 자주 언급되는 프랑스 저학년생의 재미있는 대답이 나온다: <<이십에 사를 곱하면 얼마가 되지?>>라는 질문에 <<사-이십이 되지요, 곱하기는 교환이 되잖아요[곱하기에는 교환법칙이 있잖아요]>>

어쨌든 여러분은 결국 쥬우까지 빨리 셈하기를 다 익히셨으리라. 이것을 익히는데 시간이 얼마나 걸렸는가? 일주일? 한달? 이제 여러분은 여기에서 문제가 기계적인 기억{력}에만 있는 것이 아님을 깨달으셨을 것이다: 만약 그것만이 문제였다면 이 모든 일이 30분이면 다 끝났을 것이다. 그럼 기억력만의 문제가 아니라면, 무엇이 문제인가? 여러분은 여러분의 경험에서, 가지고 있는[던] 순수하게 수학적인 어려움들을 끄집어 낼 수 있겠는가? 셈의 영역에 있으나 우리 실생활 어디에선가 보이지도 않고, 미쳐 느끼지도 못하는 곳에 있는 그런 어려움들 말이다. 그게 그렇게 쉽지만은 않을 것이다, 그렇지 않은가?

어쩌면, 그러는 편이 더 나은지도 모르겠다. 그렇지 않으면, 초기 교육의 광신자들은 그 즉시, 아이가 아직 이해도 못하는 것을 아이에게 설명하느라 전력을 소모해 버렸을 것이다. 아이의 목덜미[옷깃]를 질질 끌어 좀 더 빨리 다음단계로 넣기를 바라면서.

사실 아이가 스스로 할 수도 있었을 것을...

유치원생을 위한 기하

그림 1. 왼쪽에는 정사각형이 그려져 있다. 그럼 오른쪽에는?

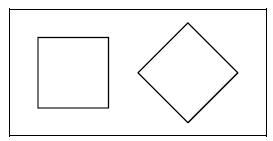
전통적으로 취학 전 수학에 나오는 두번째 주제는 평면도형이다. 아이들에게 평면도형 형태와 관련된 (비교적 단순한) 몇 가지 정보들을 알려 줄 필요가 있다: 삼각형, 정사각형, 원, 각, 직선, 선분이 무엇인지, 또한 그것들을 재어 보는 가장 쉬운 방법을 가르치는 것. 그런데 곰곰히 생각해 보아야할 것이 있다 : 아이가 만약 포크와 숟가락을 쉽게 구별한다면, 삼각형과 사각형을 구별하는게 아이에게 왜 어렵겠는가? 전혀 어렵지 않다! 아이가 실제로 어려움을 느끼는 부분은 개념들 사이의 논리적인 상호관계를 밝히는 것과, 도형의 형태들을 가지고 할 수 있는 활동들을 알아내는데 있다.

아이들은 종종 그게 아니라, 약간 돌려진 정사각형은 그 고유의 상태를 잃어 그냥 사각형이 된다고 생각한다.

11p.

예를 들어, 1학년{첫 해?} 생들 중 많은 아이들이, 정사각형을 비스듬하게 기울여 그린다면, 정사각형은 더 이상 정사각형이 아니라 그냥 사각형이 된다고 생각한다. (그림 1). 그런데, 보통 정사각형이 더 많은가 아니면 사각형이 더 많은가 하는 질문에는 아주 복잡한[여러가지] 논리가 필요하다. 만약 이런 관점에서 문제дело를 바라본다면, 삼각형과 정사각형은[도?] 그 순간 장자상속권??을 잃게된다[삼각형이나 정사각형을 가장 기본[근본]적인 형태라고 할 수도 없다.] : 만약 포크와 숟가락에 대한 문제에 대해서도 뭔가 생각할만한 것이 있다면, 그것은 결코 덜 수학적인 것이라 할 수 없다. 똑 같은 이야기를 좀 다르게 얘기해보자. {초등}학교 수학에서는 숫자와 도형을 가르친다. 그리고 그게 맞다. 그러나 우리는 아이들에게 이런 대상들에 관해 핵심적인 것들을 가르쳐 주는데 있어 너무 많은 것들을 놓친다. 이런 것 때문에 유`아동들이 수학적으로 전혀 발달되지 않을 수도 있다 [유`아동기때 수학적인 발달이 전혀 일어나지 않을 수도 있다]. 그렇게 되지 않게 할 수도 있다. 교구 [재료, 자료]материал들은 너무 많다 {널려 있다}, 필요한 것은 정확하게 (그리고 주의깊게) 문제에 접근하는 것이다.

그렇다면 올바른 접근법이란 어떤 것인가? 여기에 대해서는 사람마다 의견이 다르다. 그 중 몇가지를 소개하려고 한다. (의미를 좀더 분명하게 드러내기위해 과장을 약간 섞었다).

유아와 수학 : 서론 | 제1장 | 제2장 | 제3장 | 제4장 | 제5장 | 제6장 | 제7장 | 제8장 | 제9장 | 제10장 | 맺음말