Set Power Others: 두 판 사이의 차이
편집 요약 없음 |
(차이 없음)
|
2007년 7월 17일 (화) 17:25 기준 최신판
무한 집합의 비교에 대해 알고 싶은 몇가지
알고 싶지 않은 것일수도... :)
손톱만한 길이의 직선과 지구 만한 큐빅 안의 점들은 세기가 같다
잠시 몸을 풀고 ...
몸풀기
몸을 풀 겸, 아래 네 경우에 대해 스스로 풀어보라.
- (0,1) 구간과 양의 실수
- (0,1) 구간과 ()
- () 과 실수 전체
- (0,1) 구간과 실수 전체
이 문제들에 대한 해답은 아래 차례대로.
- 와 의 합성함수
앞에서는 따로따로 보고 있지만, 다음 명제들을 따라가면 충분히 일반적으로 보일 수 있다.
- 직선의 어떤 선분(segment ; 끝점이 닫힌 구간)의 점들도 항상 일대일 대응한다.
- 한쪽이라도 열리거나 닫히거나 상관없이 구간들은 모두 일대일 대응한다.
- 직선의 어떤 구간도 직선 전체와 일대일 대응한다.
이 사실들을 풀기 위해서는 다음의 사실만 확인해보는 것으로 충분하다. 그리고 위의 를 적용하면 된다.
이를 보다 일반적으로 해보면,
- 어떤 무한집합 A 와 유한 집합 B의 합집합은 무한집합 A와 세기가 같다
이다. 왜 그럴까? 집합 A와 B가 겹친다면 당연하고, 겹치지 않는다면 유한집합 만큼 세고 남은 A -B 와 A 를 일대일로 대응하면 된다.
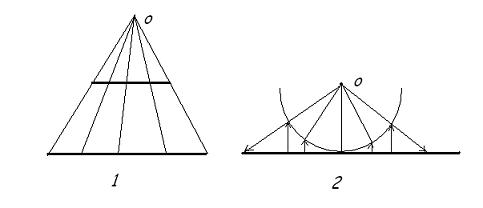
이 사실은 직관적으로 눈으로 볼 수도 있다 : 아래 그림을 보라.
- 구간과 구간 : 열린 구간과 열린 구간의 경우 같은 길이라면 이동해서 나란히 놓은 다음 일대일로 대응시키면 되고, 길이가 다르다면 한 점 O 에서 빛을 쏘아 투영시켜 일대일로 대응하면 된다. (아래 그림 1)
- 구간과 직선전체 : 구간을 반원과 일대일로 대응시킨 다음, 한 점 O 에서 반원에서 직선전체로 투영하여 일대일 대응하면 된다. (아래 그림 2)
여기까지는 그래도 볼 수도 있고 함수적으로도 명확하다. 그런데 다음부터 이어질 사실들은 그저 놀라울 따름이다.
선분과 정사각형과 그 안의 점들은 일대일 대응한다 !
증명 1
자연수와 마찬가지로 모든 실수를 10진법으로 표현할 수 있다. 구간이 [0,1] 이므로 0. 12348383838... 와 같은 실수로 표현될 것이다. 여기에 좌표의 도움을 받으면 모든 정사각형 위 나 안 의 점들을 실수를 나타내는 방법의 도움을 받아 쌍으로 표현할 수 있다. 따라서 우리가 밝히고 싶었던 바는,
- [0,1] [0,1] 과 구간 [0,1] 이 일대일 대응한다.
는 것을 보이면 충분하다. (과연 그런가?) 따라서, 문제를 밝혀내는 열쇠는
을 어떻게
로 나타낼 것인가에 달려 있다. 열쇠를 찾으러가자. 과연 어떤 주문을 걸면 열쇠가 나타날까? 이 문제는 뜻밖에 간단하게 드러난다.(드러나는 것 처럼 보인다.) 아래를 보자.
으로 하면 된다. 우리가 '대응시키고' 싶었던 에 x 좌표에서 한번 다음 y 자표에서 한번씩 차례로 하나씩 골라내 끼워넣으면 된다! 예를들어,
- .
다. 이제 이 '함수'가 과연 일대일로 대응하는지 살펴볼차례다. 일대일 정의를 생각해보면 다음 두가지를 반드시 짚고 넘어가야 한다.
- 정사각형 위나 안에 있는 서로 다른 점들은 선분의 다른 점들로 대응하는가?
- 정사각형 위의 모든 점은 선분 [0,1] 의 모든 점으로 대응하는가?
첫번째 질문에 대한 것은 분명해 보인다. 예를들어 정사각형의 두 점에 대해
이면 대응하는 점들
로, 서로 다르다. (일반적인 경우에도 정말 그럴까? 증명을 말끔하게 완성해보라.) 두번째 질문에 대한 답은 ? (스스로 찾아보라.) 과연 우리는 일대일로 모두 대응시켰을까?
결론부터 말하면, 우리는 정사각형의 점들 모두를 선분의 부분 으로 대응시켰을 뿐이다. 다시말하면,
- 정사각형의 점들은 선분의 점보다 더 셀 수는 없다.
는 사실만 보였을 뿐이다. 하지만, 선분은 정사각형의 부분집합이라 볼 수 있으므로 선분이 정사각형보다 더 셀 수는 없다는 사실에 주목하라. 따라서 두 집합은 세기가 같다.
위의 증명은 직선과 자연수의 대응을 말한 것이기도 한데, 짚고 넘어가지 않을 수 없는 구석이있다. 직선의 점들을 실수와 대응시킬 수 있다하더라도 그것을 '십진법 체계'로 나타내는 데서 오는 문제가 있는 것이다. 이것은 위의 경우 큰 문제가 되지 않는데,정사각형이 이루는 면과 한 직선의 대응에서는 문제가 된다. 물론 풀지 못할 문제는 아니다. 이야기를 간단히 하기 위해 실수 구간 [0,1] [0,1] 에서 [0,1] 로 대응한다고 보자. 먼저 정사각형이 이루는 면에서 선분으로 점들을 일대일 대응시켜보자.
- 일 때,
- x 가 , y 가 이라면 z 를 로 해주면 된다.
일대일 대응이 되었다. (정말 그런가?) 그런데 이때는 선분의 모든 점들을 대응시켰다고 볼 수 없다. (왜 그런가?) 그렇다면 이제는 선분에서 정사각면으로 대응을 시켜야만 완전하게 대응이 이루어진다. 다시 말해 [0,1] 에서 [0,1] [0,1] 로 일대일로 대응시켜야 한다. 보나마나 뻔해보인다. 왜냐하면
- z 가 이라면, x 를 , y 가 으로 대응할 수 있기 때문이다.
그런데 이때 과연 일대일이 성립할까? 이 문제의 단점은 바로 이런 것이다.
- z 가 0. 2000000.... 일 때와 z' 가 0.12929292929... 라고 해보자. 그럴 때 위의 방법으로 하면 z에서 x 로 0.20000... 이고 .z'에서 x 로 0.9999999... 가 된다. 이 수는 같다. 일대일 대응이 되지 않는다 !
- Q : 앞의 경우는 십진법 표기 방법 때문에 생긴 문제다. 이 문제를 어떻게 해결해야할까? [1]
잠깐 !
여기서 잠깐 ! 우리는 이 사실을 증명했는가? 다시 말해 어떤 집합 A 와 어떤 B 가 있을 때,
일까? 유한 집합에서야 당연해보인다지만, 무한 집합에 대해서도 그렇다고 자신할 수 있나? [3]
증명 2
위의 증명은 다른 성질들에 기댈 때 비로소 증명이 완성된다. 그렇다면 과연, 정사각형 위의 점들과 선분의 점들 전부 에 대해 곧바로 일대일로 대응시킬 수 있는 방법이 있을까? 답부터 말하면, 그렇다. 그렇다면, 어떻게 할까? 이를 위해서는 앞의 증명이 왜 전부를 대응하지 못했는가를 따져야 한다. 여기서는 방법만 밝히겠다. 만약 증명 1 에서 멈춰서 꼼꼼히 따져보지 않고 읽은 사람이라면, 이 증명과 위의 증명의 차이가 과연 무엇인지 여기서는 결국 멈추어 생각해봐야 할 것이다. 물론 '증명'의 이해안가는 부분을 바로 넘기겠다면, 더 할 말이 없지만... 증명 1과 비교하면서 보라. 과연 증명1에서 무엇이 못마땅한 부분이었는지 증명 2의 방법을 통해 유추해볼 수 있다.
- 정사각형 위의 점들의 일부인 <x,y> 만 본다. 여기서 0 x < 1 이고 0 y < 1 이다. 다시 말해, 정사각형의 두 변을 빼고 난 대부분의 점들 모두를 [0,1) 전체에 대응시킨다.
- 길이가 3인 선분을 잡아서 그 직선 위의 점을 z 라 하자. 앞에서 빼낸 부분을 에 일대일로 대응시킨다. 이 부분은 이미 앞의 '몸풀기'에서 충분히 익혔던 터라 여기서는 따로 보지 않겠다.
- 그렇다면 이 증명의 첫부분을 보장할만한 알고리듬은 무엇일까?
- <x,y> 의 좌표 중 x, y 에 대해 9가 아닌 수들 다음에 모두 칸막이를 친다. 예를들어 ::::<0,123991 , 0.94949 > 는 <0,1 | 2 | 3 | 991 | , 0.94 | 94 | 9 >
- 다음 그 묶음 들을 앞의 증명에서 했던 대로 차례로 하나씩 연결한다. 예에서 든 것을 해보면,
- 0.1942943999419
가 된다. 이렇게 하면 우리가 바라던 열쇠를 찾아 밝히고 싶었던 성질을 밝혔다.
무엇을 말하고 있는가?
직선의 점들이 정사각형의 점들과 일대일로 대응할 수 있다. 이 놀라운 사실은 곧바로 정사각형 위와 안 점들이 모두 큐빅의 위와 안 점들까지 일대일로 대응한다고 할 수 있다. 그렇다면 이는 '같은 세기'의 기본성질에 따라 직선과 큐빅이 일대일로 대응하고, 우리가 아무리 작은 구간을 잡아도 어떤 선분은 우리가 아무리 크게 상상할 수 있는 큐빅과도 일대일로 대응할 수 있다는 것을 포괄하고 있다. 뿐만 아니다. 단지 2차원과 3차원 뿐만 아니라 4차원, 5차원 과 같이 어떤 차원의 기하학적 도형이 직선을 품고 있다면 그것은 직선과 일대일 대응인 것이다.
위의 사실을 밝혀낸 칸토르를 사실, 1차원인 직선과 2차원인 평면이 일대일로 대응할 수 없다는 것을 보이려고 했다. 1871년부터 1874년 동안 이 '불가능성'을 증명을 찾아내려 했다. 그러나 찾아낼 수 없었다. 1877년 직선과 평면이 일대일로 대응한다는 사실을 밝혔고 스스로 놀랐고 믿기 어려워했다. 왜냐하면 다른 차원의 공간이 '같은' 세기, 다시 말해 일대일로 대응할 수 있다니 ! 1877년 초여름, 데데킨드에게 쓴 편지에는 다음과 같은 말이 있다.
- 눈에 보이지만, 믿을 수가 없군요.
- 수년간에 걸쳐 나는 그 반대라고 생각해왔지만, 내 생각에 이 문제이 대해 그렇다고 말할수 밖에 없습니다. ...
칸토르의 편지를 받은 데데킨드는 이 사실이 '공간의 차원의 문제'와 그리 충돌하지 않는다는 것에 주목했다. 데데킨드에 따르면 차원이 다른 공간이라도 일대일 대응할 수 있지만, 그 일대일 대응이 연속성 을 보장하지 않을 것이라고 추정했다. 다시 말해,
- (정리 : 데데킨드-브라우어) 차원이 다른 공간의 기하학적 도형에 대해 연속성을 보장하는 일대일 대응은 있을 수 없다.
이 가설에 대해 칸토르 스스로 증명을 했지만, 증명엔 잘못된 부분들이 있었다. 여러 사람들이 증명을 시도했지만, 증명은 그리 쉽게 드러나지 않았다. 그러던 중, 1890년 페아노(Peano)는 다음의 흥미로운 사실을 밝혀냈다. 물론 이는 그림으로 그릴 수 없지만, 최대한 비슷하게 나타내면 오른쪽 그림과 같다.

- 직선과 정사각형을 연속으로 대응할 수 있다.
다시 말해, 정사각형의 어떤 점이든 모두 지나되 연속성이 지켜지는 바로 그런 선분이 있다는 것이다. 이를 페아노 선이라고 부른다. 페아노의 발견은 직관적으로 우리가 받아들였던 '차원'에 대한 또 하나의 충격이었다. 직관적으로 분명히 다른 두 도형이 연속성을 유지하면서 대응할 수 있다니 ! 이상한 무한의 세계 2 ; 이상한 함수, 이산한 선 참고하라. (이 선은 한 점을 여러번 지날 수 밖에 없다. 왜 그런가?)
하지만, 이러한 과정을 거쳐서 수학은 점점 한계를 넓혀간다. '차원'의 개념은 이제 '서로 일대일 이면서 연속적일 수 있는 대응' 이라는 새로운 개념으로, 더 확장되고 정확한 정의를 받아들인다. 이에 대해서는 토폴로지 를 참고하라.
사실, 차수가 낮을 수록 서로 다른 차원의 도형들에 대해 연속성을 보장하는 일대일 대응이 없다는 것은 더 쉽다. 그러나 일반적 인 경우에 대해 증명하는 것은 쉬운 일이 아니었다. 칸토르와 데데킨트 이후 30 여년이 지나서야 드디어 브라우어(L.Brouwer)가 증명해낸다.
무한 길이가 가능한 모든 전보들은 실수와 세기가 같다
이상한 무한의 세계 : 무한개의 방이 있는 여관에서 벌어진 일 에서 무한 방이 있는 여관에서 벌어진 일 중 무한 길이까지 칠 수 있는 전보들을 모두 모으면 그것들이 호텔의 방의 개수가 같을까 아니면 다를까 물었다. 전보는 모르스 부호로 치기 때문에 결국 와 - 로 표시된다. 따라서 문제에서의 가능한 전보의 크기는 두 개의 기호를 써서 무한 길이 만큼 나타낼 수 있는 어떤 기호의 열들의 집합과 같다. 이를 다시 말하면 0과 1로 된 무한까지 뻗어 나갈 수 있는 수의 열들을 모두 모은 집합과도 마찬가지다. 모든 실수 집합과 비교해도 되고, [0,1] 구간과 같다는 것만 보여도 충분하다.
핵심은 일대 일로 대응할 알고리름 f 를 찾는 것이다. (생각해보라.)
십진법으로 실수를 나타낸다고 가정하자. 같은 실수에 대해 두가지 표현법이 있는 경우가 있다. 예를들어 1.0000... = 0.99999.... 또는 0.11009999.... = 0.11001000... . 우리는 이 주 9가 반복되어 나타나는 것들은 모두 빼냈다고 가정하자.[4]그리고 일대일 짝지기 알고리듬을 찾아보자.
- 실수란 결국 0,1,2, ..., 8, 9 라는 기호 열 개의 나열들의 모임이다. 그렇다면 기호 열 개를 0과 1 기호의 나열들과 일대일로 짝짓기할 수만 있으면 된다. 0 은 0000으로, 1은 0010로, 2는 0011로, 3은 0101로, ... 8은 1000으로, 9는 1001로 대응하자. (10진법을 2진법으로.) 0과 1로 표현된 수들을 0, 1, 2, 3, ... 으로 바꿀 때는 네 단위로 묶어서 차례차례 번역해주면 된다. 예를들어
- 0.12321... 0000 | 0010 | 0101 | 0011 | 0010.....
그리고 서로 다른 실수는 서로 다른 0과 1의 기호의 열로 표현될 수 밖에 없다는 것을 보인다. 다시 말해 10진법과 2진법 서로 표현을 바꾸어주는 알고리듬을 쓰면 된다.
이 뿐만 아니다.
- 자연수의 모든 부분집합들의 집합과 무한길이 전보들의 집합도 대등하다.
- 비어있는 집합은 0000... 으로, { 1 } 은 10000... 으로, { 1, 2 } 는 11000... 으로 짝수들 집합은 01010101... 홀수들의 집합은 101010... 으로 바꾸주면 된다. ( 알고리듬을 어떻게 한 것인가? )
사실 이것은 그리 놀라운 사실이 아니다. 왜냐하면 무한길이 전보들을 모두 모으면 '셀 수 없다' 그리고 자연수의 모든 부분집합들의 집합도 셀 수 없는 집합이기 때문이다. 증명은 실수집합을 셀 수 없다는 것을 증명했던 '대각선 방법'으로 보이면 충분하다. (스스로 해보라.)
Note
- ↑ 우선 하나의 숫자는 한가지 방식으로만 표기하는 것으로 약속을 해서 9가 연속해서 끝없이 등장하는 경우를 배제하는 방법이 가능할 것이다. 그래도 여전히 문제는 남는다. 어쨌든 위의 '쪼개서 담는' 방법으로는 0.12929292929... 같은 숫자를 대응시킬 수 없는 경우가 나타날 수 밖에 없을테니까. 이 문제는 이렇게 해결할 수 있다. 하나씩 하나씩 세지 않고, 덩어리 단위로 쪼개 모으면 된다. 이렇게...
- 0.12929292929... 를 0.(1)(2)(92)(92)... 로. 다시 말해 9로 시작해서 그 다음 9가 안나올때까지 한 덩어리로 묶어가는 것이다. 그런 다음 덩어리 하나씩 하나씩. 예를들어 0.239976432349923959... 는 0.(2)(3)(997)(3)(4)(992)(3)(95)(9...
- ↑ 기호 는 집합 A 의 세기보다 집합 B 의 세기가 '크거나 같다'를 뜻한다.
- ↑ 우리는 지금까지 보았지만 무한 집합의 성질은 유한 집합의 성질과 다른게 무척 많았다. 사실, 이것은 그리 어려운 문제가 아니라 해도 이것과 관련해서 집합론에서 다루는 기초적인 정리가 있다. 정리만 옮기면 이렇다.
- 집합 A 가 집합 B 의 부분집합과 크기가 같고, 집합 B 가 집합 A 의 부분집합과 크기가 같으면,
- ↑ 그것들의 개수는 몇 개나 될까? 무한일텐데 어느 정도나 셀까? 셀수 있는 정도 있까? 연속체일까?
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia














![{\displaystyle x\in [0,1],\ y\in [0,1],z\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91fa34d4f609fc832a3aa7f06ee243778dabffdf)













