Child Math:23

활동 23. 하노이의 탑

• 일시 : 1981년 2월 28일(토요일). 10시40분-11시15(35분).
• 참여 : 지마, 줴냐, 뻬쨔, 안드류샤.

과제 1. 이행성(transitiveness)에 대한 구술 질문

이행성

안드류샤에게:

한 아이가 아이스크림을 호두보다 더 좋아하는데, 호두를 오렌지보다는 더 좋아해. 그럼 아이는 무엇을 더 좋아하는 걸까 ? 아이스크림일까, 오렌지일까?

- 아이스크림요.

왜?

- 왜냐하면, 걔가 아이스크림을 더 오래전에 먹기 시작했잖아요.

걔한테 먹도록 한게 더 오래되어서 그렇다는 말이니?

- 네.

지마에게:

할아버지가 아빠보다 돈이 더 많아, 그리고, 아빠는 엄마보다 돈이 더 많고. 그럼 누구한테 돈이 더 많은 걸까 ? 할아버지니, 엄마니?

-할아버지요.

왜?

- 할아버지가 엄마보다 돈을 더 많이 버시는걸 제가 알거든요.

그걸 어떻게 알았어?

- 그냥 알아요. 그게 단데.

그럼, 문제을 풀어 안거니, 살면서 아는거니?

- 살면서요.

줴냐에게:

소나무가 전나무보다 더 크단다. 전나무는 자작나무보다 더 크고. 그럼 어떤 나무가 더 클까 ? 소나무일까 자작나무일까?

-소나무요.

왜?

줴냐가 뭐라고 대답했는지는 기억이 안난다. 그런데 지마가 끼어들며 말했다: -왜냐하면 소나무는 제일 큰 나무고, 자작나무는 제일 작은 나무잖아요. 전나무는 제일 중간 나무고요.

정말 그런건지, 손짓발짓하면서 자기네들끼리 의논을 한다.

(줴냐가 뭐라고 말했는지 기억이 났다: -소나무가 자작나무보다 더 먼저 자라기 시작했잖아요.

<<왜?>>라고 내가 물었던 것이 아이들에게는 <<그건 왜 그렇게 되었지?>> 를 설명하라고 요구하는 것으로 받아들였는지 모른다. 소나무가 자작나무보다 크다는 것은 논리적 결과인데, 거기서 벗어나 왜 더 큰지 설명하려고 한 것이다. )

뻬짜에게:

물은 찻주전자보다 냄비에 더 많이 들어가, 그리고, 물병보다는 찻주전자에 더 많이 들어가고. 그럼 어디에 물이 더 많이 들어갈까-냄비일까, 물병일까?

-냄비요.

왜 그렇지 ?

또 지마가 간섭을 한다, 그리고는 뻬짜와 함께 설명을 하는데, 다 맞는 말이다.

[조건이 사실과는 다른 것으로 한번 물어볼 필요가 있다 : 예를들면, <<줴냐가 지마보다 커, 지마는 아빠보다 크고. 그럼 누가 더 크지 - 아빠일까 줴냐일까? ]

과제 2.

지난 번처럼, 다시 책상에 정사각형과 직사각형, 그리고 사각형이 있다. 그 이름들을 상기시켜 본다. 그리고는 책상 위에 정사각형은 몇 개 있고(한 개), 직사각형은 몇 개가 있으며(두 개), 사각형은 몇 개가 있는지(세 개) 세어보라고 한다. 마지막 질문에 뻬짜 혼자만 옳게 대답한다. 마지막에는 결론적인 질문을 한다:

그럼 뭐가 더 많은 거지 - 정사각형이니 사각형이니?

결과는 같다. -정사각형요. (왜냐하면 집이나, 지붕이나, 파이프나 기타 등등 어디에도 정사각형이 더 많기 때문이다).

나는 아무 설명도 해주지 않고, 정사각형이 사각형이냐고 묻기만 한다. 대답은: -네.

과제 3.

<<1학년 수학 교구 모듬>>에서 열여섯개를 골랐다. 이 개수는 참여한 아이들의 네 배수로 한 것이다. 그것들은 파란색 원 2개, 노란색 정사각형 2개, 빨간색 삼각형 4개, 녹색 삼각형 5개다. 끝을 이어 놓은 끈을 책상 위에 빙 둘러 놓는다. 아이들에게 하나씩 차례로 나누어 준다. 끈 안쪽에는 빨간 것을 놓아야 하고, 바깥쪽에는 빨간색이 아닌 것을 놓아야 한다.

끈을 치운다. 똑같이 생긴 다른 끈을 놓는다. 이젠 안쪽으로 삼각형을 놓고, 바깥쪽에는 삼각형이 아닌 도형을 놓아야 한다. 안드류샤가 실수 하나 했지만, 모두 제대로 다루었다.

마지막에는, 잠시 두 끈이 겹치지 않도록 책상 위에 둔다. 그러고는 한꺼번에 두 과제를 풀게 한다. 한 번 돌았을 때 (처음으로) 빨간 삼각형을 은근슬쩍 일부러 지마에게 준다. 지마는 생각할 겨를도 없이, 그것을 빨간색이 들어가야 할 곳에 놓는다. 충돌되는 조건들이 있다는 것을 모두에게 환기시키고, 이 문제를 풀어야 한다고 말해준다.

[또 서두르네! 끝까지 기다렸다가, 그 다음에 다 맞는지 이야기 나누었어야 했는데.]

안드류샤 왈:

-이거, 일부러 이런 거예요?

-물론 일부러 그랬지. 지금까지는 준비단계였단다. 진짜 풀어야하는 건 이제부터야. 이 삼각형이 여기인지 저기인지 놓이도록 어떻게 생각 좀 해내야 할 것 같구나.

지마가 삼각형을 두 끈에 다리처럼 걸쳐 놓으려고 한다. 그래서 내가

- 어떻게든 끈을 움직이지는 않을까 ?

끈 하나를 다른 끈 위에 놓아야 한다는 것을 안드류샤가 제일 먼저 짐작해서 말했다. (지마도 눈치채긴 했는데, 미처 말을 못한 것 같다.)

P. 41

이제 다 풀린 것이다. 끝까지 마무리를 짓는 것은 어렵지 않다. (빨간색 삼각형이 다해서 4개니까, 누구나 한번씩 빨간색 삼각형을 받게 된다). 검정색 책상 위에 흰 색 끈과 여러 가지 색깔의 도형들이 참 예쁘다. 아이들에게도 이걸 얘기해주었다.

-이거 내가 생각해낸 거다!

안드류샤 그렇게 말했다. 그러자 지마가

-무슨 소리야. 내가 생각해 낸거야!

란다.

빨간색 삼각형이 두 모임에 동시에 속하는 것에 대해 뭔가 좀 더 이야기하려 했지만, 소용이 없었다.

과제4. 하노이의 탑

모두에게 놀이 도구를 하나씩 나누어주고, 놀이 규칙을 설명해준다.

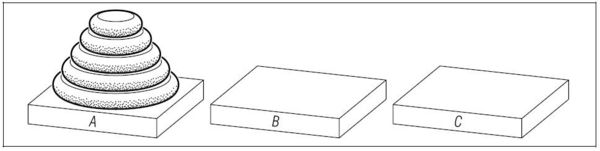
이 놀이는 프로그래머를 위한 읽기 자료에서 주옥으로 여겨진다.  : 이 놀이는 5세 아동부터 할 수 있으면서도, 정보학 관련 대학원생들에게도 생각할 거리를 준다. 처음엔 여러 색깔의 원반 몇 개가 탑처럼 쌓여있다. 세 판 중 하나에 이 탑이 쌓여있는 것이다. (그림 15).

(그림 15) 시작 상태의 하노이의 탑

아래 규칙을 지키면서 다른 판으로 탑을 옮기는 것이 놀이의 목표다.

(a) 원반들은 판에서 판으로만 옮겨질 수 있다 ; 이 때 원반들이 겹쳐져 놓이게 되면서 작은 탑 모양이 된다. 원반을 어디 다른 데로 빼놓아서는 안된다;

(b) 한 번 옮길 때마다 하나의 원반만 움직일 수 있다 - 여러 개의 원반을 한번에 옮겨서는 안된다: 특히, 양손에 하나씩 원반을 쥐어서도 안된다.

(c) 원반은 어느 탑이든 꼭대기에 있는 것만 뺄 수 있다, 그리고 그 원반도 다른 탑의 맨 위에만 얹을 수 있다; 다시 말해, 탑 중간에 있는 원반을 빼서는 안되고, 그것을 다른 탑의 중간에 끼워 넣어서도 안된다(이 규칙을 더 분명히 하기 위해 보통 중심에 구멍을 뚫은 원반을 준비해서 그것을 막대기둥에 끼워 탑모양을 쌓을 수 한다. ) ;

(d) 마지막으로 절대 큰 원반을 작은 원반 위에 놓아서는 안된다. 이 규칙은 아주 중요하다.

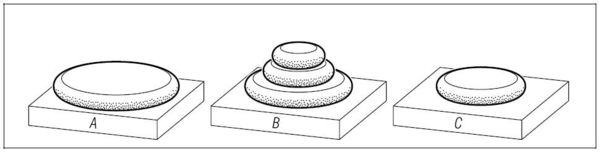
그림 16은 게임이 진행 중의 한 과정을 보여주고 있다.

(그림 16) 게임 진행 중의 한 과정에 있는 탑. 게임의 마지막에는 탑이 옆의 다른 판들에서 B판이든 C판이든 어느 한 판으로 완전히 옮겨져야 한다.

이 게임은 19세기 프랑스 수학자 에두아르 뤼크가 고안했다. 그는 낭만적인 전설로 이 놀이를 꾸몄다.

하노이에서 멀지 않은 어딘가 울창한 정글에 브라마의 수도원이 있다. 브라마가 세상을 창조했던 태초에, 브라마는 세계의 높은 다이아몬드 기둥을 세웠고, 그 중 하나에 64개의 황금 원판을 끼워놓았다. 그는 수도승들에게 이 탑을 다른 기둥으로 옮기라 명령했다 (물론, 모든 규칙을 지키면서 말이다). 그때부터 지금까지도 수도승들은 밤낮으로 옮기고 있다. 그들이 탑을 완전히 옮기면 세상은 종말을 맞게 될 것이다.

좀 더 나이가 찬 아이들을 위해 이 <<세상의 종말>>이 언제 올지 대충이라도 계산해보는 문제를 따로 낼 수 있다. [귀뜸: n 개의 원판이 쌓인 탑을 옮기기 위해서는$2^{n}-1$ 번 원판을 이동해야 한다. 만약 하나의 원판을 옮기는데 일 초가 걸린다 하자. 그럼 n = 64일 때 이 탑을 다 옮기는데 시간이 얼마나 걸릴까?]

이 작업을 하는 동안 아이들 모두를 다 보고 있기는 정말 벅찼다. 아이들은 이 규칙을 계속 어겼다.

지마는 이미 두 번이나 이 놀이를 해봤다. 그래서 제일 빨리 끝내고, 규칙도 어기지 않았다. 모두 막다른 골목에 다다랐던 끝 무렵에 지마가 자신감에 차서 척척 해내는 것을 숨죽이며 쳐다보았다.

뻬짜는 나와 지마와 나타샤가 도와줬는데도, 규칙을 받아들이지 못했고, 끝까지 규칙을 어겼다. 뻬짜는 지마가 귀뜸을 해주는 것에 화를 냈다.

줴냐는 규칙은 이해했지만, 극도로 어쩔줄 몰라했다. 거의 내내 위에 놓인 원반 두 개를 꺼내서는 어떻게 해야 할지 모른 채 앉아만 있었다. 나타샤와 지마와 내가 그 애를 도와주었다. 줴냐도 지마가 방해를 하니까 잘 안되는 거라면서 지마에게 화를 냈다. 지마가 애들을 무시하면서 말하기를, 줴냐나 안드레이보다 뻬쨔가 더 먼저 해내라고 일부러 뻬짜를 도와준거라 했다. 그리고, 다른 애들은 다하고 놀고있는데, 줴냐는 계속 앉아있기만 할 것 같으니까 도와준거라 했다. 지마에게 엄한 주의를 주어야 했다.

안드류샤는 내가 미처 못보았는데, 무척 빨리 해냈다. 내가 했더라고 그렇게 빨리는 못했을 것이다. 안드류샤에게 다시 한번 해보라고 부탁했다. 그러자 뭔가 제대로 하지 않은 걸 아는 듯, 제일 먼저 해결했으니 되풀이는 안할거라며 딱 잘라 거절했다. 그래서 내가 말하기를:

안드류샤, 내가 생각하기에는 네가 규칙을 어긴 것 같은데?

- 내가 언제요?!

내가 아무것도 못봤기 때문에 잘못을 밝힐 수 없다는 걸 알고서 뻔뻔스럽게 소리친다.

그런데 이때 류다가 아들 안드류샤를 배신하고 잘못을 말했다. 안드류샤는 아주 풀어죽어버렸다. 류다가 안드류샤를 위로한다고 규칙대로는 어떻게 하는지 보여주려했는데, 결과적으로는 류다 혼자 다 해버린 셈이 되었다. 뻬짜가 게임을 끝냈을 때 안드류샤가 말했다.

- 근데, 힌트를 진짜 많이들 주니까 뻬쨔가 해낸 거란 말예요.

자신은 아예 손도 못대다시피 한 걸 까맣게 잊어버리고서는 말이다. 그러고는 줴냐에 대해서도 뭐라 탓하려고 한다.

이런 행동에 대해, 어린 아이들의 행동으로 봐줘야하는데 마치 어른이 그렇게 한 것처럼 반응한다는 건 내 단점이다. <<아이가 아니라, 아이의 행동을 야단쳐라>>는 원칙을 이론상으로는 알고 있지만, 현실적으로는 먼 나라 얘기다. 가장 중요한 점은, 내 자신의 기분이 상하고, 그것이 아이들의 어처구니 없는 행동보다 훨씬 전체 분위기에 영향을 더 준다는 것이다.

유아와 수학 : 서론 | 제1장 | 제2장 | 제3장 | 제4장 | 제5장 | 제6장 | 제7장 | 제8장 | 제9장 | 제10장 | 맺음말