Fagnano Schwartz Problem

18세기의 이탈리아의 수학자이자 과학자 판야노는 다음과 같은 문제를 던졌다.

어떤 예각삼각형의 세 변에 꼭지점을 둔 삼각형 중 그 둘레가 가장 작은 삼각형은 어떤 삼각형일까?

과연 모든 예각삼각형에 대하여 '일반화된' 답이 있을까? 다시 말해 예각삼각형이 주어지기만 하면 우리는 그 삼각형을 찾아낼 알고리듬이 있을까? 하는 문제다. 다행히 답은 긍정적이었다.

어떤 예각삼각형의 세 변에 꼭지점을 둔 삼각형 중 그 둘레가 가장 작은 삼각형은 altitude triangle^[1]이다.

altitude 삼각형 이란 주어진 삼각형의 꼭지점에서 수선을 내려 반대편 변과 만나는 점(높이) 들 셋을 이은 삼각형을 말한다.

이 증명 또한 여러가지가 있다.

증명 1 : 삼각형의 변에 대칭

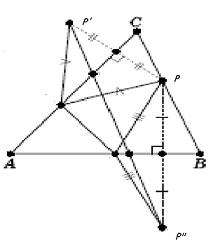
주어진 예각삼각형 ABC가 있을 때, 세 변에서 한 점 씩 선택해서 이를 이어 얻은 삼각형 PQR 를 보자.

변 AC에 P가 대칭인 점을 P'라 하고, AB에 대칭인 점을 P"라 하자.
꺽인선 P'BCP" 길이는 삼각형 PQR 의 둘레와 같다.
따라서 정해놓은 P 를 놓고 볼 때, 선분 P'P"와 AC, AB 가 만나는 두점들과 P 가 이루는 삼각형의 둘레가 가장 작다.
이제 선분 P'P"의 길이가 최소가 되도록 하는 P 는 어떤 조건에 있는 점일까를 생각해봐야 한다.
먼저, 점 P 가 선분 BC 의 어디에 있든지 삼각형 P'AP" 은 이등변 삼각형이고, 그 각은 각 BAC의 두배라는 사실을 주목하자. (왜 그런가?)
그렇다면, 선분 AP' 의 길이가 최소가 되도록 잡으면 선분 P'P" 의 길이도 최소가 될 것이다.
다시 말해, 선분 AP 의 길이가 최소가 되도록 점 P를 찍으면 된다. 그 조건을 만족하는 것은, 물론, A 에서의 높이의 발이다.
임의로 찍은 점 Q 와 R 에 대해서도 마찬가지 방식을 적용하면 B 와 C 에서의 높이의 발이다.

이 증명은 Heron 정리의 증명에서처럼 '대칭' 개념 말고는 특별한 기하적 변환은 쓰이지 않았다.

증명 2 : Schwartz의 증명

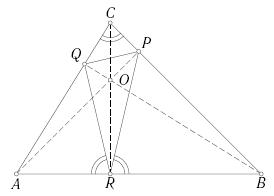
먼저, 다음을 밝혀보라.

삼각형 ABC의 변이 이상적으로 편평한 거울이라고 하자. 그 때 altitude 삼각형의 어떤 점에서 그 변을 따라 빛을 쏘면 그 빛은 영원히 altitude 삼각형을 벗어나지 않는다. 다시 말해 빛이 삼각형 ABC의 한 변에 부딪히면 그 변과 들어오는 빛이 이루는 각과 나가면서 이루는 각은 같다. (옆의 그림에서, 예를들어, 각 PRB = 각 QRA)

(증명) 예각삼각형 ABC의 꼭지점에서 높이를 이루는 세 점을 P, Q, R 이라고 하자. 각 PRB = 각 QRA , 각 PQC = 각 RQA, 각 QPC = 각 RPB 임을 보이면 된다. 첫번째만 보이기로 하자.

세 꼭지점에서 높이(수선)들이 만나는 한 점을 O 라 하자.
OB를 지름으로 하고 P, R을 지나는 원을 작도한다.
각 PBO = 각 PRQ (현 PO를 공유하고 있는 각들이기 때문.)
각 C = 각 PRB = 90 이고, 각 PRO + 각 PRB = 90 이므로 각 C = 각 PRB
OA를 지름으로 하고 Q, R을 지나는 원을 작도하여 위와 마찬가지로 하면 각 C = 각 QRA
따라서 각 PRB = 각 QRA
마찬가지 방식으로 하면 나머지 각 PQC = 각 RQA, 각 QPC = 각 RPB 에 대해서도 보일 수 있다.

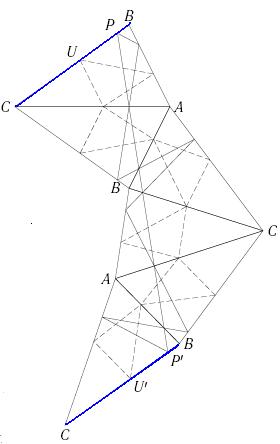
(증명) PQR이 이루는 삼각형은 삼각형 ABC의 altitude 삼각형이다.

주어진 삼각형 ABC와 altitude 삼각형 PQR과 삼각형 ABC에 각 변에 꼭지점을 둔 다른 어떤 삼각형 UVW를 생각해보자.
이 삼각형을 AC에 대해 대칭한다.
새로 얻은 삼각형을 다시 AB에 대해 대칭한다.
새로 얻은 삼각형을 다시 BC에 대해 대칭한다.
새로 얻은 삼각형을 다시 AC에 대해 대칭한다.
새로 얻은 삼각형을 다시 AB에 대해 대칭한다.
앞에서 밝힌 각의 대칭성 때문에 결과적으로 얻은 도형은 오른쪽 그림과 같이 6개의 합동인 삼각형이 서로 변을 마주대고 있고 처음의 BC와 마지막 BC가 평행하다.
이때 선분 PP'는 삼각형 PQR의 둘레의 두 배다.
다른 어떤 삼각형 UVW의 둘레의 두배는 UU'다.
항상 다음 관계가 성립한다 : 선분 PP' < UU'

증명 3 : Heron 정리의 이용

(애벌 증명 )

주어진 예각삼각형 ABC 에 대하여 꼭지점이 아닌 각 변에 둘레가 최소가 되는 P, Q, R 이 있다고 하자.
- 두 점 P, Q 가 직선 AB가 나누는 평면의 한쪽에 있으므로 이 두 선분의 길이가 최소가 되는 점 R에서 이루는 각은 같다.
- 그럴 때, 각 ARQ = 각 QRA = 각 C ; 각 AQR = 각 B ; 각 RPB = 각 A 다.
- 이런 성질을 갖는 삼각형은 altitude 삼각형이거나, 그것과 닮은 꼴인 삼각형이다.
- 삼각형 ABC의 변마다 한 꼭지점을 둔 경우는 altitude 삼각형 밖에 없다.

위의 증명은 아직 충분하지 않다. 왜냐하면 세 점 P, Q, R이 모두 '꼭지점이 아닌' 변에 있는 경우만을 본 경우다. 세 점 중 하나가 꼭지점과 같은 경우 Heron 정리를 쓸 수 없다. 우리는 사전에 이 P, Q, R의 위치에 대하여 반드시 꼭지점이 아닌 변에 위치해야 한다고 할 이유가 없기 때문이다. 따라서 앞에서 살피지 않은 다른 경우도 보도록 하자.

주어진 예각삼각형 ABC 에 대하여 꼭지점 C 에 한 점이, 예를들어 P가, 있다고 하자.
- 그럴 경우 그 삼각형의 둘레는 상응하는 높이의 두배로 접근한다. (삼각형 ABC가 예각삼각형에서 점점 직각삼각형으로 되어간다고 생각해보라.)
- 따라서 altitude 삼각형의 둘레는 가능한 세 높이 중 어떤 높이의 두배보다 작다는 것을 보임으로써 증명은 끝난다.
- WIM 그림 201 참조.

Note

↑ 또는 orthic triangle라고 부른다.

[1] 또는 orthic triangle라고 부른다.

[1]