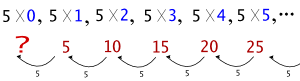Math Mail 06
안녕?
부산은 우리나라 동쪽 끝에 있는 도시지? 삼촌이 사는 청사포는 부산에서도 동쪽 끝에 있어. 동쪽 끝에 동쪽 끝. 실제로 걸어보면 꽤 넓지만. 우리나라 지도를 보면 동남쪽 구석에 있는 한 점 같아. 여긴 벌써 벚꽃이 활짝 피더니, 성급한 녀석들은 벌써 바람에 날리더구나. 어제 밤에는 또 비가 왔단다. 어서 날려 땅에 닿고 싶었던 녀석들은 비를 맞고는 어떻게 되었는지 모르겠구나. 주말 잘 지냈니? 삼촌은 수학과 함께 춤을 췄단다. 공리 체계 라는 단어가 핵심이었는데, 그건 삼촌이 모스크바서 공부할 때 자주 만났었지. 돌아와서는 이런저런 사정으로 덜 만났는데, 오랜만에 흠뻑 빠져있었단다. 아주 재미있는 내용이었지만, 생각에 생각을 거듭하다보니 나중엔 골치도 아프더라. 너무 무겁게 해석했나봐.
이 편지도 혹시 지나치게 무겁게 이야기를 해서 괜시리 우리 명훈이가 읽기 부담스러운 것은 아니니? 그렇지 않길 바라지만 그걸 조절하기가 어디 쉽나. 얼굴 마주하고 대화를 나누지 않은 채 이렇게 일방적으로 써서 보내니 더 그래. 쉽게 설명해보려고 하지만, 뺄 수 없는 것들이 있어서 함께 말하다 보면 얽히고 설키는 게 아닌가 싶어. 어려우면 이야기 해다오. 삼촌이 더 조심할께. 지금은 삼촌이 쓰고 싶은 대로 계속 써나가 보고록 하기로 하고 말야.
지난 시간에 문제 몇 개를 던졌지? 그 질문 중 제법 심각한 게 있었어. 되돌아 보자. 곱셈을 이해할 때, a 곱하기 b 가 a 를 b 번 곱한다 라는 뜻이라면,
들은 모두 0 을 그만큼 더한다는 말이니까, 모두 0 이라는 사실은 받아들여져. 그런데 문제는 이런 경우였어.
이럴 땐 어떻게 해야하지? 참 난처해. 덧셈으로 곱셈을 정의해서 받아들이면 이런 묘한 문제가 일어나. 이런 일은 0 과 만났을 때만 일어나는게 아니야. 나중에 음수(negative number)를 다룰 때도 그렇게 되고 수의 세계를 더 넓힐 때도 그래. 꼭 곱셈에게만 그런 일이 일어나는 게 아니고 말야. 그래서 이 문제를 여기서 짚고 넘어가지 않을 수 없구나.
이렇게 이해하고 받아들일 수 있어. 지금으로서는 받아들일 수 밖에 없을거야. 받아들일만한 근거를 말해 볼께. 먼저, 하나. 우리가 살아가면서도 종종 있는 경우야. 어떤 것을 이해하기 위해 그것만 보는 게 아니라, 그것 주위에 있는 것들과의 관계 안에서 보는 방법 ! 명훈이를 알기 위해서는 명훈이를 잘 만나 봐도 되겠지만, 명훈이 친구들이나 동생 원일이랑 관계, 또는 엄마나 아빠, 마을 사람들이 어떤 성격을 하고 있는지 보면 조금 윤곽이 잡히기도 하잖아. 바로 그거랑 비슷해.
|
이렇게 보면 어떨까 해. 예를들어 을 보자. 이것만 보는 게 아니라, 고개를 들어 두루두루 한 번 둘러보자꾸나. 먼저, 까지 보자. 처음 5가 있는 것은 같고, 오른쪽에서 왼쪽으로 보면, 5, 4, 3, 2, 1 로 1 씩 줄고 있지? 그렇다면 0 도 참여할 때, 그것은 어디에 쓰는게 자연스러울까? 그렇지, 이렇게 쓰겠지. 이제 그것이 곱셈에는 어떤 영향을 주니? 그렇지? 5씩 줄면서 오고 있잖아. 그렇다면 제일 처음에 있던 은 무엇일까? 그렇지 아주 특별한 경우가 아니라면 0 인게 자연스럽지 ! |
'전체 틀' 안에서 볼 수도 있어. 그 전에 먼저 어떤 자연수건 상관없이
는 받아들일 수 있겠니? 쉬어 보이지? 예를들어,
이듯, 다른 어떤 자연수에 대해서도 덧셈하는 두 수의 순서는 상관없어 보이지. 그런데 정말 그럴까?
일까? 이것을 검사해보긴 정말 어려워. 숫자를 제대로 바꾸어 쓰기 조차 쉽지 않아. 제대로 바꿔 쓰긴 썼니?
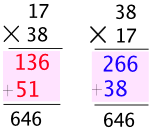
어때? 게다가 옆의 그림을 보자. 우리가 흔히 하는 곱셈 방법으로 했어. 셈의 중간 과정인 빨갛게 칠한 부분만 보자. 이 부분들의 수만 빼내면,
이잖아. 이 결과가 같다는 어떤 징표도 안드러나있어. 그런데 곱셈도 교환이 된다고? 믿을 수 있니?
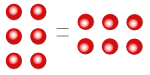
이것도 믿을만한 이유를 말해볼께. 옆의 그림을 보면 나왔듯, 둘을 세 번 곱한 것을 직각으로 회전하면 셋을 두 번 곱한 것과 같지. 그 점의 개수가 변했다고 보기는 어렵잖아? 두 자연수의 곱셈은 무엇을 먼저하건 상관없다는 것을 '빨간공' 을 예로들어 설명해 본 거야.
하지만, 이에 동의하지 않을 수 있어. 물론이야. 받아들이거나 받아들이지 않거나 그건 명훈이의 자유. 대신 댓가를 치러야지? 안받아들이면 곱셈할 때 교환이 안된다고 보게 되고 그러면 곱셈할 할 때 굉장히 어려워질 뿐더러, 앞으로 우리가 전개해 갈 수학은 거의 못하게 될거야. 다른 수학, 분명히 몹시 '가난한' 수학이 될 걸. 이것이 심각한 일일까 아닐까. 받아들일만한 이유가 있으니 받아들이고 할 수 있는 것을 발전시켜 가는 것이 좋을까? 의심에 의심을 거듭하면서 아무 것도 하지 않은 것이 좋을까?
답하기는 만만하지 않지만, 어쨌든 삼촌은 지금까지 인류가 해온 것처럼 자연수에 대해 곱셈도 교환이 성립한다는 수학을 할께. 명훈이가 수학을 잘 이해해서 그 안에 있는 아름다움을 느끼고, 잘 생각하는데도 도움을 하기 위해 공부하는 것이니까.
이제 삼촌이 할 말을 받아들이면 5 곱하기 0 의 결과는 0 이라는 것도 받아들이는 데 큰 무리는 없어. 왜냐, 더 말을 해볼께.
|
자연수에서는 곱셈에 대해 어떤 수를 먼저 하건 상관없다는 수학을 하고 있어. 그렇다면 거기에 0 까지 하나 더 포함시킨, '더 확장된' 수를 보자. 그렇다면 자연수에서만 통했던 법칙이 여기서도 일관성있으면 좋잖아. 그런 관점에서 본다면, 인 것을 받아들이는 게 자연스럽겠지? 이때 조심할 것은 a , b 는 단지 자연수이기만 한 것이 아니라, 0 일 수도 있다는 거야. 덧셈과 곱셈할 때 자연수에 신비로운 수 0 을 포함시켰더니 자연수 세계에서 통하던 법칙이 흐뜨러지면 이상하겠지? 그래서 이고, 99가 아닌 다른 수들에 대해서도 그럴 거야. 더 나아가, 지금까지 우리에게 있는 어떤 수 a 에 대해서도, 가 될거야. 다시 말하지만, 여기서 a 는 0, 1, 2, 3, 4, 5, ... 어떤 수든 상관없어, 알았지? |
이제 어떤 수에 0 을 곱하는 문제까지도 나름대로 해결했네. 그와 함께 자연스럽게 곱셈의 교환 법칙 까지 이야기했어. 곱셈에는 그런 성질만 있는 게 아니지? 덧셈에서 했듯, 자연수와 0 까지 있는 수 세계에서는 , 곱셈만 여러 번 해야할 때 어떤 순서로 곱셈을 해도 상관없다 는 성질이야. 그와 비슷한 것이 덧셈의 결합법칙이라고 했지? 그렇듯,
가 되고, 이것을 자연수와 0 의 세계에서 곱셈에 대해 결합법칙 이라고 부르곤 해. 아주 좋아. 그래서
을 계산할 때, '어떤 곱셈부터 먼저 하는 것이 옳지? ' 라는 걱정은 하지 않아도 돼. (이게 안된다면 앞의 경우, 최대 몇 개 달라질 수 있을까? ?) 이것도 그냥 자연스럽게 받아들이기로 하자. 다시 말하면, 결합 법칙도 성립하는 곱셈을 우리는 할 거야.
자, 그럼 곱셈을 어떻게 하는지 그리고 곱셈은 어떤 기본적인 성질이 있는지 보았다. 곱셈에 대한 이야기를 끝내기 전에 하나만 더 이야기를 하고 싶구나. 명훈이도 그렇고 대부분의 현대인들은 곱셈을 어렵지 않게 해내지. 초등학교만 잘 마쳤어도 곱셈을 어렵다고 생각하지는 않을거야. 그런데 옛날 사람들은 달랐어. 숫자 표기가 자릿수법으로 바뀌고, 0 이 수로 인식되고 기호 열 개가 정해지면서, 다시 말해서 10진법이 자리를 잡아가면서야 비로소 곱셈은 쉬운 셈이 되었던 거야. 그런데 불과 몇 백년 전까지도 5 곱하기 0 과 같이 0 이 곱셈에 참여하면 사람들은 무척 어려워했단다. 뿐만 아니라 음수나 0이 아닌 수에 대해서도 곱셈과 나눗셈은 아주 어려웠어. 곱셈과 나눗셈을 잘 해야하는 상인들은 그것을 잘 배우기 위해 자식들을 외국 유학 보낼 정도였단다. 놀랍지 않니? 이 모든 것이 10진법 체계가 자리잡기 전의 일이야. 10진법 체계가 자리를 잡아가면서 이것은 어렵지 않은 게 되었어. 여기에 꼭 말해야할 것이 곱셈을 하는 '좋은 알고리듬'이 개발되었기 때문이야.
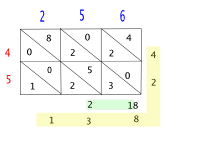
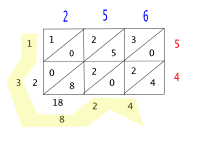
곱셈을 항상 우리가 하는 방식으로 했던 게 아니거든. 곱셈하는 방법도 많았어. 무엇이 더 나은 방법이냐 가지고도 알게모르게 오래 경쟁했어. 아래 몇 개 예를 볼거야.
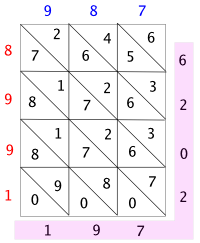
우선, 꽤 많이 썼던 방법을 보자. 같은 곱셈인데, 그것을 하는 '알고리듬'이 달랐어. 불과 조선시대 사람들만 해도, 만약, 256 곱하기 54를 할 때는 오른쪽 표처럼 했단다. 숫자가 세 개 있는 자연수와 두 개 있는 자연수를 곱셈할 때, 2 곱하기 3의 개수 만큼 네모 칸을 만들어. 그리고 그 네모 칸을 모두 대각선으로 나눠. 그리고는 숫자 하나 하나씩 곱셈을 해서 결과는 적었지. 구체적으로 어떻게 했을까? 시시콜콜 적지 않을께. 옆의 표를 보면 명훈이 스스로 알 수 있겠지? 이때 54는 아래서 위로 썼다, 조심해서 보거라. 꼭 그렇게 해야하는 건 아니지. 표의 아래에는 같은 방법인데 왼쪽과 오른쪽을 달리 해 보았어. 그러면 54를 쓰는 것도 위에서 아래로 써야지. 잊지 않아야 할 것은 '10진법의 곱셈표'를 외우고 있었야만 했다는 사실이야.
또 다른 곱셈도 있어. 여기서 설명은 하지 않을께. 재미있는 동영상이 있는데, 곱셈하기 동영상 을 보겠니? 재미있을거야. 이런 방법은 놀랍게도 10진법의 곱셈표를 외우지 않아도 된다는 장점이 있지? 그렇다면 왜 이 방법으로 통일이 안되고 곱셈의 알고리듬은 지금 우리가 하는 방식으로 자리를 잡아가고 있을까? 생각해보고 공책에 적어보겠니?
아래에는 같은 곱셈인데 여러 방식으로 해봤어. 지금까지 안본 알고리듬도 있어. 모두 1998 곱하기 987의 곱이야. 제일 마지막 것이 우리가 흔히 쓰는 알고리듬. 그럼 표를 보기 전에 아래 문제를 염두에 두고 아래를 보거라.
|
둘째 방법은 앞에서 표로 본 것이야. 아주 오랫동안 세계 여러 곳에서 이 방법을 썼어. 셋째 방법은 큰 수부터 곱을 한 알고리듬. 그리고 마지막은 우리가 흔히 쓰는 방법. 그렇다면 첫째 방법은 어떻게 한 것일까?
첫째 방법을 어떻게 했는지 짐작해보겠니? 그리고 한발 더 나아가 문제 하나를 꼭 생각해 보기 바란다. 첫째 방법에는 흥미로운 사실이 숨어 있거든. 그것을 스스로 밝혀보는거야.
|
첫째 알고리듬으로 하면 항상 다른 방법과 같을까? 안되는 경우도 있지 않을까? 왜 그럴까? |
이 문제를 스스로 풀었다면, 어떤 묘한 즐거움이 함께 할 것 같아. 삼촌이 이렇다 저렇다 말로 설명할 수 없는 어떤 즐거움일거야. 이것에 대해서는 또 앞으로 다시 말할 때가 올거야. 하지만, 삼촌이 설명하기 전에 꼭 스스로 답해 보거라, 알았지?
오늘은 이 정도로 만족할까? 그리고 이제 무슨 이야기를 할까? 뺄셈과 나눗셈을 이야기할까? 덧셈과 곱셈을 한꺼번에 하는 경우를 볼까? 아니면 수가 아니라, 문자들이 쓰는 계산을 어떻게 하는지 볼까? 무엇이 좋을까? 점점 이야기를 풀어가는 길이 여러 갈래로 갈라지는구나. 어디로 갈까, 그건 다음 편지를 보면 알 수 있겠지? 안녕, 다음 편지까지 안녕 !

 수학 편지 대문으로.
수학 편지 대문으로.