Min Perimeter Triangle

삼각형의 가장 짧은 둘레

Q : 예각삼각형 ABC 이 주어졌다고 하자. 변마다 E, F, G 한 점씩 골라서 그 세 점이 이루는 삼각형의 둘레가 최소가 되도록 하려면 어떤 점을 골라야 할까?

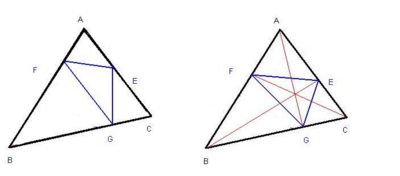
A : 주어진 삼각형 ABC 의 변마다 한점씩 골라서 삼각형을 이룰 때, 최소 둘레를 갖게 되는 삼각형은 주어진 삼각형 ABC 의 orthotriangle EFG 이다.

기초정리들

기초 정리 0 : 주어진 두 점 A, B 을 잇는 최단 거리를 이루는 것은 선분 AB 다.
기초정리 1 : 두 점 A, B 을 잡고 그 점이 이루는 직선 l 을 생각하자. 그 직선에 있지 않고 직선의 같은 방향 한 쪽에 두 점 U, V 을 정하자. 직선 위의 한 점 M 에서 두 점을 잇는 선분의 합 AM + MB 의 최단거리를 이루는 점 M 은 다음과 같은 성질을 갖는다.

\angle AMU=\angle BMV

기초정리 2 : 주어진 삼각형 ABC 의 한 꼭지점에서 맞은편 변에 수선들을 내려 orthotriangle EFG 을 냈다고 하자. 그럴 때 각 AFG 와 각 CFE 는 같다.

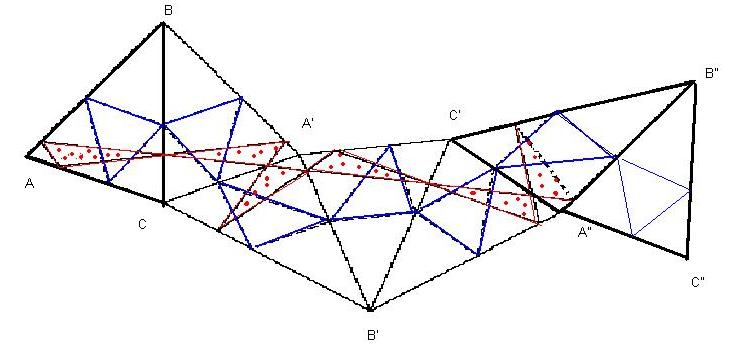
주어진 삼각형 ABC 가 있다고 하자. 이 삼각형의 한 변을 아무거나 정하자. 그 변이 BC 라 하면, BC 에 삼각형 ABC 를 선대칭한다. A 에 대칭인 새로운 꼭지점을 A' 라 하자.
이제 새로운 삼각형 A'BC 을 변 A'C 에 선대칭 이동한다. 새로운 점을 B' 라 하자.
새로운 삼각형 A'B'C 를 변 A'B'에 대해 선대칭 이동한다. 새로운 점을 C' 라 하자.
새로운 삼각형 A'B'C' 를 변 B'C' 에 대해 선대칭 이동한다. 새로운 점을 A" 라 하자.
새로운 삼각형 A"B'C' 를 변 A"C' 에 선대칭 이동한다. B' 에 대응하는 새로운 점을 B"라 하자.
이제 마지막으로 삼각형 A"B"C' 를 변 A"B" 에 대해 선대칭 이동한다. C' 에 대칭하는 점을 C" 라 하자.

처음 삼각형 ABC 의 변 AB, BC, CA 에 있는 점을 차례대로 G, E, F 라 하면, 그 점들도 마찬가지로 이동하여 마침내 G", E", F" 로 옮기게 된다. 다음의 사실을 주목하자.

BC 와 B"C" 는 평행이다.
선분 EE" 에는 선분 EF 와 같은 길이의 선분이 둘, GE 와 같은 길이의 선분이 둘, 그리고 선분 FG 와 같은 길이의 선분이 둘이다. 따라서 선분 EE"의 길이는 삼각형 EFG 의 둘레의 두배다.
이제 삼각형 ABC 의 변마다 아무 점이나 하나씩 U, V, W 잡아 삼각형 UVW 을 보자. 이 점들도 대칭이동하여 U"V"W" 가 될 것이다.
그럴 때, 점 U 와 U" 의 상응하는 변들을 잇는 '꺽인 선들' 의 길이의 합 UV'+ V'W + WU' + U'V" + V"W" + W"U" 는 삼각형 UVW 의 둘레의 두배다.
EE"U"U 는 평행사변형을 이룬다.

따라서, 삼각형 EFG 의 둘레의 길이는 그 점들이 아닌 점들로 이룬 삼각형 UVW 의 둘레보다 항상 작다. 따라서 삼각형 ABC 의 orthotrianlge 의 길이가 해가 된다.

쉬바르쯔의 해법은 그 증명에서 순수한 기하학적인 사고만을 썼고 기초적(elementary)이면서도 쉽고 단순하다는 점에서 놀랍다. 그렇다면 이 성질을 다르게 보일 수는 없을까? : 다른 해법 " 삼각형의 가장 짧은 둘레에 대한 다른 해법 : 어떤 방법이 더 있을까?
문제의 조건에서 '예각' 삼각형은 근본적으로 중요한 제한이다. 왜냐하면 그 해가 되는 삼각형은 orthotriangle 로서 삼각형의 변에서 한점씩 이루어 삼각형을 이루기 때문이다. 둔각이나 직각 삼각형은 그렇게 되지 않는다. 그렇다면 문제에서 나머지 조건은 그대로 두고 '예각' 대신 '직각'이나 '둔각' 삼각형이라면 어떻게 될까?
삼각형이 아니라 사각이나 오각, 육각, ... 과 같은 어떤 n 각형이 주어졌다고 할 때, 변마다 한점씩 잡아 새로운 n 각형을 이룰 때, 그 변의 길이가 최소가 되게 하려면 어떤 점들을 잡아야 할까? (이때도 쉬바르쯔가 증명에 썼던 아이디어가 쓸만할까?)