With Infinity Lines

무한과 사귀기 로

무한, 직선과 곡선

도형의 세계(기하;Geometry)에서 기본으로 여겨지는 듯하다. 도형의 가장 기본 단위를 점과 직선, 평면, 공간으로 여긴다. 여기서 점을 빼고는 어떤 것도 모두 무한적인 것들이다. 직선부터 두 점을 잇는 '무한'한 점들을 생각할 수 밖에 없다. 하지만, 워낙 기초적인 것이라 더 천천히 따져봐야할 것들이 있다.

직선과 곡선

무엇이 직선이고 무엇이 곡선일까? 흔히 직선하면 반듯한 자로, 흐트러짐없이 그리는 것을 떠올린다. 이 자체를 잘못이라고 할 수는 없다. 하지만, 꼭 그렇게만 되어야 하는 것일까? 직선이 '완벽하게 반듯한' 것이라 한다면, 세상에 있는 어떤 자로도, 사실, 정확한 직선을 그릴 수는 없다. 우리가 직선을 그리는 데 쓰는 자나 연필, 종이는 제아무리 잘 만든다고 해도 완벽할 수는 없기 때문이다. 컴퓨터에 그린 직선도 마찬가지다. 어떤 도구를 쓰든 우리가 그린 것을 점점 확대해간다고 해보자. 돋보기를 다섯배, 백배, 천배 키우면서 보면 볼수록 직선은 휘어있고, 게다가 면적을 갖고 있는것을 발견할 수 있다. 그렇듯 눈으로 볼 수 있는 유한의 세계에서는 완벽한 도형이 존재하지 않는다. 다만 무한을 상상할 수 있는 우리의 이성의 눈만이 그것을 볼 수 있을 뿐이고 그래서 그런 도형이 있다는 것을 믿게 된다.

원과 다각형은 무엇이 다를까?

아래 그림을 보자. 아래 그림은 볼록정다각형들을 겹겹이 쌓아놓은 것이다. 정 3각형, 정4각형, 정5각형, ... 정17각형, 정 19각형, 가장 마지막 테두리에 정 20각형까지 그려져 있다.

Q. 1각형, 2 각형이 있을까?

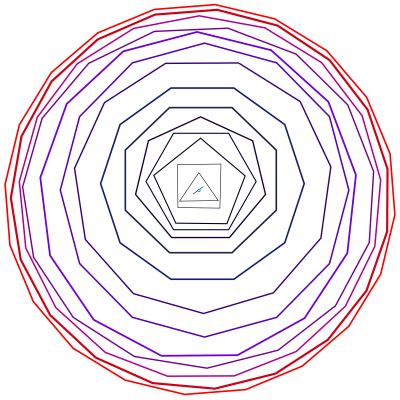
보다시피 정 20각형만 해도 원과 매우 흡사하다. 정 100각형을 상상해보자. 정 100각형을 공책에 그려서 누군가에게 이것이 어떤 도형일까? 물으면 대부분의 사람들이 "그거야 원이지!" 하고 답할 것이다. 하지만 정n각형에서 n이 아무리커도, 다시 말해

정 $9^{9^{9}}$ 각형

이라 하더라도, 그 n 이 유한이라면, 원이 될 수 없다. 원은 주어진 중심에서 어떤 점이나 상관없이 같은 거리에 있을 것이기 때문이다. 그래서 꼭지점 마다 순서대로 1, 2, 3, ... 과 같이 번호를 붙인다면,

$9^{9^{9}}-1$ 번 꼭지점과 $9^{9^{9}}$ 번 꼭지점 사이의 점들

은 중심에서 다른 거리에 있게 될 수 밖에 없다.

Q. 왜 그럴까? 스스로 답을 해보아라.

따라서 어떤 정n 각형의 둘레를 구해도 그것은 원의 둘레와 같아질 수 없다. 그래서 원의 둘레를 나타낼 때, 정확히 알 수 없는 어떤 수 $\pi$ 로 나타내게 된다.

원과 같아지려면 n 이 유한의 한계를 넘어서야만 한다. 수천년 전 사람들도 이와 비슷한 생각을 하였다. 원의 둘레나 면적을 구하기 위한 생각으로 원에 꼭지점을 대면서 '원 안'에 정다각형을 그리면서 꼭지점의 수를 점점 늘려가보았다. 하지만, 그때는 계산 기술이 지금 여러분과 비교해도 턱도 없이 부족했기 때문에 정다각형을 몇 개도 채 그리지 못했다. 세월이 한참 흐른 뒤에야 '원 밖'에도 그와 비슷한 시도를 해서 이것들 사이의 값이 원이어야 한다는 사실을 알았다.그 사람이 고대 그리스 최대의 수학자인 아르키메데스다. 아르키메데스는 원의 안과 밖에 정 6각형부터 96각형까지 계산한 다음 원의 둘레의 근사값을 얻었다. 그래서 $\pi$ 라를 수가 놓인 범위를 알수 있게 되었다. 지금 언어로 쓰면,

$3{\frac {10}{71}}<\pi <3{\frac {10}{70}}$

이다.

여기까지 깊이 들어갈 수 없지만, 질문이라도 하고 넘어가지 않을 수 없는 문제 둘을 추가하고 다음 주제로 넘어가기로 하자.

하나는 작도와 연관된 문제다. 작도는 자와 컴퍼스만 쓰는 것으로 제한한다. 이 문제는 처음 이 문제를 던진 후 수천년이 흘러서야 완전한 답을 찾을 수 있었다. 이 문제를 해결하는데는 열아홉살 가우스 가 해낸 정 17각형 작도 가능의 증명이 중요한 역할을 했다. 그 증명에서는 뜻하지 않게 허수 i 가 핵심적인 역할을 한다. 작도라는 도형의 문제가 수의 세계에서 풀린 것이다 !

Q. 정 3각형에서 정 20각형 중 어떤 것들을 자와 컴퍼스만 써서 작도할 수 있을까?

2차원인 평면에서는 특수한 경우를 생각하지 않는다면 최소한 직선 셋이 있어야 다각형(삼각형)을 이룰 수 있다. 넷, 다섯, .. 직선이 많아지면 많아질수록 다각형의 종류는 더 풍부해질 것이다. 이런 사정은 공간에서도 마찬가지다. 3차원 공간에서는 최소한 네 2차원 평면이 있어야 어떤 닫힌 4면체를 이룰 수 있다. 그런데, 과연 평면에서 가능했던 것이 공간에서도 통할까? 평면에서는 어떤 자연수에 대해서도 (정 1,2 각형도 있다면) 정다각형이 있다. 공간에서도 가능할까?

Q. 공간에서 정다면체도 정 4 면체, 정 5 면체, 정 6 면체, 정 7 면체, 정 8 면체, 정 9 면체, ... 같은 것이 있을 수 있을까?

직선과 곡선은 무엇이 다를까?

수천년 동안 도형의 성질을 탐구해 오면서 사람들은 도형 자체를 보아왔다. 원, 삼각형, 사각형 처럼 비교적 쉬워 보이는, 자와 컴퍼스로 작도할 수 있는 것에서 부터, 원추를 잘라내며 만들어지는 도형들 ( 타원, 쌍곡선, 포물선 ) 그리고 더 이상해보지만, 규칙을 분명히 알 수 있는 도형들, 회오리, Quadratrix, Conchoid 같은 도형들을 본 것이다. (옆에 그림 참고)

Conchoid

Archimedes Spiral

Fermat Spiral

Quaratrix

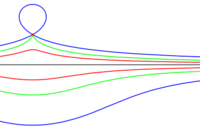
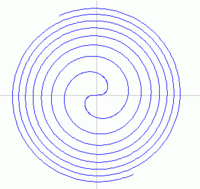
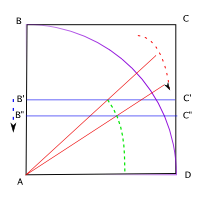
그런데, 이런 상황은 17세기 수학의 중심이 지금의 유럽으로 옮겨 오면서 달라진다. 특히 페르마와 데카르트의 생각이 담긴 좌표법은 그동안 도형의 세계와 수의 세계를 떼어놓고 보던 사고의 틀을 깼다. 물론 여기에는 함수(function)라는 개념이 발전하고, 수와 식을 쓰는 방식을 넓히고 기호를 쉽게 쓸게 있게 해준 그 이전의 중심, 인도 아랍 수학의 발전 덕분이다. 이제 우리는. 예를들어,

$y=x^{2}$

라는 식이 성립하는 (x, y) 수의 쌍을 평면에 '찍어서' 볼 수 있게 되었다. 또는 그 반대로 아래 그림처럼 그려진 도형을 식으로 가져갈 수 있게 되었다. 그런데 원에서 그랬던 것처럼 우리가 아무리 정확히 이 그림을 그리려고 해도 매우 근사적으로 가까이 그릴 수 있을 뿐, 완벽하게 그릴 수는 없다. 앞의 식에서 만약 x 에

$1,\ 1.5,\ 2,\ 2.5,\ 3,...$

같이 수가 있다면 그에 대응하는 y 는

$1^{2},\ 1.5^{2},\ 2^{2},\ 2.5^{2},\ 3^{2},...$

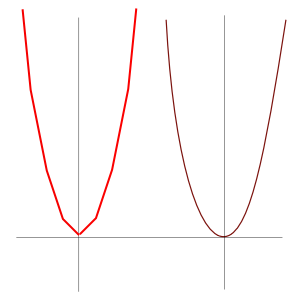
이 될 것이다. 이점들을 이으면, 아래 왼쪽 그림처럼 '꺽여지는 직선'들이다. 여기서 x 의 후보들의 간격을 0.5로 했기 때문에 이것을 더 촘촘하게 한다고 하자. 0.1로 한다면,

$1,\ 1.1,\ 1.2,\ 1.3,\ 1.4,\ 1.5,...$

가 될 것이고 그때 대응하는 점은 수의 쌍으로

$(1,\ 1.1^{2}),\ (1.1,\ 1.1^{2}),\ (1.2,\ 1.2^{2}),\ (1.3,\ 1.3^{2}),\ (1.4,\ 1.4^{2}),\ (1.5,\ 1.5^{2}),...$

와 같이 될테지만 역시 그 점들을 이어도, 마찬가지로 꺽인 직선들일 뿐이다. 간격을 0.01, 0.001 , ... 로 좁혀가도 마찬가지다. 원에서처럼 매우 근사적으로 곡선을 그릴 수 있을지언정, 좁히는 간격이 유한하다면 결국 우리는 곡선을 얻을 수 없다. 그렇다면 도대체 곡선이란 무엇일까? 앞의 이야기를 연장해서보면, 좁히는 간격을 '무한하게' 좁힐때 비로소 곡선을 얻게 된다는 말이 된다.

직선과 곡선의 차이를 다르게 설명할 수도 있다. 결국 같은 이야기가 되고 말지만. 다르게 한번 시도해보겠다. 우리의 생각과 맞는 곡선이라면 이런 일이 벌어지고 말 것이다. 먼저 상상을 해보자. 곡선의 어떤 한 점을 잡는다. 그리고 그 곡선의 다른 점에도 하나 찍는다. 두 점을 이으면 이 곡선을 교차하는 직선이다. 그 두 점의 기울기를 찾을 수 있다. 그리고 두 점의 '사이에' 있는 두 점을 잡고 기울기를 얻는다. 다시 그 두 점의 사이에 있는 또다른 두 점을 잡고,... 이런 식으로 계속, '끝없이' 좁혀들어간다고 해보자. 이 곡선이 끊어진 게 아니라면 결국 두 점은 한 점으로 다가 갈 수 밖에 없다. 그 점을 (x, y) 라고 써보자. 이것은 우리가 무리수를 볼때 했던 것과 같은 생각이다. 이제 이 기울기들만을 보자. 그러면 그 값들도 점점 어떤 값으로 다가가게 된다. 끝없이 이 과정을 해갈 때 이 '다가간 값'을 우리는 그 점 (x,y) 에서의 기울기라고 한다. 그림을 대강 보면 이렇다.

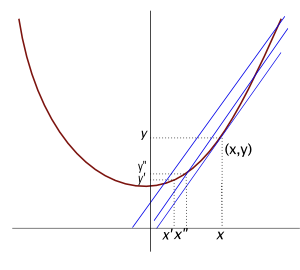
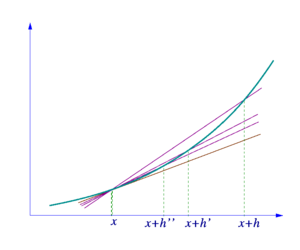
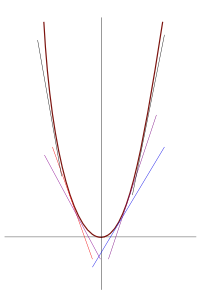
그렇다면 이제 곡선을 말할 수 있는 다른 표현을 얻은 셈이다. 어떤 점에서의 기울기로 표현할 수 있는 것이다. 그런데 점의 기울기는 지금까지 여러차례 나온 '끝없이 어떤 하나로 다가감' 이라는 생각을 적용한 것이다. 곡선이라면 어떻겠는가? 그렇다고 곡선이라면 어떤 점 근방에서의 기울기가 다를 수 밖에 없는 바로 그런 선이다. 직선은 ? 물론 그렇지 않고, 어떤 근방에서 기울기가 같은 선을 뜻한다.

한 직선과 만나지 않는 무한개의 직선

"수학의 시작" 을 언제라고 볼 수 있을까? 그 질문 자체가 잘 만들어진 게 아니라, '수학'과 '시작'에 대해 달리 생각하는 사람마다 답이 다를 수 있다. 하지만, 어떤 답을 내든 정답을 찾기 위해 고려하지 않을 수 없는 중대한 사건이 있으니, 2500여년 전 고대 그리스 영토이자 당시 학문의 중심지였던 알렉산드리아에서의 일이다. 유클리드라는 학자가 쓴 입문 이라는 책이다. 이 책은 그때까지 수학을 집대성하여 의심할 여지 없는 단순한 사실들 몇가지로부터 엄격하게 증명해가는 방식으로 썼다. 이 '의심할 수 없는 몇가지' 중에 그후 이 천여년 동안 사람들이 줄곧 의심해온 사실이 하나 있다. 바로 유명한 '평행선 공리'다. 그 사실은 이렇게 표현된다.

한 평면에 어떤 하나의 직선이 있을 때, 그 직선에 있지 않은 한 점을 지나면서 그 직선을 지나지 않은 직선은 하나 뿐이다.

그림으로보면 아래와 같다.

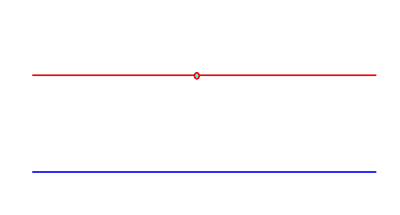
이것을 당연하다고 받아들이는 사람들이 있었고, 그렇지 않은 사람들이 있었다. 당연하다고 받아들이지 않은 사람들은 이것은 다른 '의심할 수 없는 사실' 들로부터 증명할 수 있다고 생각하는 사람들이었다. 이것을 증명하기 위해 수많은 시도들이 있었고 실제로 증명한 사람들이 여럿있었다. 하지만, 그것을 증명한 사람들이 '의심할 수 없다'고 믿었던 사실은 평행선 공리로 증명할 수 있었다. 그래서 이 두 사실은 말은 다르지만 논리적으로 같은 것이나 진배없는 게 되버린다. 그렇다면 왜 사람들은 이것을 더이상 의심할 수 없는 사실로 받아들이지 않았을까? 이것을 설명해갈 길을 여럿이지만, 그 중 무한과 관련해서 이야기해보기로 한다. 그 전에 이 사실부터 밝혀보라.

Q. 한 평면에 어떤 하나의 직선이 있을 때, 그 직선에 있지 않은 한 점을 지나면서 그 직선을 지나지 않은 직선은 있다.

최소한 하나 있는 것은 분명하다. 그리고 그것을 작도할 수 있고 따라서 증명할 수 있다. 그런데 하나뿐이어야 하나? 그 직선이 오직 하나뿐 이라는 사실은 의심할 수 없이 받아들여야 할까? 아래 그림을 보자.

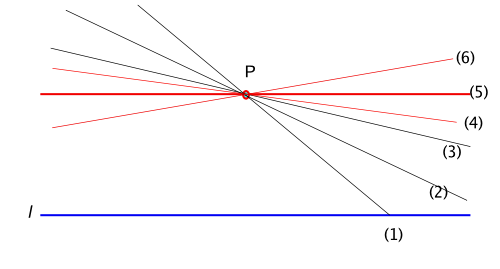
그림에서 주어진 직선은 l 로 그 직선에 있지 않은 점은 P 로 표시했다. 이제 P 를 지나는 직선 (1)을 그어보자. 직선 (1) 은 직선 l 과 한 점에서 만난다. 이제 점 P 에서 그 직선 (1) 보다 각을 '좁혀서' 직선을 그어보자. 직선 (2) 도 어디선가 만난다. 하지만, 직선 (1) 과 l 이 만난 점에서부터 '멀리' 떨어진 점일 것이다. 다시 각을 더 좁혀보자. 직선 (3) 도 직선 l 과 만날 수 있다. 어디선가. 하지만, 이 점은 아주 아주 멀리 떨어진 점일 것이다. 이제부터는 각을 아주 조금 좁혀도 만나는 점은 엄청나게 멀어진다. 마치 우리가 수에서 몇제곱에 몇제곱을 한 것처럼 각을 조금만 좁혀도 멀어지는 정도는 엄청나게 커질 것이다. 각을 극도로 작게 할 수록 만난 점은 점점 멀어져서 '무한'에 가까운 어떤 데로 갈 것이다. 그렇다면 어디서부터는 직선 l 과 최초로 만나지 않는 직선이 있을 것이다. 이 직선을 (4)라고 해보자. 이제 점 P 에서 점점 더 작게 회전하다가 보면, 결국 직선의 반대쪽에서 연장한 직선이 만나게 된다. 직선(6)이 바로 그런 직선이다. 이 사이 어딘가에 우리가 평행하다고 여겼던 유일한 직선 (5) 가 있다. 그렇다면 직선 (4)부터 직선 (6) 사이에 있는 모든 직선은 다 직선 l 과 만나지 않는다. 왜 l 과 만나지 않은 직선이 꼭 하나만 있어야 한단 말인가?

평행선은 절대 안만날까 ?

지금까지 본 것만으로해도 무한의 세계는 끝이 없다. 새로운 상상을 하나 더 해보자. 평면이 있고, 공모양의 입체 도형이 하나 있다. 평면과 직각을 이루면서 공을 '끝점'을 지나는 두 점 중 밑에 있는 것을 남극, 위쪽에 있는 것을 북극이라 한다. 이것을 S, N 으로 아래 그림에서 표시했다.

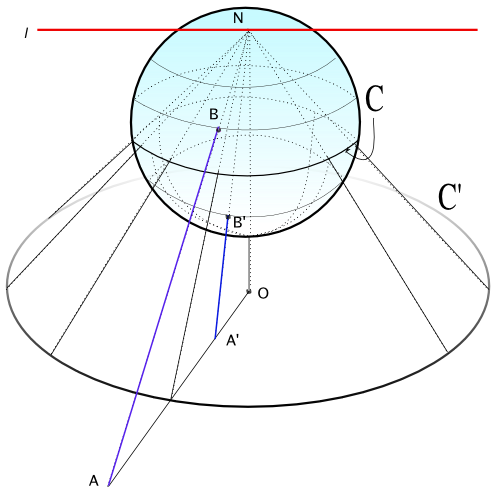
이제 점 N 에서 빛을 쏜다고 해보자. 이 빛은 직선으로 간다고 가정한다. 그래서 북극점 N 에서 직선빛을 쏴서 그 직선이 공의 점들 A 와 어떤 평면 A' 와 만날 것이다. 거의 대부분의 점에서는 이렇게 된다. 뿐만아니라 공의 표면에 있는 '거의 모든 점'과 평면의 '모든' 점이 하나씩 대응한다. 공의 한 점이 평면의 두 점으로 대응할 수 없다. 빛을 남극점 S 에 쏘면 평면과 직각으로 내린 점 O 가 대응하는 점이다. A 에 쏘면 A', B 에 쏘면 B' 들이 대응한다. 그러면 북극점 N 에 매우 가까이 있는 점들은 어떻게 될까? 그렇다. 점점 점 O 로 부터 멀리 떨어지게 된다. 북극점 N 에 가까이 오면 올수록, 무한히 가까이 오면 올수록 평면에 대응하는 점들은 무한히 멀어진다. 그렇다면 여기서 질문.

Q. 점 N 자신은 어디로 대응할까?

또 다른 상상을 해볼 수도 있다. 이번에는 공이 떠 있는게 아니고, 어떤 평면이 떠 있고 하자. 평면 P 가 있고, $P_{1}$ 가 떠 있다. 두 평면에 있지 않은 다른 곳에서 빛이 나온다고 해보자. 그 점을 O 라 한다. 이 점에서 직선빛을 쏴서 평면 $P_{1}$ 에서 A 를 지나고 평면 P 에서 A'로 지난다면 이때도 두 평면의 점들은 하나씩 대응한다. 이제 평면 $P_{1}$ 을 점점 평면 P 에 직각이 되게 기울여가보자. 어떤 일이 일어나는가 아래 그림을 보고 미루어 짐작해보라.

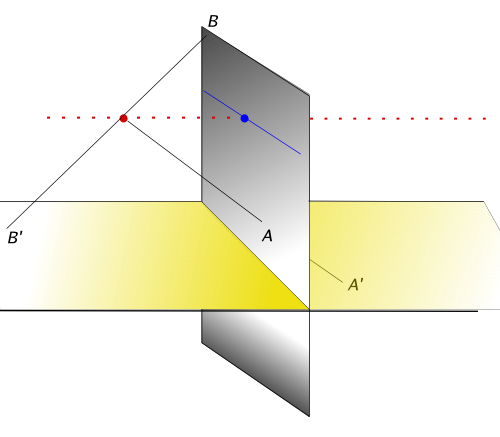
Note

Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia