Prime Distribution: 두 판 사이의 차이
(차이 없음)
|
2008년 12월 31일 (수) 12:28 기준 최신판
어떻게 소수를 찾아낼까?
소수를 어떻게 찾을까? 자연수 1, 2, 3, ... 을 넣어서 소수 만을 차례로 늘어놓는 단순한 규칙이 있으면 더 없이 좋겠지만 소수가 '내가 생긴 모습은 바로 이러하오' 하고 순순히 그 구조를 드러내지 않을 것 같다. 그렇다고해서 소수의 구조를 알아내려는 탐구자들의 발길은 끝나지 않고 있다. 그 중
- 어떤 자연수 N 보다 작은 소수들 전부를 찾는 방법들은 생각해 볼 수 있지 않을까?
- 소수 전부를 찾는 규칙은 아니라도 소수만 끝없이 많이 생성할 수 있는 알고리듬은 없는 것일까?
- 단순하지 않더라도, 모든 소수를 만들어내는 알고리듬(대수적 식)은 과연 없는 것일까?
- 어떤 자연수가 주어지면 그것이 소수인지 아닌지 금방 알아낼 방법이 없을까?
- 어떤 구간 안에 소수는 고루 퍼져 있을까?
하는 물음표들이 소수 탐구로의 여정에 저마다의 길을 내고 있다.
지금 이 순간에도 지구촌 어디선가는 이에 골몰하고 있는 사람들이 꽤 될 것이다.
소수 거르기
에라토스테네스의 체로 거르기
어떤 자연수 N 까지 있는 소수들을 골라내는 방법 중 가장 오래된 것은 '에라토스테네스의 체(Eratosthenes' sieve)'일 것이다. 이것은 자연수들을 놓고 흔들어서 후두둑 떨어뜨리고 남은 것만 체로 거르듯 하는 방법이다.
- (에라토스테네스의 체 방법) 처음 발견된 소수 2에 동그라미치고, 그것의 두 배, 세 배, 네 배 ... 되는 수들(2의 배수)를 모두 지운다. 남은 수 중 2 다음 수 3 에 동그라미하고 나서 3 의 배수를 다 지운다. 이런 식으로 N 까지 모든 자연수에 표시가 될 때 까지 반복한다.[1]
알고리듬이 무척 단순하다. 실제로 주어진 수 N 이 작을 때 아주 빠른 방법이다. 그렇지만 N이 커질수록 효율성은 급속히 떨어진다.
아트킨의 체로 거르기
체 거르는 방법이 꼭 이 방법만 있을리는 없다. 자연수와 소수의 성질을 잘 파악해서 다른 체를 고안해볼 수 있다. 그 중 현재까지 알려진 것 중 가장 중요한 것으로 여겨지는 체가 있다. 에라스토테네스 처럼 '거르는' 행동을 반복하는 알고리듬인데, 아트킨(A. O. L. Atkin)[2] 과 번쉬타인(D.J.Bernstein;1971~) [3]이 2004년 발표해서 아트킨(Atkin)의 체라고 불린다.
- N 까지 자연수들로 된 모든 가능한 (x,y)를 를 고려하게 된다. 다시 말해 { (x,y) | x [1,N], y [1,N] }
- 인 수가 4 로 나눠 1 인지 본다. 만약 그렇다면 체 안에 남기고 나머지는 다 버린다.
- 인 수가 6 으로 나눠 1인지 본다. 만약 그렇다면 체 안에 남기고 나머지는 다 버린다.
- 인 수가 x > y 이고 12 로 나눠 11 인지 본다. 만약 그렇다면 체 안에 남기고 나머지는 다 버린다.
- 남은 n 들 중에서 곱셈이 두 번 들어간 수는 버린다.
마지막 단계에서 '제복이 두 번 들어간 수란, 예를들어 27 같은 수다. 3*3*3 니까 3의 제곱꼴이 들어있다. 그에 비해 35 같은 수는 5*7로 제곱이 안들어간 형태다. 제곱이 두 번 들어간 수를 골라내는 것은 그리 어렵지 않다. 주어진 N 보다 작은 수 중 {n^{2}, 2n^{2}, 3n^{2}, ...} 을 만든 다음 이것들과 비교해서 이 안에 들어있으면 그것은 버리면 충분하다.
그러니까, 에라스토테네스 체는 처음엔 2 로 거르는 체, 다음엔 3 으로 거르는 체, 그 다음엔 5 로 거르는 체, ... 와 같이 수가 커질수록 새로운 체를 써서 거르는데 비해, 아트킨의 체는 3(또는 4 개)의 체로 거른다. 위의 알고리듬이 가능했던 것은 소수에 대한 통찰력에서 비롯된다. 다음의 세 정리가 기초가 된다.[4]이해가 편하게 자연수에 대해서만 보면,
- n 이 4k+1 꼴이고 제곱이 들어가지 않은 수라 할 때, n 이 소수 이 홀수.
- n 이 6k+1 꼴이고 제곱이 들어가지 않은 수라 할 때, n 이 소수 이 홀수.
- n 이 12+11 꼴의 제곱이 들어가지 않은 수라 할 때, n 이 소수 이고 이 홀수.
어떤 주어진 수가 소수일 필요충분조건을 파악하여 알고그림으로 반영한 결과, 아트킨 체는 지금까지 알려진 방법 중 결과를 빨리내고 메모리를 적게 차지하는 기준으로 비추어볼 때 최상급 알고리듬으로 여겨진다.
소수를 만들어내는 식
소수 전체만을 나타낼 수 있는 단순한 규칙은 아직 밝혀지지 않았다. 그것을 알아내면 자연수의 가장 기초적 구성 원소들이라 할 수 있는 소수의 구조를 완벽하게 파악해냈다는 뜻이다. 고대 그리스의 현자들 이래 '수학적 직관력'으로 그것은 난해한 문제로 받아들여졌다. 하지만, 거기는 마침표가 아니라 물음표가 찍히는 지점이다. 소수 전부는 아니더라도 "소수만 계속 만들어낼 수 있는 간단한 규칙조차 없는 것일까? " 이 미개척지로 길을 낸 첫 모험가는 페르마였다.
페르마의 가설
이미 소수의 무한성에 대한 페르마의 증명 부분에서 간단히 언급했다. 요점만 옮긴다.
- 페르마가 제안한 '소수만을 만들어내는 함수'라고 제안한 함수는 아래와 같다.
이 수가 얼마나 빨리 커지는가?
- f(1) = 5, f(2) = 17, f(3) = 257, f(4) = 65537, f(5)= 4294967297
이다. n이 4일 때는 다섯자리수이다가 n이 5일 때 열 자리수가 되었다.
- f(1), f(2), f(3), f(4) 는 모두 소수지만, f(5) 는 소수가 아니다. (오일러)
- n 이 4 보다 클 때, f(n)이 소수가 있는지 없는지 아직 밝혀지지 않았다.
특정한 수까지 계속 소수를 만들어내는 함수
페르마가 시도했던 것은 자연수가 1, 2 , 3, 4 까지만 소수가 나오고 5에서는 소수가 아니었다. 그리고 그 이후는 '대부분 또는 모두' 소수가 아니다. 이에 비해 0, 1, 2, 3, ... 부터 어느 정도까지는 소수만 만들어내는 다른 규칙들이 있다. (예 1 )
| 3! - 2! + 1! | = | 5 |
| 4! - 3! + 2! - 1! | = | 19 |
| 5! - 4! + 3! - 2! + 1! | = | 101 |
| 6! - 5! + 4! - 3! + 2! - 1! | = | 619 |
| 7! - 6! + 5! - 4! + 3! - 2! + 1! | = | 4421 |
| 8! - 7! + 6! - 5! + 4! - 3! + 2! - 1! | = | 35,899 |
| 여기까지는 소수들이지만, | ||
| 9! - 8! + 7! - 6! + 5! - 4! + 3! - 2! + 1! | = | 326,981 = 79*4139 |
더 단순한 예가 있다.
- (예2)
이 예에서 n 에 1, 2, 3 ... 을 차례로 넣은 결과 f(0), f(1), f(3)...은 모두 소수다. 단 40 까지. 41을 넣으면 제곱수 이므로 소수가 아니다.
- (예3)
이 예는 은 n이 0 부터 79까지일 때 모두 소수를 만들어낸다.80을 넣으면 소수가 아니다.
모든 소수를 만들어내는 식
과연 모든 소수를 만들어내는 식은 불가능할까 ? 불가능하지는 않다. 결국 찾아내기는 찾아내었다. 그러나 그 식은 대단히 복잡한 식으로 드러나 실질적으로 '소수의 구조'를 파악하는데든 결정적 단서를 주지 않았다. 그 역사 속으로 잠시 들어가보자.
1900년 세계 수학자 회의에서 힐버트는 20세기 안에 풀어야한 가장 중요하다고 느끼는 Hilbert의 20세기의 수학문제 23 개를 제안하였다. 그 중 10번째 문제를 풀어 말해보면
- 모든 디오판테스 방정식은 해를 가지거나 가지지 않는다고 결정할 수 있는가?
였다. 해를 가지는지 아닌지 풀어낼 일반적 알고리듬이 과연 있는가 하는 문제였다. [5]이전 연구자들의 성과를 바탕으로 1970년 러시아의 수학자 마티야세비치가 완결적인 답을 냈다. '그런 알고리듬은 없다' 로 드러났다. 그렇다면 구체적으로 어떤 디오판테스 방정식이 해를 갖지 않는다는 말인가? 그로부터 몇 년 뒤, 그런 알고리듬이 존재하지 않은 예가 나타났다.(J.James) 방정식 묶음(system of equations ; 연립방정식) 인데, 그 묶음은 차수, 33개 변수를 가진 18개의 방정식으로 이루어져 있다. 그런데 뜻밖에도 이 '부정적' 결과로부터 소수 만드는 알고리듬과 관련하여 '긍정적' 결론이 유도되었다.
- 변수에 양의 정수값을 넣으면 소수 모두를 만들어내는 23개 변수를 가진 다항식이 존재한다.[6]
하지만 이 다항식은 지나치게 복잡했다. 그 이후 상대적으로 그 보다는 다항식이 제안되었는데 이 다항식은 26개의 변수로 되어 있다.[7]더 단순해졌다고는 하지만 이 다항식은 여전히 만만하지 않다. 소수의 구조에 대해 결정적인 단서를 주지 않는다. 이 다항식의 의미는 '어떤 다항식'이라는 알고리듬으로 소수가 생성되므로 소수가 '셀 수 있는 집합[8]'이라는 구체적인 정보 말고는 특별한 것이 없다. [9]
등차수열에 있는 소수들
모든 자연수에 대하여 소수가 무한개라는 것은 이미 보았다. 그렇다면 자연스럽게 다른 질문이 이어질 수 있다. 모든 자연수가 아니라 어떤 성질을 갖는 무한 개의 자연수들만 뽑아보면 그 안에도 소수가 끝없이 많을까? 이 물음은 소수가 어디서 밀집되어 있고 어디서 띄엄띄엄있는지 하는 물음과도 맞닿아있다. 그 중 먼저 확인해볼만한 물음은 이런 것이다. : 일정한 간격으로 '고르게' 떨어진 자연수들만 보면 그 안에 소수가 끝없이 많이 있을까 ? 어떤 수 부터 시작해서 일정한 간격으로 떨어진 수들의 열을 등차수열(앞 수나 뒷 수와 차이가 같은 수들의 열) 이라 한다. 시작하는 수를 초항, 간격을 등차라고 부르기도 한다.
예를 보면서 생각해보자.
- 3n + 2 꼴인 소수는 끝없이 많을까?
- 4 n + 3 꼴. 이 수는 는 7로 시작해서 4씩 끝없이 커져가는 자연수들 3, 7, 11, 15, 19, 23 , ... 이다. 이 안에는 소수가 끝없이 많이 있을까?
- 5 n + 4 꼴. 이 수는 4, 9, 14, 19, 24, 29, ... 이다. 이 안에는 소수가 끝없이 많이 있을까?
- 6 n + 3 꼴. 이 수는 3, 11, 17, 23, 29, 35, ... 이다. 이 안에는 소수가 끝없이 많이 있을까?
이 꼴을 갖는 소수는 끝없이 많다는 것을 보이는 것은 큰 수고를 들이지 않아도 된다. (스스로 해보라.) 이를 더 일반적으로 나타내면, n =1, 2, 3, ... 일 때,
- d n + (d - 1) 꼴인데 이런 꼴의 소수는 항상 끝없이 많다.
그렇다면,
- d n + 1 꼴의 소수도 끝없이 많을까?
예를들어, 4 n + 1 꼴의 수는 1, 5, 13, 17, 21, 25, 29, 33, 37, ... 인데 이 안에도 소수는 끝없이 많을까?
언뜻보기엔 위의 질문이나 이 질문이나 다를 것이 없어보인다. 그것을 증명하는 어려움의 정도도 비슷할 것 같다. 뜻밖에도 이것을 증명하는 것은 위의 3n + 2, 5n + 3 꼴을 증명하는 수준을 훨씬 넘어선다. 실제로 4 n + 1 꼴의 수와 4 n + 3 꼴의 수는 겉으로 봐서는 별로 다를 바 없어보이지만, 한꺼질 벗기고 보면 묘하게 다른 성질을 가지곤 한다. 예를 들어 4 n + 1 꼴을 갖는 소수들을 보면, 5, 13, 17, 29, 37, .... 인데, 이 수들은 모두 피타고라스 세쌍수의 빗변에 해당하는 수이다. 이런 성질에 대해서는 따로 보기로 한다. [10] (이에 대해서 '소수의 분포'에 관한 증명 모음 참고.)
위에 보인 수의 열을 일반화하면 물음표를 던지자. d n + a 꼴이다. n 은 1, 2, 3, ... 이라고 하자. 그렇다면
- 과연 d n + a 꼴의 소수는 끝없이 많을까? d 와 a 가 어떤 관계일 때는 끝없이 많고 어떤 관계일 때 끝이 날까?
수학이라는 우주가 던진 질문에 대해 19세기 수학의 거장 디리흘레 는 다음과 같이 답했다.
- (디리흘레 정리) n > 0 일때, 서로 소 관계인 a 와 d에 대하여 d n + a 꼴의 수들에는 a 와 d 에 상관없이 소수가 끊없이 많다.
수학의 기나긴 역사에서 기념비적인 작품이다. 이 증명에는 함수론과 해석학에 대한 고난도의 기법들이 씌여 몹시 난해하다 한다. 그리고 아직까지 충분히 쉬운 증명은 발견되지 않았다. (우리가 언젠가 여기까지 가볼 수 있기를!)
- 다음 질문에 답해보라.
- 3000보다 작은 열 개의 소수가 등차수열을 이룬다. 이 소수 열 개를 찾아보아라.
- 20000보다 작은 자연수 안에는 등차수열을 이루는 11개의 소수가 있을 수 없다.
소수 분포에 대한 정리
아직까지 소수의 구조는 매우 복잡하고 신비롭다. 언뜻보면 소수들은 온통 불규칙하게 나타나는 것처럼 보인다. 소수가 자연수 전체에 얼마나 띄엄띄엄 있을까? 어디는 우르르 몰려 있고 한동안 텅비어 있는 구간이 있을까? 아니면 어느정도 떨어져서 보면 분포가 마냥 불규칙한 것은 아니고 '어느 정도'의 규칙성은 있는 것일까?
소수가 없는 구간은 얼마나 넓을 수 있을까?
어떤 소수와 그 다음 소수는 수가 커질수록 점점 벌어진다. 이것은 '에라토스테네스 체'와 같은 방식을 생각해보면, 우리의 직관과 크게 다르지않다. 하지만 정말 그런 것일까?
- 소수아닌 수의 구간은 얼마든지 넓어질 수 있다.
어떻게 보일까? 소수의 처음 부분을 보면 촘촘하다. 그러다가 점점 띄엄띄엄 나타난다. 소수의 정의 부분에 나온 최초 100 개의 소수를 관찰해보라. 그런데 다음의 수들을 잘 보자.
- 7 은 소수다. 그 다음에는 8, 9, 10 이 있다. 다시 말해 다. 를 할 때 드디어 소수가 나온다. 그보다 넓은 구간을 보이는 것도 마찬가지 방법이다.
- 까지 모두 합성수고 마침내 일 때 소수다.
- 는 합성수고 은 소수.
- 10 개의 합성수 구간을 잡으려면 어떤 적당한 정도의 소수들의 곱인 N 에 2 를 더하고, 3 을 더하고 12 까지 더한 다음 12 까지 더했을 때 합성수가 나오고, 13 을 더하면 소수가 나오도록 하면 된다. 그런 N 은 일 것이다.
자 그렇다면 다음을 풀어보라.
- 백 개, 천 개, 만 개의 합성수가 연속해서 나오고 이어서 소수가 나오도록 할 수 있는 방법은 ?[11]
어떤 구간 안에 항상 소수는 있을까?
이런 질문을 해볼 수 있다. '충분히 넓은 구간을 잡았을 때, 그 안에는 항상 소수가 있을까?' 예를 들어 n 이 2 보다 크다고 할 때,
- n 과 n! 사이에는 항상 소수가 있을까 ?
n! 은 n (n-1) (n-2) 321 을 뜻하는 함수다. 다른 구간도 생각해보라.
아니면 이런 물음은 어떤가?
- 자연수 n을 정했을 때, 그 안에 있는 소수의 개수는 n 과 어떤 관계일까?
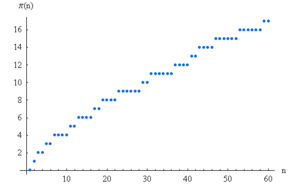

앞에서 어떤 수 n 까지 소수를 찾는 알고리듬에 대해서 에라토스테네스 체와 아트킨 체를 보았다. 그 알고리듬만 있는 것이 아니다. 앞으로 더 좋은 알고리듬들이 있을 수 있다. 어쨌든, n 까지 소수의 개수를 찾을 수 있는 도구가 우리에게는 있다. 그것은, 어떤 자연수 n 을 넣으면 함수의 개수 m 을 나타내는 함수다. 이를 로 쓰자. 에라토스테네스 체를 비롯한 '경험적인 방법'으로도 결과값은 알 수 있다. 예를들어,
이다. 그런데 그 때의 의 일반식은 어떻게 될까? 다시 말해 자연수와 소수의 개수를 연결하는 함수는 과연 어떤 꼴로 나타날까?
이 함수를 찾기 위해 수많은 노력이 있었지만, 소수의 세계는 그리 쉽게 비밀의 정원으로 가는 길을 보여주지 않았다. 함수 는 그 정확한 모습을 좀처럼 드러내지 않은 것이다. 가우스나 르장드르를 비롯한 수학의 탐험가들은 18세기 후반, 거기서 한발짝 물러나 슬쩍 다른 길로 한발짝 내디뎠다. 바로 그 길은 소수 세계로 가는 매우 중요한 첫 발이었다 ! 바로 '소수의 밀도(density)'에 대해 관심을 기울인 것이다. 절대적인 그 무엇, 를 직접 드러내려는 욕심에서 어떤 자연수 n과 관계로 탐구의 방향을 바꾼 것이다. 밀도는 평균적으로 얼마나 자주 나타날까에 대해 말해준다.
로 쓸 수 있다. 앞의 예에서 나온 것을 보면 아래와 같다.
에 대한 절대적인 정보가 없기 때문에 그 분포도 절대적으로 정확히 알기는 힘들다. 소수는 몹시 불규칙하게 드러나는 것 같지만, 어떤 구간에서의 평균적인 분포인 밀도를 보게 되면 어느 정도의 규칙성을 드러낸다. 경험적인 방법으로 과 n의 관계를 포함한 소수에 관한 표를 만들어 보면서 가우는 '우연히' 이 값들이 에 매우 가까와진다는 것을 발견하였다. [14] 다음과 같이 표현할 수 있다.
또는
놀랍게도 자연수 세계의 함수인 가 해석학의 세계에서 중요한 역할을 하는 자연로그 함수와 매우 비슷한 성질을 갖는 것이다. 따로 발전해온 수학의 두 길이 하나로 만나는 중대한 사건이었다. (그 순간의 희열을 상상해보라!)
이제 정확한 은 아니더라도 실제와 매우 근사한 것을 유도할만한 근거가 생긴 것이다. 그 수학적 진실은 이해하기 간단해 보였으나 수학적으로 엄격하게 증명하는 것은 가우스 당시의 수학적 기법으로는 불가능하였다. 그것이 가능해진 것은 가우스가 있던 괴팅겐 대학의 젊은 수학자 리만의 공헌에 힘입어 가우스의 추측 이후 100여년이 지나 프랑스의 수학자들(아다마르, 발레-뿌셍,1896년)에 이르러서였다. 그 이후 이 증명은 수학적으로 더 엄격하게 보완되고 단순화되었다. (만골드, 란다우) 그리고 증명에서 쓰인 복소수의 성질을 이용하지 않고 새롭게 증명함으로써 이 분야의 연구게 기여하였다. (비너)
그러나 어쨌든 소수의 세계를 탐구하는 것은 여전히 어려운 일로 남아있다.
소수에 관하여 풀리지 않고 있는 문제들
아래의 네 문제는 1912년 세계 수학자 회의에서 E.란다우(E.Landau)가 '수론'에서 풀어야할 중요한 네 문제로 꼽은 문제들로 2006년이 저물어가는 현재 아직 풀리지 않고 있다.
 골드바흐 가설의 참거짓 문제
골드바흐 가설의 참거짓 문제
오일러가 수정한 골드바흐 가설 을 쓰면 다음과 같다.
- 골드바흐 가설 : 2 보다 큰 어떤 짝수도 두 소수의 합으로 나타낼 수 있다.
 쌍둥이 소수의 무한성 문제
쌍둥이 소수의 무한성 문제
(3,5), (11,13), (29,31) 처럼 소수인데 그 차이가 2가 나는 수들이 소수의 열에는 계속 등장한다. 그런 수들을 '쌍둥이 소수'라고 부르곤 하는데, 그렇다면 과연 이런 쌍둥이 소수들은 끝없이 많이 있을까, 아니면 어디선가 끝이 날까? 이 질문은 앞의 골드바흐 가설 문제와 깊이 연관된 것으로 보이는데 이에 관한 연구를 정리해보면 아래와 같다.
- n 과 n+2가 9개 이하의 소수의 곱으로 표현되는 수는 무한히 많다. (1919년, Brun, 앞의 논문에서)
- 앞의 9개가 7(1924년), 6(1930년), 5(1938년), 4(1957년), 3 (1962년)까지 줄어들게 됨
- 마침내 2개까지. (1973년) 다시 말하면 두 개의 소수들의 곱으로 된 수 n과 n+2, 다시 말해 '거의 쌍둥이 소수'인 수들은 무한개라는 것이 밝혀진 것이다.
 르장드르 가설
르장드르 가설
- 모든 자연수 n에 대하여 와 사이에는 항상 소수가 있다.[15]
 완전제곱과 하나 차이나는 소수
완전제곱과 하나 차이나는 소수
- p-1 이 완전제곱꼴인 소수 p는 무한개인가?
이제 쌍둥이 소수 문제나 골드바흐 가설 문제나 모두 는 증명 직전에 이르렀다고 볼 수 있는데 어쩌면 바로 지금이 막다른 길에 이른 것인지도 모른다. 지금까지와는 다른 어떤 새로운 사고의 틀이나 기법을 사용하여야 새로운 단계로 넘어갈 수 있을 듯.
Note
- ↑ 400 까지 직접 해볼 수 있는 프로그램이 있다. Java를 실현할 수 있다면 직접 해보라.
- 에라토스테네스 체 실현해 '보기'
- ↑ Hardy와 함께 연구 경력이 많은 20세기 정수론의 대가 J.E.Littlewood 의 제자. ; 현재 일리노이대 수학부 명예교수
- ↑ 현재 일리노이 대학 교수. 수학자. 프로그래머.
- ↑ 이 정리가 담긴 논문은 A.O.L. Atkin, D.J. Bernstein, Prime sieves using binary quadratic forms, Math. Comp. 73 (2004), 1023-1030. 인터넷에서 검색해서 다운 받을 수 있다.
- ↑ 1차 2변수 디오판테스 방정식은 명쾌한 알고리듬이 있다. 최대공약수 편을 참고하라.
- ↑ 마티야세비치는 해를 갖는 모든 디오판테스 방정식은 9개의 변수의 식으로 바꿀 수 있다는 사실을 밝혔다. 따라서 9 개 변수면 충분하다. 대신 방정식의 차수는 엄청나게 커진다.
- ↑ 그 방정식 묶음은 아래와 같다.
- ↑ 셀 수 있는 집합이란 자연수와 1:1로 대응하는 집합이라는 뜻이다. 이에 대해서는 유한집합, 무한집합이란 무엇인가? 를 참고하라.
- ↑ 마티야세비치의 결과와 그 유추 결론은 그 다항식 자체에 있는 것이 아니라 '계산가능함'이 '다항식들(polynomials)'로 표현된다데 의미가 있는 것이다. 이에 대하여 명확하게 이해하기 위해서는 수리 논리(알고리듬 이론)에 대한 지식이 필요하다. 계산가능성(computability)은 여러 언어로 표현될 수 있는데, 여기서는 그것이 '다항식 언어'를 통해서도 표현될 수 있음을 말하고 있다. 이는 계산복잡성(compuational complexity)에 관현 연구로 뻗어 나간다.
- ↑ 이에 대해서는 4n+1 꼴의 소수들 을 참고하라.
- ↑ 답이나 귓속말은 소수의 분포와 연관된 증명들 모음 을 참고하라.
- ↑ wikipedia에서 인용하였음.
- ↑ wikipedia에서 인용하였음.
- ↑ 자연로그 에 대해서 로그 연산 참고
- ↑ 러시아의 체브쉐프(Chevshev)는 어떤 자연수 n 에 대해서도, n 과 2n 안에는 소수가 있다는 사실을 밝혔다.
Related
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia












































