Geo Trans Construction: 두 판 사이의 차이

2007년 5월 1일 (화) 12:33 기준 최신판

작도 가능 으로

기하학적 변환의 작도

우리가 사는 세계에서는 경계가 분명하다. 국경이나 지방, 집들은 벽이나 철책 같은 것으로 경계가 분명하다. 하지만 수학의 세계에서 이런 구분은 엄격하지 않다. 수학의 세계가 추상적인 대상들과 그것들의 성질을 탐구한다는 점에서 구분이 엄격하지 않다는 것은 어쩌면 당연하다. 어떤 수학의 영역이 다른 수학의 영역과 깊이 연관되는 예는 많다.^[1] 역사적으로 수학은 그 대상별로 분화하고 통합해가면서 살아있는 세계로서 그 몸통을 드러낸다. 그러나 어찌되었든 전통적으로 그 탐구 대상에 따라 구분을 하기도 하는데 우리가 들어선 영역은 '기하학' 분야다. 산술이 '자연수'나 '정수'를 탐구의 대상으로 삼았던데 비해, 기하학은 점, 선, 면과 같은 기하학적인 대상들이 이루는 '도형'의 성질을 탐구하는 영역이다. 자연수 집합에서 자연수의 관계와 연산을 정의했듯, 기하학의 세계도 그런 관점으로 볼 수 있다. 보통 '합동' '닮음' 같은 것을 비교 관계로, '변환(transformation)' 을 함수적 연산으로 설명할 수 있다.

지금 우리가 관심을 기울이는 만남의 영역은 '작도가능'이다. 여기서는 기하학적 연산이라고 볼 수 있는 '변환'들 중 작도가능한 것을 보인다. 그 중 일부는 이미 앞에서 보았다. 변환이 작도 가능하다는 사실을 보이면 그 자체로 흥미로울 뿐 아니라 앞으로 어떤 기하학적인 문제를 맞닥뜨렸을 때, 그 문제가 작도가능한지 아닌지 보는데 힘을 덜 들이게 된다.

기하학적 변환

유클리드 공간에서의 변환만 하더라도 따로 주제를 정해 살펴볼만큼 덩어리가 큰 주제다. 근래는 수학의 기초 개념인 집합과 함수의 용어로 변환들을 설명한다. 여기서는 그것에 대한 세세한 논의는 하지 않고 알고 있는 대로 변환들을 직관적으로 받아들인 다음 그것들이 '자와 컴퍼스'만을 써서 어떻게 작도 가능한지 보고자 한다. 앞으로 유용하게 쓰일 기초적인 변환들을 보자. 용어를 정의하는데 조금씩의 차이가 있으므로 여기서는 작도 가능에서 필요한 기능들을 중심으로 이해하자.

지금부터는 원을 나타내는 기호를 통일하기로 한다. 다른 뜻은 없고 쓰기 편하기 위해서다. 중심이 O 고 반지름이 r 인 원은 $\Sigma (O,r)$ 로 나타내기로 약속한다. 특정한 성질을 띄는 점들의 집합을 도형이라 하는데, 어떤 도형이 주어져 대충 - 수학에서 좋아하는 표현이 아니지만 - 아래의 규칙에 따라 새로운 도형을 이룰 수 있는 경우들이 있다. 이들은 기하학에서 흔히 등장하는 변환들이다.

회전 : 어떤 점 O 를 중심으로 주어진 각 $\alpha$ 만큼 회전함. 길이 각은 변하지 않음. 위치만 정해진대로 바뀜.
대칭 : 주어진 점 O 나 또는 주어진 선 $l$ 에 대해 거울을 댄 듯 대칭함. 길이 각은 변하지 않음. 위치만 정해진대로 바뀜.
이동 : 길이를 유지하면서 평행하게 다른 자리로 옮겨감. 앞의 회전이나 대칭을 포함하는 개념.
확대와 축소 : 각을 유지하면서 주어진 비율로 길이를 늘이거나 줄임.
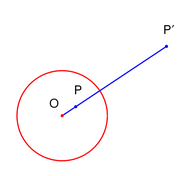
뒤집기 (inversion): 주어진 원 $\Sigma (O,r)$ 에대해 주어진 점이 P 라면 새로운 점 P'은 다음의 관계를 가지면서 변환.

|\ OP\ |\cdot |\ OP'\ |\ =r^{2}

이런 기초적 변환들을 이어서 쓴 (합성) 결과도 변환이라고 한다 : 다시 말해

위의 기초 연산들은 변환이다.
어떤 변환 f 와 변환 g 가 있을 때, 이것의 합성 $f\circ g$ 도 변환이다.

변환에 대해서는 더 엄격하게 정의할 수 있고 그 성질들을 보는 것 자체는 기하학에서 매우 흥미로운 분야이지만, 관심을 '작도가능'에 집중하기 위하여 직관적으로 이해하기로 한다. 여기서 중요한 것은 위의 앞의 '변환'들은 모두 작도 가능하다는 사실을 밝히는 데 있다. 더 일반적으로 말해서 affine 변환이나 projection 변환들은 모두 작도 가능하다. 각과 길이을 유지하는 변환들은 간단하다. 뒤집기 처럼 '원'이 직선으로 '직선'이 원으로 변하는 성질을 갖는 변환이나, 일반적으로 아핀 변환처럼 '길이와 각까지 변환'하는 경우(따라서 어떤 삼각형도 이등변 삼각형으나 정삼각형으로 변환할 수 있다.)는 작도가능을 보이는데 있어 눈에 띄게 풀이를 단순하게 해준다.

뒤집기(inversion) 의 기초성질

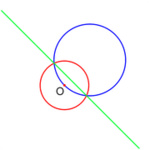
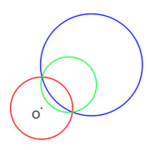
더 넘어가기 전에 뒤집기(Inversion)에 대해 몇가지 기초적인 사실을 알아둘 필요가 있다. 원의 중심은 뒤집기 연산의 정의역에서 빠진다는 사실에 주목하라. 정의에 따라 중심 0 를 변환시킬 수 없기 때문이다. ^[2]

정의에 따라 따져가면, 어떤 주어진 원 $\Sigma (O,r)$ 에 대해 뒤집기 변환을 할 경우,

주어진 원 안의 점들은 원 밖으로 뒤집힌다.
원의 점들은 변하지 않는다.
직선 $l$ $l$ 이나 원 $\Sigma (C,a)$ $\Sigma (C,a)$ 을 뒤집으면
- 원의 중심 O 를 지날 때는 직선으로 바뀐다. (오른쪽 그림 : 중심을 지나는 원은 직선으로)
- 그렇지 않으면 원으로 뒤집힌다. (오른쪽 그림 : 중심을 안지나는 원의 뒤집기는 원으로)

여기까지는 주어진 도형을 뒤집기 하면 꽤 심하게 변한다는 사실을 알 수 있는 부분이다. 뒤집기가 어떤 도형을 마냥 심하게 바꿔서 중요한 성질들을 흩트려버린다면 이 변환을 통해 얻을 것은 별로 없었을 것이다. 이어지는 다음의 사실은 뒤집기의 안정적 성질에 대해 말해주고 있다. 뒤집기를 해서 주어진 도형의 모양은 비록 직선에서 원으로 변할 수 있지만, 바뀌지 않는(invariant) 중요한 성질들이 있다.

뒤집기 전에 두 도형의 교점은 뒤집은 다음에도 교점으로 남는다.
주어진 두 직선의 교점에서 두 직선으로의 각은 뒤집어도 변하지 않는다. 이때 원과 직선이나 다른 원과의 교점에서의 각은 그 점에서 접선의 각으로 정의한다.

따라서, 예를들어 보면, 주어진 원의 밖에서 뒤집기 전에 직선과 직선의 교점이 있었다면 이를 뒤집을 경우, 원과 원으로 바뀔 수 있지만, 주어진 원 안에서 '한점에서 만난다'는 성질은 그대로 이어지고, 교점에서 두 직선이 이루었던 각도 유지된다.

기초 변환(연산)들의 작도 가능

위의 변환들은 모두 작도 가능하다. 이는 앞으로 우리가 어떤 '작도 가능' 문제를 보일 때 풀이를 매우 단순하게 하는데 도움을 준다.

회전 : 작도 가능의 기초 에서 보았듯, 어떤 각이 정해지면 주어진 직선에서 그 각과 같은 각을 작도할 수 있으므로 회전은 작도 가능하다.
이동 : 주어진 도형에 대해 평행선을 그을 수 있으므로 이동은 작도 가능하다. (원은 그 접선들의 평행이동으로 받아들이면 된다.)
대칭 : 주어진 선분에 수직인 선을 그을 수 있고, 정해진 길이만큼 이동할 수 있으므로 작도 가능하다.
확대와 축소 : 어떤 점에 대하여 평행 이동하면서 정해진 길이만큼 곱하거나 나누는 선분을 작도할 수 있으므로 작도 가능하다.
뒤집기 : 앞의 그림에서 볼 수 있듯이 다음의 단계를 거쳐 주어진 점 P는 Inv(P) = P'인 P'로 변환한다.

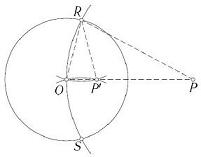
뒤집기의 작도가능함은 작도 가능 문제를 풀 때 폭넓게 쓰일 수 있다. 뒤집기라는 강력한 도구는 우리가 어떤 작도 가능문제에 부딪혔을 때 해결하는데 드는 힘을 확 줄여준다. 앞으로 그 사실을 몇 번 확인할 수 있을 것이다. 아래에서, 작도를 해서 얻은 점이 처음 주어진 점의 뒤집힌(inverted) 점이라는 사실을 직접 확인하라.

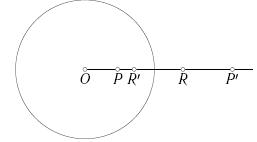
주어진 원 $\Sigma (O,r)$ $\Sigma (O,r)$ 의 바깥쪽에 있는 점 P 는 원 안의 점 P'로 뒤집히는 작도.
- 새로운 원 $\Sigma (P,|\ PO\ |)$ 를 작도하고 $\Sigma (O,r)$ 과 $\Sigma (P,|\ PO\ |)$ 의 교점 R, S를 얻는다.
- 새로운 원들 $\Sigma (R,r),\Sigma (S,r)$ 을 작도하고 두 원의 교점 중 중심 0 가 아닌 새로운 점 P'를 얻는다.

원 밖의 어떤 점을 원안으로 뒤집는 작도를 할 때 컴퍼스 만으로 작도가능하다

위의 모든 작도는 컴퍼스만 써도 된다는 것을 주목하라.

주어진 원 $\Sigma (O,r)$ $\Sigma (O,r)$ 의 안 쪽에 있는 점 P는 원 안의 점 P'로 뒤집히는 작도.
- 주어진 두 점 O,P 를 지나는 반직선을 작도한다.
- 주어진 원의 바깥쪽에 위치하도록 선분 $|\ OP\ |$ 의 n배한 점 R 을 잡는다. (이 작도를 과연 컴퍼스 만으로 작도할 수 있을까?)
- 앞의 '바깥쪽'의 점을 안으로 뒤집는 작도를 하였듯이 R 을 뒤집어 R'를 얻는다.
- $|\ OR'\ |$ 를 n 배한 점 P'를 작도한다.

여기서 자가 쓰인 유일한 곳은 처음 단계인 반직선을 작도하는 부분이다. 만약 우리가 굳이 작도하지 않고 주어진 그런 반직선이 있는 것으로 가정하고 그 점 R 의 위치를 알 수만 있다면, '자로 선을 직접 그리지는 않았지만' 분명히 그 점 R 은 작도가능하다. 그렇다면 앞의 괄호에서 질문하였듯이 R 을 작도할 때, 자를 쓰지 않고 작도할 수 있을까?

문제의 핵심은

두 점 O 와 P 를 잇는 반직선에 있고 중심 O 에서 선분

|\ OP\ |

의 n 배의 길이를 갖는 점.

라는 두가지 특별한 성질을 어떻게 컴퍼스만으로 작도할수 있느냐에 있다. ^[3] 이것만 가능하다면 다음과 같이 말할 수 있다.

원 안의 어떤 점을 원 밖으로 뒤집는 작도를 할 때도 컴퍼스 만으로 작도가능하다. 다시 말해, 뒤집기 변환은 컴퍼스만 써서 작도 가능하다.

가능하다. 과연 어떻게 ?

변환을 이용할 수 있는 작도 문제

위의 변환 개념을 써서 작도할 수 있는 예를보자. 어떤 문제가 작도 가능하다는 것을 보이는 방법은 물론 한가지가 아니다. 여기서 든 방식이 아닌 다른 방법들이 있을 수 있다. 여기서는 변환을 이용할 경우의 문제들을 예시하였다. 여기서 든 예말고도 앞으로 '변환'의 작도가능은 자주 나타날 것이다.

밑변이 a, 높이가 h 이고 아랫변이 각의 차이가 $\alpha$ 가 되는 삼각형 ABC를 작도하라. (밑변을 BC로 한다.)
두 원 $\Sigma _{1},\Sigma _{2}$ 이 주어졌을 때, 삼각형의 한 꼭지점 B는 $\Sigma _{1}$ 에, 다른 꼭지점 C는 $\Sigma _{2}$ 에 있고 $|\ AB\ |=|\ AC\ |$ 인 이등변삼각형을 작도하라.
어떤 '작도 가능한' 선분의 길이 m이 주어졌다고 하자. 그리고 원 $\Sigma$ 이 주어지고 원에 속한 점 A, B가 주어졌고 원 밖에 직선 $l$ 이 주어졌다. 그럴 때 직선 AX와 직선 $l$ 이 만나는 점과 직선 BX와 직선 $l$ 이 만나는 점 Q의 길이가 m이 되도록 하는 원 위의 어떤 점 X를 작도하라. (기호로 쓰면 $\{X\ |\ m=|\ AX\cap l\ \ BX\cap l\ |\}$ ) ^[4]
어떤 '교차하는' 두 직선 $m,l$ 들과 이 직선들에 속하지 않은 점 A이 주어졌다. 어떤 선분의 길이 k도 주어졌다. A로 부터 어떤 직선을 작도하여 그 직선들이 만나는 점을 AM, AL 이라 하자. 두 점의 관계가 아래와 같게 하는 직선 n을 작도하라. ^[5]

{\frac {|AM|}{|AL|}}=k

직선 $l$ 과 그 직선 밖에 두 점 A, B 가 주어졌을 때, 그 두 점을 지나고 $l$ 과 접하는 원을 작도하라.
(Appolonius 작도) 주어진 세 원 $\Sigma _{1},\ \Sigma _{2},\ \Sigma _{3}$ 에 접하는 원을 작도하라. (WIM Ch3. 6절의 2)

Note

↑ 전체적으로 그런 증거들이 자주 등장하기도 하거니와, 이를 따로 모아볼 수도 있다. 그 중 일부는 아름답다 수학식 에 모아가고 있다. 해석 기하, 대수 기하와 같이 기존에 있던 수학의 영역들이 통합되는 지점에 새로운 수학의 영역이 생기기도 하고 수학의 영역 자체가 더 기초적인 분야에서 여러개의 영역을 통합하기도 한다. 사실, 수학은 하나다.
↑ 유클리드 평면( $\mathbb {E}$ ) 에 우리가 새로운 점 '무한점'을 추가하면 이 기하학의 평면은 이미 유클리드 평면보다 확장된 공간이다. 자연수에 0 을 추가하듯이. 또는 0 을 포함한 자연수에 -1 을 추가하여 정수를 정의하듯이, 또는 실수에 i 를 추가하여 복소수 공간으로 확장해나가는 것과 논리적인 차이는 없다.
↑ 작도가능을 정의할 때 주어진 선분에 아무 점이나 찍어 새로운 점을 얻을 수 있다고 했지만 그것은 '아무점이나' 찍는 것이지 어떤 성질을 만족하는 특별한 점은 아니다.
↑ 물론 더 엄격하게 쓰면, 어떤 작도가능한 선분의 길이들의 집합을 $C$ 이라고 쓴다면
$\forall m\in C,\ \forall l\ ,\ \forall \Sigma ,\ \forall A,B\in \Sigma ,\ \exists X\in \Sigma (|\ AX\cap l\ ,\ BX\cap l\ |=m)$
↑ 기호로 바꿔 쓰면
$\forall k\in C,\ \forall l,m,\ \forall A\notin l,m,\ \exists n(A\in n\quad \land \quad {\frac {|\ AM\ |}{|\ AL\ |}}=k)$

[1] 전체적으로 그런 증거들이 자주 등장하기도 하거니와, 이를 따로 모아볼 수도 있다. 그 중 일부는 아름답다 수학식 에 모아가고 있다. 해석 기하, 대수 기하와 같이 기존에 있던 수학의 영역들이 통합되는 지점에 새로운 수학의 영역이 생기기도 하고 수학의 영역 자체가 더 기초적인 분야에서 여러개의 영역을 통합하기도 한다. 사실, 수학은 하나다.

[2] 유클리드 평면( $\mathbb {E}$ ) 에 우리가 새로운 점 '무한점'을 추가하면 이 기하학의 평면은 이미 유클리드 평면보다 확장된 공간이다. 자연수에 0 을 추가하듯이. 또는 0 을 포함한 자연수에 -1 을 추가하여 정수를 정의하듯이, 또는 실수에 i 를 추가하여 복소수 공간으로 확장해나가는 것과 논리적인 차이는 없다.

[3] 작도가능을 정의할 때 주어진 선분에 아무 점이나 찍어 새로운 점을 얻을 수 있다고 했지만 그것은 '아무점이나' 찍는 것이지 어떤 성질을 만족하는 특별한 점은 아니다.

[4] 물론 더 엄격하게 쓰면, 어떤 작도가능한 선분의 길이들의 집합을 $C$ 이라고 쓴다면
$\forall m\in C,\ \forall l\ ,\ \forall \Sigma ,\ \forall A,B\in \Sigma ,\ \exists X\in \Sigma (|\ AX\cap l\ ,\ BX\cap l\ |=m)$

[5] 기호로 바꿔 쓰면
$\forall k\in C,\ \forall l,m,\ \forall A\notin l,m,\ \exists n(A\in n\quad \land \quad {\frac {|\ AM\ |}{|\ AL\ |}}=k)$

[1]

[2]

[3]

[4]

[5]