Conic Section Def: 두 판 사이의 차이

2007년 11월 21일 (수) 21:36 기준 최신판

이 page는 앞으로 많이 보태질 계획입니다. 누구나 글을 쓸 수 있습니다. 정성을 모아주십시오. ( 수학식 쓰기)

엄격하지 않게 말하면, Conic Section(원추단면)은 cone(원추)를 평면으로 잘라내어 생긴 교차점들의 집합을 뜻한다. 고대 그리스 이후 순수하게 수학적 흥미로서만 아니라 다양한 문제를 해결하는 데 응용되기 때문에 오랫동안 연구가 활발하였다. 아래 응용의 예를 모았다.

역사

Conic Section에 대한 연구는 고대 그리스의 기록들에도 남아있다. 앞의 응용 부분에도 나와 있듯이 이미 기원전 5세기 경 메네무크스는 원추 단면들의 도형들의 성질을 빌어 Doubling Cube 문제를 해결하였다. 고대, 중세, 근대, 현대 까지 연구가 끊이지 않았지만, 아폴로니우스의 '원추에 대하여' 라는 저작은 그 중에서도 가장 빛나는 기념비적인 작품이다. 이 저작은 총 8권으로 되어 있는데 오늘날 7권이 전한다. 여기에는 중요한 정리가 약 400여개 있는데 그 연구가 워낙 방대하여 오늘날에도 의미있는 새로운 정리를 보태는 것이 희귀할 정도다. 이 책은 유클리드의 '원론'과 더불어 기하학에서 가장 많이 읽혔던 책일 것이다.

Conic Section 이라 할 때 보통 3 형태의 아래 곡선을 말한다.

타원(ellipse)
쌍곡선(hyperbola)
포물선(parabola)

원은 타원의 특수한 경우로 볼 수 있으므로 따로 말하지 않아도 된다. 물론 평면이 Conic의 꼭지점을 지날 때는, 자르는 평면의 각도에 따라 두 직선, 또는 한 직선 또는 점이 나올 수 있다. 이 특별한 곡선들을 정의하는 방법은 여러가지이고 그것들은 모두 등가인데, 아래에서는 이에 대해 살펴보자.

정의 1 : Conic Section

아래 어떤 cone 을 만드는 방법은 모두 '공간'에서 이루어진다는 것을 전제한다. 어떤 것이든 cone 의 결과는 같다.

원추 만들기 1 : 직선들의 집합

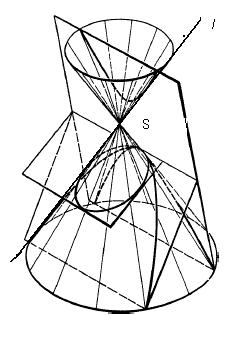
먼저 cone '원추'를 다음과 같이 정의한다.

한 점 A와 그 점을 지나는 직선 을 정한다. 그리고 직각 보다 작은 각 $\theta$ 를 정한다.
점 A를 지나고 직선 $l$ 과 $\theta$ 을 이루는 직선
위의 조건을 만족하는 모든 직선의 집합은 cone을 이룬다.

이 집합은 직선 $l$ 에 점 A 에서 $\theta$ 각으로 직선을 하나 더 정하고 그것을 $l$ 을 축으로 회전한 것과 같다. 여기서 cone은 주어진 점 A 과 그 점을 지나는 직선 $l$ 을 기준으로 정의^[1] 된다는 점을 주목하자. 따라서 점 A 에 대칭인 두 원추 모양이고, 밑이 무한대로 뻗어나가므로 정확한 의미에서의 원추는 아니다.

Q : 앞에서 '직각보다 작은 각을 정의한다고 했는데, 직각보다 크다면 ? :)

원추 만들기 2 : 아폴로니우스

종합 기하학의 거장 아폴로니우스는 타원이나 포물선, 쌍곡선을 다음과 같이 정의했다. 여기서는 간단히 타원만 보도록 하자.

중심이 O 인 원 $\Sigma$ 이 있다고 하자. 중심 O 에서 수직으로 '올리자'.
그 반직선 중 한 점 A 를 정하자.
점 A 와 원의 모든 점을 '직선'으로 연결하자.

원추 단면

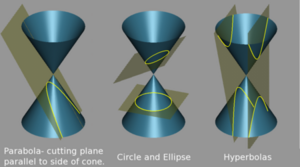
이제 평면으로 A를 지나지 않도록 우리가 정의한 원추를 교차시킨다. (자른다) 3 종류의 도형을 얻을 수 있다.

타원 : 대칭인 원추들 중 한 쪽만 자르되 직선들의 집합 중 어떤 직선과도 평행하지 않도록 자를 경우 평면과 원추의 교집합
쌍곡선 : 양쪽을 모두 자를 경우 평면과 원추의 교집합
포물선 : 직선들의 집합 중 어떤 한 직선과 평행하게 (축과 각 $\theta$ 로) 자를 때 평면과 원추의 교집합

물론 원을 얻을 수도 있지만 우리는 원을 타원의 특수한 경우로 보았으므로 세 유형이라고 할 수 있다. 그리고 꼭지점 A 를 지나게 자를 경우엔 다음과 같이 될 것이다.

자르는 평면이 꼭지점만 지날 경우 한 점
자르는 평면이 원추의 직선과 접할 경우 한 직선
자르는 평면이 원추의 직선과 교차할 경우 두 직선의 쌍

정의 2 : 거리의 합과 차

타원 : 주어진 두 점 $F_{1},F_{2}$ 에서 어떤 점까지의 거리의 합이 c 인 점 M 들의 집합 : $\{M|MF_{1}+MF_{2}=c\}$ ^[2]

정의 3 : 대수적 표현

정의 4 : Projective(투사,사영) 개념을 이용한 정의

Conic Section 과 중력

Euclid and other Greek geometers made an extensive study of the conic sections - curves created by intersecting a cone and a plane. These are the ellipse, the parabola and the hyperbola.

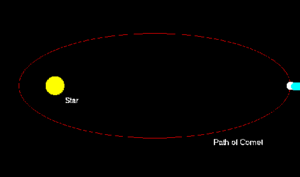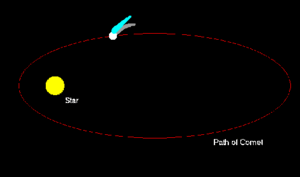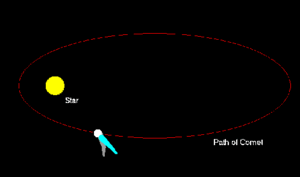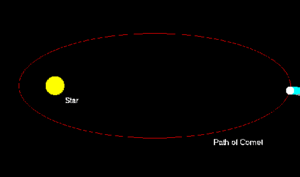
오른쪽 그림은 혹성이 지구 주위를 돌고 있는 것을 형상화한 것이다. 타원과 매우 비슷한 형태로 공전하고 있다.

This turned out to facilitate the work of Galileo, Kepler and Newton in the 17th Century, as these curves accurately modelled the movement of bodies under the influence of Gravity.

Bodies moving with less than escape velocity travel in a parabolic trajectory and fall back to earth;
Bodies moving at escape velocity move in a perpetual elliptical orbit;
Bodies with an oblique approach to a celestial body at greater than escape velocity will follow a hyperbolic trajectory and not return;

Contemporary demonstrations of these paths for bodies moving under gravity would usually be performed using the techniques of analytical geometry (aka co-ordinate geometry or Cartesian geometry) and differential calculus, which readily provide straightforward proofs. Of course these techniques had not been invented at the time that Galileo investigated the movement of falling bodies. Once he had ascertained that bodies fall to the earth with constant acceleration, he proved that projectiles will move in a parabolic path using the procedures of Euclidean geometry.^[3]

다르게 했지만, 같은 도형을 정의한다

원추 단면을 쓴 정의와 거리의 합-차를 쓴 정의의 등가

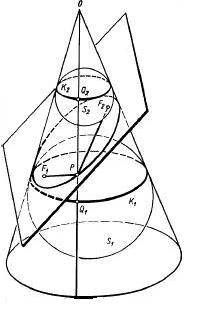
여기서는 원추 단면으로 얻은 도형은 거리의 합과 차로 얻은 도형이 될 수 밖에 없다는 것을 보일 것이다.

Dandelin^[4]의 증명이다. 우선 타원만 보기로 하자.

원추 꼬깔 안에 두 개의 구가 있다고 하고, 정점 O 에서 직선을 내렸을 때, 두 구가 접하는 점을 $Q_{1},Q_{2}$ 라 하자. 그 직선은 축을 따라 구 주위로 회전한다.
두 구에 점들 $F_{1},F_{2}$ 에 접하도록 평면으로 잘라낸다.
잘라내는 면과 원추가 만나는 점들을 이으면 어떤 도형이 될 것이다. 그 도형 위의 점을 아무 점이나 P 라 하자.
점 P 에서 $F_{i}$ 으로 잇거나, $Q_{i}$ 으로 잇거나 한 점에서 같은 구로 접선이므로 $PF_{i},PQ_{i}$ 의 길이는 같다. (i = 1,2)