Doubling Cube

작도 가능 으로

Doubling the Cube

전설 하나. 에라토스테네스(Eratosthenes) 가 전하는 전설을 따르면 큐빅의 부피를 두 배로하는 큐빅을 만드는 문제의 시작은 다음과 같다고 전해진다.

" 에게해에 있는 델로스에 전염병이 돌았다. 신의 분노라고 생각한 사람들은 태양의 신 아폴론 신전에가서 신탁에 물었다. - 어떻게 하면 전염병을 멈출 수 있을까요? 신탁(오라클)은 큐빅 모양이었던 금으로 된 제단의 부피를 두 배로 하면 된다는 답을 주었다. 사람들은 금을 모아 같은 모양의 큐빅을 하나 더 만들어 쌓았다. 그런데도 전염병은 멈추지 않았다. 사람들은 다시 신탁에게 가 물었다. - 신의 말씀을 따랐는데 왜 전염병이 멈추지 않는걸까요? 신탁은 답했다. "그대들은 말을 잘못이해했소. 제단의 모양을 바꾸지 않으면서 부피를 두 배로 해야한단 말이오." 이 문제를 어떻게 풀어야 할지 몰라 사람들은 유명한 현자 플라톤을 찾아갔다. 플라톤은 답했다. " 아마 그대들이 기하학을 공부하지 않는 것에 신들이 분노했나봅니다." 그러나 이렇게 답을 한 플라톤도 자와 컴퍼스를 써서 마땅한 답을 내지는 못했다.

그때 이후로 큐빅의 모양을 유지하면서 부피를 두 배로 하는 문제는 '델로스 문제'라고도 불려오기도 한다. 이 문제를 직선과 원을 그릴 수 있는 도구만 써서 풀 수 있겠는가 하는 문제는 작도가능의 고전적 3 대 문제 중 하나가 되었다. 고대 그리스시대에도 이 문제가 자와 컴퍼스만 써서는 풀 수 없다고 인식한 것으로 보인다. 지금까지 알려진 해법들은 모두 '자와 컴퍼스 이상'의 어떤 도구를 썼다. 표준적인 자와 컴퍼스보다 복잡한 도구들을 써서 풀어낸 방법은 고대 그리스 이후 해법이 한두가지가 아니다. 여기서는 우선 고대 그리스의 가장 빛나는 결과라고 여겨지는 해법 둘을 먼저 본다.

• 아르키타스(Archytas,또는'아르히트')의 해법 : 원기둥, 원추, 원고리의 교점과 비례 관계를 이용한 해법
• 메네크무스(Menaechmus, 또는 '메네흠')의 해법 : 원추 단면의 곡선(쌍곡선과 타원)을 이용한 해법

고대 그리스에 많은 해법들이 있었지만, 문명의 축이 인도와 아랍으로 옮겨가있던 천년이상의 시기는 상대적으로 덜 알려졌다. 이 시기는 지금의 아랍권이 문명을 찬란히 꽃피웠던 시기다. 고대 그리스의 저서들을 아랍어로 번역되었고 연구를 이어가면서 수학 탐구의 중심축이 아랍으로 넘어갔다. 나중에 새로운 중심축이 된 근대 유럽의 성과라도 알려진 것 중 여러개가 이미 이 당시에 발견된 흔적이 있다는 것이 밝혀지고 있다. 아랍에서는 대수(Algebra)적 언어가 주로 정립되어가던 시기였다. 고대 그리스의 수학적 성과를 번역하고 연구를 이어가던 아랍 문명은, 작도 3 대 문제를 비롯한 기하학 문제 또한 대수적 언어로 나타내게 된다. 12 세기 전후로 유럽은 원본을 잃고 아랍어로 번역되었거나 저술된 수학책들을 다시 들여온다. 이를 당시 학계의 공용어였던 로마어로 번역하면서 '대수화된 기하학'을 받아들이게 된 것이다.

17세기 초중반 데카르트는 그의 저서 '기하학'에서 기하학을 대수적으로 푸는 해석기하의 연구를 진행하여 이미 세제곱해서 유리수가 되지 않은, 3차 방정식의 근을 찾아야 하는'델로스 문제'에는 해가 없을 것이라고 추정했다. 마침내 1837년 프랑스의 완첼(Wantzel)이 이를 증명한다. 19세기 갈루와, 아벨, 데데킨드 등이 기초한 그룹, 링, 필드와 관련한 보다 추상적이고 (따라서) 일반적인 대수학이 정립되면서 일반화된다. 이런 수천년의 흐름을 여기서는 주마간산으로 둘러본다.

우선 고대 그리스로 돌아가고 (아쉽게도 아랍의 성과는 뛰어 넘고), 근대적 성과 까지 보자. 작도 불가능성 에서 더 근대적 시기의 개념으로 이 문제를 다시 만나게 될 것이다.

아르키타스 이전

주어진 큐빅의 모양을 바꾸지 않으면서 부피를 두배로 하는 문제를 현대의 대수 방정식 언어를 쓰면 간단하게 표현할 수 있다. 주어진 큐빅의 한 변의 길이가 a 이고 우리가 찾아야 할 큐빅의 한변의 길이가 x 라면 큐빅의 부피는 한 변의 세제곱이므로 대수적으로는

$x^{3}\ =\ 2a^{3}$

이 참이 되는 x 를 찾으라는 문제이며, '작도 가능'의 관점에서는 자와 컴퍼스 처럼 직선과 원만을 그릴 수 있는 도구를 써서 x 라는 선분의 길이를 작도할 수 있는가 하는 문제가 된다. 그런데 고대 그리스에서 모든 수학은 기하적 언어와 일상어로 탐구했을 뿐, 위와 같이 간편하게 대수식으로 나타낼 대수 언어가 없었다. 따라서 큐빅을 두배로하는 문제를 어떻게 '수학적으로 제대로 질문할 것인가' 하는 문제 조차 아직 정립되지 않았다. 이 한계를 뛰어넘게 한 사람이 바로 히포크라테스다. 그는 큐빅을 부풀리는 문제를, 지금의 언어로 해서 쓰면, 기하적 '비례'의 개념으로 다음과 같이 단순화하였다

길이가 a 인 선분이 주어졌을 때, 길이가 두 배 2a 인 선분을 작도 하고, 다음의 관계가 성립하는 x,y를 찾으면 그때의 x가 찾는 선분의 길이가 된다.

${\frac {a}{x}}={\frac {x}{y}}={\frac {y}{2a}}$

따라서 이 문제는 그런 관계가 성립하는 x, y를 찾기만 하면 충분하다. 그러나 이런 x와 y를 자와 컴퍼스만을 써서 찾지는 못했다. 그런데, 주어진 a 에 대해 위의 관계가 성립하는 x를 찾으면 그 x가 부피를 두배로 하는 큐빅의 한변인 x 일까?

${\frac {a}{x}}={\frac {x}{y}}={\frac {y}{2a}}=k$

라 하면

$k^{3}=\left({\frac {a}{x}}\right)^{3}={\frac {a}{x}}\cdot {\frac {x}{y}}\cdot {\frac {y}{2a}}={\frac {1}{2}}$

다 ! 또는 다음과 같이 '더 대수적으로' 해석할 수도 있다. 위의 네 선분들의 비례 관계식을 대수 언어로 풀어 해석해보면

$x^{2}=ay,\ y^{2}=2ax$ 또는 $2a^{2}=xy,\ x^{2}=ay$

도 된다. 어떤 것이든 등식의 성질에 따라, 예를 들어, 첫번째를 풀면

$x^{4}\ =\ 2a^{3}x$ 이고 따라서 $x(x^{3}-2a^{3})\ =\ 0$

이다. 따라서

$x\ =0$ 이거나 $x^{3}-2a^{3}\ =\ 0$ 다.

첫번째 경우는 선분의 길이가 0 으로, 이는 아폴론 신전의 제단을 없애는 것이니 전설대로라면 전염병은 더 창궐할 것이다. 따라서 해가 될 수 없고,

$x={\sqrt[{3}]{2}}a$

가 해다. 따라서 지금으로부터 2500년 전 경에 이미

${\sqrt[{3}]{2}}$

를 자와 컴퍼스로 작도할 수 있으면 큐빅 부풀리기 문제는 작도가능한 것으로 문제를 명쾌하게 단순화 시킨 셈이다.

아르키타스의 해법

아르키타스는 군통솔권자였고 플라톤의 절친한 친구였으며 플라톤을 죽음으로부터 구출한 사람으로 알려졌다. 또한 아르키타스는 당시 그리스 대부분의 도시에서 추방당했던 피타고라스 학파들이 활동하도록 허가한 피타고라스 학파의 한사람으로 추정된다. 아르키타스가 한 업적도 놀라운데, 가장 놀라운 결과는 '큐빅의 모양을 바꾸지 않으면서 부피를 두배로하는 문제의 해를 찾아낸 것이다. 아울러 그는 앞에 히포크라테스가 도달한 '비례'와 그 일반화를 비롯해 수론에서도 놀라운 업적을 보였다고 한다. 그 업적들이 나중에 유클리드의 '원론'의 수론에 해당하는 부분(8권) 에 실렸다. 그리고 피타고라스 학파가 중요하게 여겼던 음악이론의 대가였으며, 새로운 발명에 수학적인 모델을 적용한 사람이었고, 어린이들을 위해 장난감을 만드는 것을 좋아하였다.

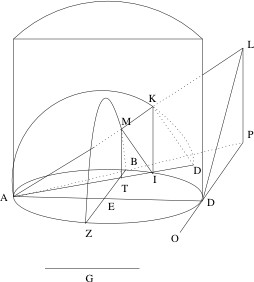
아르키타스의 해법은 지금의 시각으로 봐도 놀랍기 짝이 없다. 그의 해법을 보자.

• 두 선분 AB, AD 가 주어졌다고 하자. 그리고 선분 AB가 더 짧다고 하자.
• AD를 지름으로하는 원 S 을 그린다.
• AD 선분의 끝, D에 접하는 직선 o 을 그린다.
• AB를 연장하여 직선 o 과 만나는 점 P를 얻는다.
• 원 S를 밑으로하는 원기둥을 그린다.
• 선분 AP를 한변으로 하고 AD를 중심으로 회전하여 원추를 그린다.
• 원 S 를 AD를 중심으로 90도 회전하여 새로운 원 S'를 얻는다.
• 원 S'를 A를 지나는 원기둥의 직선을 중심으로 회전하여 원고리를 얻는다.
• 원기둥과 원추와 원고리가 만나는 점 중 하나를 K로 얻는다.
• 점 K에서 원 S로 투사(projection)하여 만나는 점 I을 얻는다.
• 선분 AD에 수직이고 B를 지나는 직선을 그어 원 S와 만나는 점 Z를 얻는다.
• 선분 BZ로부터 수직인 직선을 그어 (projection) 직선 AK와 만나는 점 M를 얻는다.
• AI의 연장선이고 AD와 길이가 같은 점 D'를 얻는다.

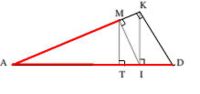
• 선분 AI, 다시 말해, 원 S 위의 점 I가 우리가 찾던 점이다.

히포크라테스가 제안했던 선분 x, y 를 작도할 수 있게 된 것으로 '큐빅'문제를 해결한 것이다.

• 조금 상세한 설명, 증명

Q. 옆의 그림을 과연 자와 컴퍼스로 작도할 수 없는 것일까? 그림을 보면서 다음을 생각해보자.

큐빅의 한 변의 길이가 AD로 주어졌다고 하자. AD의 반이 되는 점을 중심으로 하고 그 길이를 반지름으로 하는 원을 그린다. D에서 반원에 어떤 점을 잡아 K라고 하고 DK를 잇고 AK를 잇는다. 점 K에서 선분 AD에 수직으로 내리고 교차하는 점을 I라고 놓는다. 점 I에서 선분 AK에 수직으로 직선을 긋고 교차하는 점을 M이라 한다. M에서 다시 선분 AD에 수직으로 내려 교차하는 점을 T라 한다. 그렇다면 이는 다음을 말해주고 있다.

$|AM|:|AI|\ =\ |AI|:|AK|\ =\ |AK|:|AD|$

따라서,

$\left({\frac {|AM|}{|AI|}}\right)^{3}={\frac {|AM|}{|AD|}}$

이므로, 만약 2 |AM| = |AD| 라면

$2|AM|^{3}=|AI|^{3}$

으로 선분 AD의 길이의 반을 작도할 수 있으니, ${\sqrt[{3}]{2}}$ 를 작도할 수 있다. (과연 어디에 잘못이 있는가?)

메네크무스의 해법

수학적으로 더 명쾌하게 단순화한 히포크라테스의 혜안을 이야기하면서 말했듯이, 길이가 a인 선분이 주어진다면 우리는 다음 관계가 성립하는 x , y 를 찾을 경우 원하는 해를 찾을 수 있다.

$x^{2}=ay,\ y^{2}=2ax$

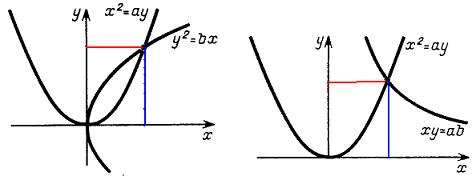
의 두식을 모두 만족할 때, 또는

$2a^{2}=xy,\ x^{2}=ay$

의 두 식을 모두 만족할 때다. 다시 쓰면

$\forall a\ \exists x\ [(x^{2}=ay\ \land \ y^{2}=2ax)\ \quad \lor \quad (2a^{2}=xy\ \land \ x^{2}=ay)]$

위 두 식을 지금의 방식으로 하면 아래 조건을 만족하는 두 포물선의 교점 $(x,y)$

$\forall a\ \exists x\ (x^{2}=ay\land y^{2}=2ax)$

을 찾거나, 아래 조건을 만족하는 포물선과 쌍곡선의 교점 $(x,y)$

$\forall a\ \exists x\ (2a^{2}=xy\land x^{2}=ay)$

을 찾는 문제다. 고대 그리스 시대에는 이런 식으로 간편하게 표현하는 언어가 발달하지 않았다. 다만 '쌍곡선' '포물선'을 작도할 수 있다면, 다시말해 쌍곡선, 포물선의 점들을 구할 도구를 써서 얻어낼 수 있다면, 그 도구를 이용하여 큐빅문제가 해결된다는 것을 암시한다. 따라서 문제는 그런 곡선을 작도할 도구가 과연 있느냐에 달려 있다. 이에 대한 답은 원추의 성질과 큐빅 문제를 연구하던 메네크무스가 냈다. 대학자 유독수스(Eudoxus ; 408 BC - 355 BC ) 의 제자라고 전해지기도 하는 그가 다양한 형태의 원추와 그것을 자르는 방법에 따라 쌍곡선, 포물선, 타원을 얻을 수 있다는 것을 밝힌다.

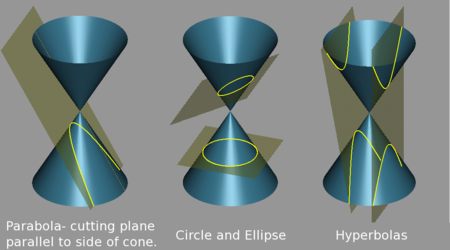
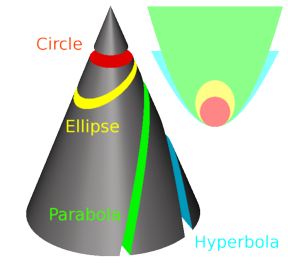
메네크무스는 회전각의 크기에 따라 둔각, 직각, 예각의 원추를 생각했다. 마주보는 두 변이 이루는 각의 크기가 직각보다 크면 둔각, 작으면 예각 원추라고 한다. 그때, 변에 직각으로 단면을 내면 원추의 표면에는 곡선이 나타날 것이다. 둔각 원추의 경우는 쌍곡선을, 직각 원추는 포물선을, 그리고 예각 원추는 타원 모양을 띤다.

플루타르크에 따르면, 플라톤은 메네크무스의 '원추 절단' 방법을 통해 얻은 곡선의 교점으로 위의 히포크라테스의 비례문제에서 x, y를 찾아가는 시도를 '비기하학적'이라고 비판하였다고 한다. 어찌 되었든 메네크무스가 '큐빅 문제'를 풀기 위해 찾아낸 원추 단면에 대한 연구는 그 뒤 기하학(수학)의 연구에 중요한 역할을 하였다.

Conic Section

포물선, 원-타원, 쌍곡선‎

그리고 ...

고대 그리스에서 이미 작도 고전 3대 문제에 대해 자와 컴퍼스만으로 작도할 수 없음을 알았을 것이라고 짐작하는 증거 중 하나로 알렉산드리아의 파푸스(Pappus;AD 290-350)의 결과를 들 수 있다. 그는 작도 문제를 아래와 같이 세가지로 분류하였다.

• 평면적 작도 : 직선과 원만으로 작도하는 문제 (자와 컴퍼스 작도 문제)
• 공간적 작도 : 포물선, 쌍곡선, 타원으로 작도하는 문제 (원추 절단 작도 문제)
• 더 복잡한 선을 그리는 작도

이를 보면, 고대 그리스 시대에도 이미 '자와 컴퍼스' 문제의 한계를 짐작을 하고 있었고, 작도 3대 고전 문제에 대한 자와 컴퍼스 작도는 불가능한 것으로 이미 받아들이고 있었다는 것을 미루어볼 수 있다.

위의 두 방법 말고도 플라톤(Plato ; BC 428-347 ), 니코메데스(Nicomedes; BC 280-220), 에라토스네테스(Eratosthenes ;BC 276-197) , 필론(BC 280 - 220 ; Philon) - 아폴로니우스(BC 262 - 190 ; Apollonius) - 헤론(AD 10 - 75 ; Heron), 디오클레스(BC 240 - 180 ; Diocles)- 스포루스(AD 240 - 300 ; Sporus) - 파푸스 (AD 290 - 350 ; Pappus) 들도 '큐빅 문제'를 해결할 방법을 제시했다. 다만 이들의 방법은 역시 자와 컴퍼스보다 복잡한 '도구'를 써서 작도하였다. 이 중 흥미로운 것은 니코메데스의 방법인데 이에 대해서는 '각의 3등분 문제'에서 보기로 한다.

보완 필요

• 앞에서 말만 하고 지나친, 고대 그리스 해법들 : 특히 니코메데스의 Quadratrix, 디오클레스의 'Cissoid' 곡선의 성질과 작도.
• 비에트(Viete ; '근과 계수와의 관계'라고 하는 것의 일반적 정리 발견 '비에트' 정리라고 함) 해법
• 데카르트 해법
• 뉴튼 해법

Note

Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia