IsoConstruction-Congruent
- 같은 넓이를 갖는 다각형들은 같은 조각들로 쪼갤 수 있다.
지금까지 우리는 정사각형을 쪼개어 조각 맞추기로 증명 와 보태서 덜어내기로 증명 에서 다각형이 면적이 같을 때, 같은 조각으로 합해지거나, 보태질 수 있다는 것을 알았다. 이 문제를 더 깊이 들어가보자. 넓이에 대한 더하기 공리는 ' 같은 조각으로 쪼개지는 두 다각형은 넓이가 같다.' 를 말한다. 과연 그것의 역도 성립할까 ? 직각삼각형의 변들로 이루어진 정사각형들을 본 것은 특수한 경우다. 이를 보다 일반화해보자. 간단히 말하면,
- 같은 넓이를 갖는 다각형은 항상 같은 조각들로 쪼갤 수 있을까?
라는 문제를 보려는 것이다. 이 문제에 대한 답은 이미 헝가리의 보야이[1](1832년)와 독일의 헤르뷘(1833년)이 독립적으로 거의 동시에 밝혔다. 두 사람 모두 전문적인 수학자는 아니었고 수학을 좋아했던 장교들이었다. 평면에서 다각형을만 보면 위의 답은 '그렇다' 이다.
- (보야이-헤르뷘 정리) : 평면에서 같은 넓이를 갖는 다각형은 항상 같은 조각들로 쪼갤 수 있다 .
이들의 증명 절차를 보면 어떻게 쪼갤 것인가에 대한 알고리듬까지 밝혀주고 있다. 이 정리를 증명하기 위해 필요한 보조적인 정리를 먼저 보자. 말을 줄이기 위해 먼저 기호 둘을 쓰기로 하겠다.
- '어떤 다각형 F와 G가 같은 넓이를 갖는다 '면, 라고 쓰겠다. 그리고,
- '어떤 다각형 F와 G가 같은 조각으로 쪼개진다'면, 라고 쓰겠다..
결국
- 은 더하기 공리에 따라 분명하고,
- 은 보야이-헤르뷘 정리로 밝혀져
이 두 '관계'는 평면의 다각형에 대해서는 등가다.
의 기초적인 성질
우선 이 새로운 관계 의 기초적인 성질을 보자.
같음(Equivalent) 관계란 수에서 '같다(=)' 나 기하학에서 '같다'(; 합동) 처럼, 그리고 이미 여러번 나왔듯이 다음의 세 관계를 만족하는 관계를 말한다.
- (Refexity) 어떤 다각형 F 에 대해서도
- (Symmetry) 어떤 두 다각형 F, G 에 대해서도 이면, .
- (Transitiveness) 어떤 세 다각형 F, G, H 에 대해서도 이고 이면, .
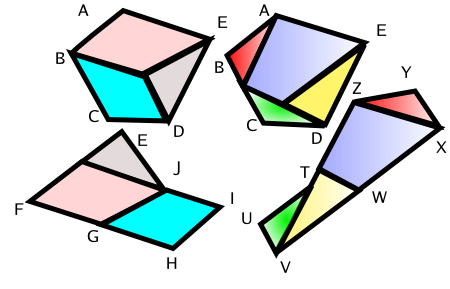
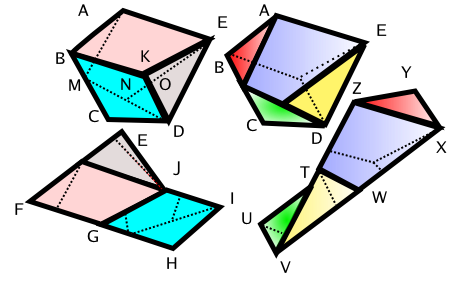
앞의 두 성질은 뻔하다. 문제는 세번째다. F 와 G 가 같은 조각으로 쪼개지고 G 와 H 가 같은 조각으로 해도, 이것이 바로 F와 G 가 같은 조각으로 쪼개진다고 보장할 수는 없다. F 와 G의 조각들과 G와 H 의 조각들이 일반적으로 같다고 말할 수 없기 때문이다. 아래 그림을 보자.
세 다각형 ABCDE , EFGHI, TUVWXYZ 을 비교해보자. 넓이가 같다고 해보자. 색깔을 잘 비교해보면, '다각형 ABCDE 다각형 EFGHI' 이고 '다각형 ABCDE 다각형 TUVWXYZ' 라는 사실을 볼 수 있다. 그렇다고 ' 다각형 TUVWXYZ 다각형 EFGHI' 라고 말하기는 아직 난처하다. 하지만 같은 조각을 더 잘게 쪼개면 문제는 달라진다. 어떻게 더 잘개 쪼개볼 수 있을까? 가장 먼저 떠오르는 방법은 역시 중간 매개인 다각형이 쪼개진 두 방식을 겹치게 하는 것이다. 위의 그림에서는 다각형 ABCED가 매개를 하는 다각형이므로 이것을 겹치면 아래 왼쪽 그림과 점선과 실선으로 표현되게 된다. 그렇다면 결국 아래 오른쪽 그림처럼 서로 같은 조각들을 공유할 수 밖에 없다.
보야이-헤르뵌 정리의 증명
어떤 다각형이든 삼각형으로 쪼개진다. 면적이 같은 두 다각형 F와 G들을 쪼개고 쪼개다보면 삼각형들로 쪼개지는 건 분명하다. 이것들이 우연히 서로 같은 모양으로 같은 갯수로 되어있다면 모를까, 일반적으로는 그렇지 않을 것이다 .아니면 조각들을 넓이는 같으면서 모양이 다른 삼각형들로 바꾼 다음 조각 모음해서 다시 삼각형을 만들 알고리듬이 있으면 증명은 쉬울 것이다. 하지만 그런 증명 전략은 난공불락의 성을 향해 무작정 덤비는 것 같다. 여기서 우리는 원과 같은 넓이인 정사각형 작도 - 고대 그리스 해법1 에서 보았듯 다각형을 삼각형 조각으로 그 다음 그것을 직각사각형으로 바꿀 수 있는 작도(알고리듬!)이 있다는 것을 떠올릴 필요가 있다.

그렇다면 이 문제를 푸는 전략을
- 어떤 삼각형도 넓이가 같기만 하다면, 같은 조각을 갖는 직각사각형으로 바꿀 수 있다는 사실
- 어떤 직각사각형도 넓이가 같기만 하다면, 같은 조각을 갖는 직각사각형으로 바꿀 수 있다는 사실
을 보이는 쪽으로 가닥을 잡는게 나을 것이다. 아래에서 더 구체적으로 보이겠지만, 이 두 사실을 확인할 수 있다면,
- 어떤 다각형 F을 삼각형으로 쪼개고 그것들을 면적이 같은 직각사각형으로 바꾼 다음,
- 바뀐 직각사각형을 다시 밑변이 같은 직각사각형으로 바꾸어 차곡차곡 쌓아 F와 같은 넓이를 갖는 직각사각형 F'을 얻고
- 그것과 넓이가 같은 다각형 G 도 마찬가지 절차를 따라 해서 G'를 얻는다.
- 다시, 넓이가 같은 두 직각사각형 F', G' 를 같은 조각으로 쪼개는 절차를 밟을 수 있다.
그렇다면 결국 앞에서 말한 Transitiveness 성질에 따라 처음 다각형 F 와 G도 같은 조각으로 쪼갤 수 있다고 믿을 수 있다. 이제 핵심적인 사실들을 하나둘 차근차근 짚어갈 때가 왔다.
삼각형을 직사각형으로
- (보조정리 1) 어떤 삼각형이든 같은 조각을 갖는 직각사각형을 찾을 수 있다.
어떤 삼각형 ABC 가 있고, 그 중 가장 큰 변이 AB 라 하자. 우리의 목표는 이 삼각형과 넓이가 같으면서 같은 조각으로 쪼개지는 직각사각형을 만드는 것이다.
- 꼭지점 C 에서 변 AB로 수직으로 내린다. 만나는 점을 D (높이의 발)라 하자. 이 때 D는 점 A 와 점 B 사이에 있을 것이다.
- 높이 CD의 중점에서 AB와 평행인 직선을 작도한다.
- 꼭지점 A에서 앞의 직선에 수직으로 그려 만나는 점을 E라 하고, 점 B 에서도 마찬가지로 해서 얻은 점을 F라 한다.
- 그렇다면 EABF가 우리가 찾던 바로 그 직각사각형이다.
두 직각사각형 끼리

- (보조정리 3) 두 직각사각형이 면적이 같으면 항상 같은 조각으로 쪼갤 수 있다.
어떤 직각사각형 ABCD 가 하자. 같은 넓이를 가지면서 다른 직각사각형 EFGH이 같은 조각으로 쪼개진다는 것을 보이려고 한다. AB 가 네 변 중 가장 큰 변이라고 가정하자.
- EF와 평행하고 G에서 H쪽으로, H를 지나는 반직선을 긋는다.
- 점 E를 중심으로 하고 AB의 길이를 반지름으로 하는 원을 그려 위에서 그은 반직선과 만나는 점 점을 L 이라 하자.
- 점 F를 중심으로 하고 AB의 길이를 반지름으로 하는 원을 그려 위에서 그은 반직선과 만나는 점 점을 K 라 하자.
- 이렇게 얻어지는 LEFK는 밑변이 EFGH와 마찬가지로 EF인 평행사변형이다.
- 한편 LEFK는 밑변이 ABCD와 마찬가지로 AB 인 평행사변형이다.

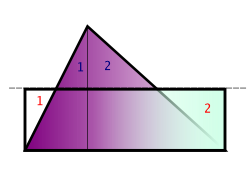
그런데, 넓이가 같고 밑변이 같은 평행사변형과 직각사각형은 같은 조각으로 이루어졌다. 오른쪽 그림을 보면 어떤 절차를 밟아 그렇게 되는지 짐작할 수 있을 것이다. 자세히 증명해보라. 아울러 더 일반적으로 다음과 같은 사실을 보일 수 있다.
- (보조정리 2) 넓이가 같고 한변의 길이가 같은 두 평행사변형은 항상 같은 조각으로 이루어져 있다.
따라서 이고 . 그래서 의 transitiveness 성질에 따라
다각형과 직각사각형
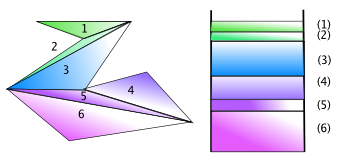
- (보조정리 4) 면적이 같은 어떤 다각형이든 같은 조각을 갖게 할 수 있다.
- 다각형 F을 삼각형 n 개로 쪼갰다고 하자. 삼각형에 1 번, 2 번, 3번, ... , n번이라고 꼬리표를 달았다고 하자.
- 1번 삼각형은 그것과 같은 조각으로 쪼개지는 직각사각형으로 바꿀 수 있다. 그 직각사각형에는 1' 라고 꼬리표를 달자. (보조정리1)
- 이 절차를 n까지 모두 한다. 우리에게는 1', 2', 3', ... n' 직각사각형이 있고, i 번 삼각형 i' 번 직각사각형이다.
- 어떤 길이 a를 정하자. 1' 번 직각사각형은 밑변이 a이면서 넓이는 같은 직각사각형 (1" 번 꼬리표를 달아주자) 을 작도할 경우 같은 조각으로 쪼갤 수 있다. 이때 i' 번 직각사각형 i" 번 직각사각형 이다.(보조정리2)
- 이 절차를 n'까지 한다. 우리에게는 모두 밑변이 a 이고 넓이는 저마다 다를 수 있는 직각사각형들이 있다. 차곡차곡 쌓으면 밑변이 a 고 면적이 다각형 F 와 같은 직각사각형 F'를 얻는다. 물론
- 다각형 G도 같은 절차를 밟아 인 직각사각형 G'를 얻는다.
- i' 번 직각사각형 i" 번 직각사각형 이기 때문에 다.
결국 다.
더 알아보기
평면에서 같은 넓이를 갖는 다각형은 항상 같은 조각들로 쪼갤 수 있다는 사실은 이제 충분히 이해할 수 있을 것이다. 여기서 머물를 수 없다. 지금까지
- 평면에서
- 다각형들의
- 쪼개기
를 다룬 셈이다. 이쯤 왔으면 자연스럽게 궁금한 게 생길 수 밖에 없다. 문제의 조건을 바꾸면 상황은 어떻게 될까? 다각형에 대한 내용이 아니라면 그것은 이미 새로운 수학의 영역으로 넘어가는 셈이라, 너무 멀리 가는 것 같다. 그건 그대로 두고, 두 개의 조건들을 풀어가보자.
다각형의 형태

다각형의 쪼개기에 대한 성질을 증명할 때 우리가 모델로 삼은 다각형들은 주로 볼록 다각형이었다. 볼록다각형이 아니거나, 하나의 (simple) 폐곡선으로된 다각형이 아니라면 어떻게 될까? 다시 말해, 다각형 구멍이 뚫린 다각형은에 대해서도 결과는 변화가 없을까?
물론 바뀔 게 없다. 증명 어디에도 구멍이 뚫리고 안뚫리고는 영향을 주지 않는다. 증명에서 다각형에 대해서 쓴 유일한 성질은 다만 그것이 삼각형들로 완전히 쪼개지느냐 아니냐 하는 것 뿐이었다.[2]
쪼개기가 아니라 보태기인 경우
피타고라스 정리를 증명할 때, 정사각형을 쪼개어 조각 맞추기로 증명 와 보태서 덜어내기로 증명 에서 살폈듯 면적이 같은 두 도형은 같은 조각만큼을 보내서 같은 도형이 나오게 게 할 수도 있다. 그렇다면 여기서 새로운 관계를 생각해 볼 수 있다.
- 어떤 다각형 F 와 G 에 같은 다각형 조각을 더해서 같은 다각형을 얻을 수 있다면 이 두 도형은 '보태서 같아지는 관계'라고 부르자.
그렇다면 보태서 같은 도형이 만들어지면 그 두 도형은 물론 넓이가 같아질 것이다. 하지만 그 역은?
- 넓이가 같은 두 다각형은 항상 같은 다각형만큼 보태서 같은 도형을 얻을 수 있을까?
이 질문에 대한 답도 앞에서 본 것과 마찬가지다. 왜냐하면 면적이 같은 두 도형이 있다하자. 그것을 완전히 싸버릴 수 있는 넓이와 형태가 같은 직각사각형이 있을 것이다. 같은 두개의 직각사각형에 처음의 두 다각형을 담았다가 빼냈다고 해보자. 그렇다면 남은 다각형도 넓이는 같다. 따라서 이것은 지금까지 보아왔듯, 같은 다각형 조각으로 쪼개진다. 따라서 같은 조각만큼 더해서 같은 도형을 얻을 수 있다. 정리해보면,
- 비교할 다각형이 A, B 라고 하자. 넓이는 같다. 이제 이것을 감쌀 같은 직각사각형을 생각해보자. 그것을 C 라 하자.
- C에서 A 를 빼내고 남은 다각형을 , B 를 빼내고 남은 다각형을 라 하자.
- 이고 따라서, .
- 따라서 A 와 B에 같은 조각만큼 더해서 같은 도형을 얻을 수 있다.
차원을 높이면 ?
공간에서는 상황이 어떨까? 문제는 조금 복잡해진다. 우선 질문을 다듬어보자.
- 3차원 공간에서 어떤 두 다면체가 같은 부피를 갖는다면 더 작은 다면체 조각들로 쪼개질까?
이 문제는 힐버트(D.Hilbert)가 제기했던 유명한 힐버트 문제들 세번째였다. 이 문제에 대한 답을 얻는데 수학계는 오래기다리지 않아도 되었다. 문제가 제기 되었던 바로 그 해 힐버트의 제자였던 덴(Max Dehn)이 반례를 들어 증명했다.여기서 다룰 문제는 아니라 공간에서의 쪼개기 에서 따로 다루겠지만, 결과만 우선 보자.
- (덴의 정리) : 3차원 공간에서 부피가 같지만 같은 조각으로 쪼갤 수 없는 다면체가 존재한다.
오늘은 여기까지.
Note