Pythagoras Th Proof2

피타고라스 정리 증명  : 보태어 덜어내기

피타고라스 정리를 증명하기 위해 '쪼개서 더하기 증명' 에서는 직각삼각형의 변 마다정사각형을 쌓고, '어떤' 규칙을 따라 조각내어 비교하였다. 그 '어떤'의 차이에 따라 다른 증명들이 탄생했고, 그 증명들은 새로운 질문을 낳았다. 이제 함께 볼 방법은 언뜻보면 사뭇 다르게 보인다. 여기서는 정사각형들을 쌓고 덧대 보탠다. 그것들 사이의 관계를 비교하면서 직각 삼각형의 변들의 관계를 보이는 보이는 방법이다.

보태어 덜어내기 증명 1 : 육각형

이것은 르네상스가 낳은 레오나르도 다 빈치가 한 증명이라고 한다. 왼쪽 그림처럼 주어진 직각삼각형 ACB 와 같은 삼각형 ECF와 HIJ 을 보태 넣는다. 이 때, 직선 CI와 직선 DG 가 직각이 된다. (확인해보라.)

마찬가지 결과가 나오지만, 다른 방식으로 쌓아 올려보자.

• 직각삼각형의 변들에 정사각형을 올린다.
• 두 점 D와 G를 잇는다. 이 직선은 C 를 지날 것이다. (진짜?)
• 두 점 E와 F를 잇는다. 이렇게 이루어진 삼각형 ECF는 원래 삼각형 ACB 와 DG에 선대칭이다. (정말?)
• 직선 DG 의 점 C 에서 직각인 직선을 작도한다.
• 직선 BC 에 평행이면서 점 J 를 지나는 직선을 작도하여 바로 위의 직선과 만나는 점을 I 라고 하자. 이때, 직선 IH 는 직선 AC와 평행이다. (왜?)

이제 작도는 끝났다. 이제 피타고라스 정리를 가볍게 증명할 수 있는 만반의 준비가 끝났다. 중심이 되는 것은 바로

S(육각형 DABGFE) = S(육각형 CAJIHB)

라는 사실이다. 육각형 중 하나를 '적당히 ' 회전하면 겹친다. (적당히란, 어느 점을 중심으로, 얼마만큼, 어느 방향으로 회전한 것일까?) 겹친 다는 사실을 믿었으면 이로부터 우리가 원하는 것을 뽑아낼 수 있다. 무엇을 말하나? 가만 귀를 기울여보면 모두 들을 수 있다.

• S(DABGFE) = S(ABC) + S(EFG) + 두 정사각형
• S(CAJIHB) = S(ABC) + S(JIH) + 큰 정사각형
• S(DABGFE) = S(CAJIHB) 이고 S(ABC) = S(EFG) = S(JIH)

다시 말해 '보태어 만들어진' 육각형에서 같은 부분 S(ABC) 만큼씩 '덜어내면' 남은 도형은 넓이가 같을 수 밖에 없다. 아름답다.

보태어 덜어내기 증명 2 : 덮기

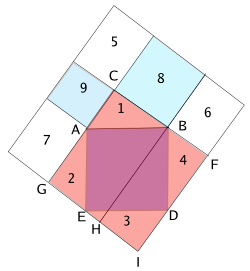
또 하나 보자. 오른쪽 그림을 보면서 가자. 처음 직각삼각형 ABC의 변들에 정사각형을 쌓았다. 거기에 오른쪽 그림과 같이 덧대어 가자. 그림을 보면 충분히 이해가 갈 것이다. 이는 처음의 직각삼각형과 쌓아놓은 정사각형들의 꼭지점과 변들을 지나며 덮어버리는 사각형을 작도한 것이다. (이때, 가장 큰 사각형은 정사각형일까, 아닐까? )

무슨 일이 있었을까? 닫혀진 막을 걷어보자. 편하게 말하기 위해, 직각사각형 BCGH 를 I 로, FBHI를 II로 부르기고 한다.

1. S(1 + 2 + 3 + 4 + 5 + 6+ 7+ 8 + 9 + 빗변으로 이룬 큰정사각형)= S(I + II + 5+ 6+ 7 + 작은 사각형 둘 8,9 )
2. S(1 + 2 + 3 + 4)= S(6 + 7),
3. S(6 + 8) = S(I) 이고 S(7 + 9) = S(II),
4. S(1 + 2 + 3 + 4 + 5 + 6+ 7+ 8 + 9 + 빗변으로 이룬 큰정사각형) = S(1 + 2 + 3 + 4)+ S(5)+ S(6 + 8)+ S(7 + 9) + S(빗변으로 이룬 큰 정사각형),
5. S(I + II + 5+ 6+ 7 + 작은 정사각형 둘 8, 9) = S(6 + 7) + S(5)+ S(I)+ S(II) + S(작은 정사각형 둘),

따라서 보탠 것에서 같은 것들을 짝맞추어 하나둘 덜어내다 보면, 결국

S(빗변으로 이룬 큰 정사각형) = S(작은 두개의 정사각형)

보태어 덜어내기 증명 3 : 안으로 접기

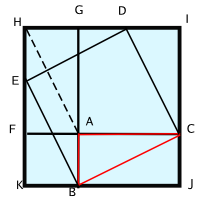
이미 ' 쪼개서 더하기 증명 ' 에서도 말했듯 어떤 직각삼각형의 변으로 정사각형을 작도하는 방법은 하나가 아니다. 지금까지 삼각형의 바깥쪽으로만 작도했지만, 꼭 그렇게 해야할 이유는 없다. 안으로 접어 보면 더 쉽게 이해되기도 한다. 오른쪽 그림을 보자.

• 직각삼각형 ABC 의 빗변을 안쪽으로 접어 넣었다.
• 직각을 이루는 두 변에서는 바깥쪽으로 내놓았다.
• 직각삼각형 ABC 와 같은 삼각형이 되도록 BJC를 보탠다.
• 변 GH 와 FK 를 연장하여 만나는 점을 작도한다.
• 그렇게 해서 새로운 큰 정사각형 HIJK 이 되도록 보탠다.

이제 여러분의 차례. 위에서 한 방법처럼, 이제 덜어내면서 비교해보라. (무엇을 어떻게 덜어내야 할까? )

기타

보태어 덜어내어 증명하는 방법은 위에서 열거된 것만 있는 것은 물론 아니다. 다른 방법들도 스스로 생각해보라. (또는 이와 비슷한 방법으로 하는 새로운 증명이 있으면 이곳에 모아주세요.)

Note

피타고라스 정리 로

Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia