Pythagoras Th Proof Euclid

피타고라스 정리 로

피타고라스 정리 증명 : 유클리드의 'Elements'

'Elements'의 증명

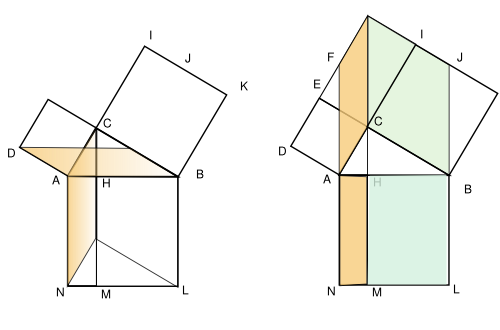
중학교 때부터 다루어왔던 방법이다. 하지만, 우리는 엄격하게 유클리드 Elements 의 논리를 따라가도록 하자. 자, 시작해보자. 주어진 것은 직각삼각형 밖에 없다. Elements I 권의 마지막에서 두번째인 정리(I권 47번 정리)을 옮겨보자.

직각삼각형에서 직각의 반대편에 있는 변을 한변으로 하는 정사각형은 직각을 이루는 두 변으로 만든 두 정사각형의 합과 같다.

옆의 그림에서 보면 분명하다. 피타고라스 정리하고 부르는 바로 그것이다.

주어진 직선에서 정사각형을 작도할 수 있다(1권 46번 정리). 따라서 그림 처럼 정사각형 셋을 작도할 수 있다.
주어진 어떤 두 점도 직선으로 이을 수 있다. (공리) 따라서 점 F 와 점 B 를 이어 선분 FB를 얻고, 점 C와 점 E 를 이어 CE를 얻는다.
주어진 직선의 점이 아닌 점을 지나면서 주어진 직선과 평행한 직선을 그을 수 있다. (1권 31) 따라서 직선 AE에 평행한 직선 CL을 잇는다.
각 ACG 는 직각으로 작도하였고, ACB는 주어진 직각삼각형에서 직각이므로 BC와 CG는 하나의 직선에 있다. 마찬가지로 AC와 CH도 한직선에 있다. (1권 14)
작도한대로 AC = FA 이고, AB = AE 이며, 각 FAB = 직각(FAC) + 각 CAB = 직각(BAE) + 각 CAB = 각 CAE 다. 따라서 삼각형 FAB 와 CAE 는 같다. 기호로 S(FAB) = S(CAE) 쓰자. (1권 4)
AC를 밑변으로하고 그와 평행한 CL에 나머지 꼭지점을 이루는 삼각형(CAE)의 넓이는 사각형 AMLE의 반이다. 마찬가지다. 삼각형 FAB 의 넓이는 사각형 GFAC의 넓이의 반이다. (1권 41)
S(AMLE의 반) = S(CAE) , S(GFAC의 반) = S(FAB) 이고 S(FAB) = S(CAE) 이므로, '같다'는 것에 대한 공준에 따라, S(AMLE) = S(GFAC) 이다. (공준)
마찬가지 방법으로 AK를 잇고 CD를 이어보면 S(HCBK) = S(BMLD).

앞의 증명은 삼각형을 썼지만, 평행사변형으로 쪼개도 된다. 직접 작도해서 해보라. 그리고 아래, 기타의 애니메이션을 참고하라.

유클리드 증명의 수정판

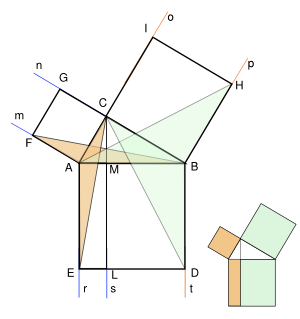
피타고라스 정리를 그림으로 보이는데 꼭 위의 그림만 써야 하는 것은 아니다. 그것은 여러가지 가능한 예 중 하나만 보였을 뿐이다. 오른쪽 그림과 같이 하면 어떨까? 직각을 이루는 한 변 중 하나를 '안쪽으로' 겹치게 해서 정사각형을 하나 작도해 보았다. 증명이 더 간단해졌다.

그렇게 작도하였기 때문에 IH 와 BC 는 평행하다.
점 C 에서 맞은 변에 수직으로 내린 선분이기 때문에 CL은 BD 와 평행하다.
따라서 빗금친 삼각형은 사각형 CIHB 넓이의 반이고, 동시에 BMLD 의 반이다.
결국 두사각형의 넓이를 비교하면, S(CIHB) = S(BMLD) 다.

유클리드는 왜 그렇게 증명했을까?

유클리드 Elements 1 권은 앞으로 기하학에서 쓰일 기초적인 성질들을 하나하나 쌓아갔다. 고대 그리스의 특징인 '엄격한 논리성'이 구현된 것이다. 이런 특징들 덕분에 고대 그리스를 수학의 태동기라고까지 일컫곤 한다. 그런데 이 1 권은 피타고라스 정리를 마지막에서 두번째인 47번 정리로, 그리고 마지막 정리는 그 역을 보이는 것으로 끝맺는다.

어떤 삼각형에서 어떤 변을 한 변으로 하는 정사각형이 다른 두 개의 변으로 이룬 두 정사각형의 합과 같으면 남은 두 변이 이루는 각은 직각이다.

마치 피타고라스 중리를 엄격하게 증명하는 것이 1 권의 목적이 아니었을까 궁금하게 만들기도 한다.

보다시피 이 증명은 논리적으로 명쾌하다. 그런데도 말도 많다. 이 증명을 비판하는 입장에서는 종종 철학자 쇼펜하우어를 인용하곤 한다. 그가 한 말의 요약은 이렇다. "이해는 하겠다. 그런데 도대체 왜 이렇게 해야한단 말인가? 왜 느닷없이 다른 것도 아니고 하필이면 그런 보조선을 그어야 했나?""우리에게는 충분히 간단하고 직관적으로 명확한 증명이 있다. 증명이라면 그래야지 왜 이리 복잡한 논리적 과정을 따라야 한단 말인가?" 그리고 마침내 그답게 "정말 놀랍도록 고약한 것 (brilliant piece of perversity)" 또는 "쥐덫 증명" 이라며 퍼부었다.^[1]

쇼펜하우어가 어떻게 비판하였든 유클리드의 증명은 깊이있고 매력적이다. 왜 그런가?

유클리드의 증명은 다른 어떤 방법보다 논리적이고 수학적이며 단순하다. 증명에서 도형들을 비교하는 것은 어떤 쪼개기나 보태기 방법보다 적다. 이 방식으로 증명하는데 쓰인 보조적인 정리는 고작 몇개 밖에 안된다. 그만큼 증명은 논리적 관점에서 '단순하다' . 그리고 보조선은 고작 셋 밖에 안된다 !
논리적으로 단순하기만 한 것이 아니다. 치밀하게 논리적이다. '어떠어떠한 공리에 따라' , '앞의 어떤 정리에 따라' , '따라서' 라는 논리적 문장밖에 없다. 앞에서 이미 말했든 기하학의 성서라 불려왔던 유클리드의 Elements 1권의 마지막 정리들은 피타고라스 정리를 끝으로 끝낸다. 공리와 공준으로부터 하나씩 하나씩 논리적이로 엄격하게 쌓아 올려 증명하였다. 여기에 필요한 직관은 처음의 공리와 공준에 대한 것일 뿐 나머지 과정은 논리의 흐름에 따를 뿐이다. ^[2] 수학의 중요한 축은 엄격한 증명이다. 그런데, 증명이란 무엇인가? 왜 증명을 해보는가? 어떤 사실 자체에 대한 논리적 설득이다. 어떤 사실이 정말 그런지 따져 본다. 하지만 거기에 머물지 않는다. 증명을 통해 우리는 '논증하는 법'을 배운다. 증명에 쓰인 개념과 논리를 터득하면서 논리적 사고를 익히게 된다. 이는 수학적 사실을 밝히는 데 머무르지 않고 사고의 논리적 결함을 없애는 훈련을 하게 한다. 더 나아가 증명의 방식에 따라 '논리적 완결성 - 미적 체험'에 이른다.
유클리드 방식으로 증명하는 동안 처음에 예상하지 않았던 흥미로운 사실까지 덤으로 알게 되었다. 꼭지점 C 에서 수직으로 내린 직선은 빗변으로 이룬 큰 정사각형을 둘로 쪼개는데, 하나는 직각을 이루는 두 사각형 중 작은 정사각형과 넓이가 같고, 다른 하나는 직각을 이루는 두 사각형 큰 정사각형과 같다는 재미있는 사실까지 알게 된 것이다.

마지막으로 하나 더, 유클리드의 보조선으로 쉽게 증명할 수 있는 방법은 '회전'이라는 개념을 적용하는 방법이다. ^[3] 그런데 왜 유클리드는 이 방법을 쓰지 않았을까? 유클리드의 Elements 에 있는 다른 정리들을 증명할때도 '변환'(꼴바꿈)의 개념을 적용하면 쉬었을텐데 그는 어쩌면 '의도적으로' 쓰지 않았다. 그 당시 기하학의 발전 수준에서 이런 방법을 몰랐을리 없다. 왜 그랬을까? 아마도 유클리드가 Elements를 쓸 때의 목적에 맞지 않았거나 실패했을 가능성이 있다. 그의 목적은 기하학의 논리적 기초를 단단하게 하는 ^[4] 것이었을 것이다. 이 목표를 위해 '정적인(static)' 성질들은 공리화가 가능했다. 그것으로부터 기하학적 사실들을 의심할 수 없는 것으로부터 하나하나 쌓아올렸다. 그런데 '자리 옮김'을 포함한 변환의 개념은 '동적인(dynamic)이 성질로, 어쩌면 이 부분을 공리화 하는데 실패했을 가능성이 있다. 이에 대해서는 토론을 필요하다. 더 깊이 탐구해들어가도 재미있겠다. 기하학의 공리에 대한 연구가 활발해지고 유클리드나 비유클리드 기하학에 대한 공리체계가 세워진 19세기 말 20세기초, 힐버트(Hilbert)의 공리체계와 같은 정적인 공리체계(Hilbert 체계) 도 있고, '자리올김'(이동)를 공리화한 동적인 체계도 있다.

더 생각해보기

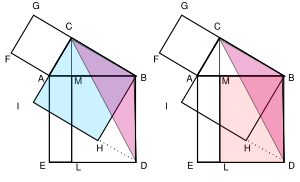
하나를 배우면 열이 궁금해지곤 한다. 그런데 그것을 정확히 문제로 포착하기는 항상 쉬운 것이 아니다. 수학은 그런 '궁금한 것이 무엇인지' 명확하게 드러나곤 한다. 이미 '쪼개기 법으로 하는 증명'에서도 새로운 문제들이 파생했듯 유클리드 증명도 새로운 문제를 제기한다. 여기 몇 개만 보인다.

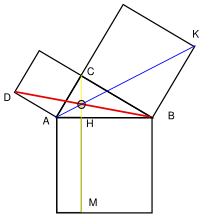
옆의 그림 보조선을 보자. 직선 BD, AK, CM 는 아래 그림에서처럼 정말로 한 점에서 만날까? 만난다면, 그 점은 삼각형 ABC 에서 어떤 점일까?
직선 BD 와 AK 는 수직일까?
안으로 접어 넣은 유클리드 증명 수정판의 그림에서 IH의 연장선은 정말로 정사각형의 꼭지점 D를 지날까?

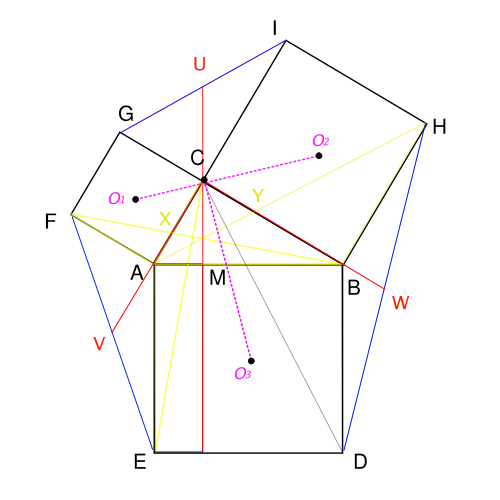
더 일반적으로... 다음 그림과 같은 풍경이 있다. 작도를 어떻게 했는지는 짐작할 수 있을 것이다. 이 풍경에서 우리는 어떤 이야기를 끌어 낼 수 있을까? ^[5]

기타

Note

↑ 참고하시길...

Although the philosopher Schpenhauer dismissed it contemptuously as a "mouse-trap proof" and "a proof walking on stilts, any, a mean, underhand proof," Sir Thomas Heath, the English editor of 'Elements', calls it "a veritable tour de force which compels admiration." It is Heath's contention that Euclid found the theorem proved by the incomplete theory of proportion of Pythagoreans (incomplete because it was not applicable to the yet undiscovered incommensurable magnitudes), and that this proof by proportion suggested to him the method of I,47. Although his plan for the 'Elements' did not call for the treatment of proportion until Book V, according the Heath theory, he managed to transform the Pythagorean proof by proportion into one based on Book 1 only. "A proof extraordinarily ingenious," insists Heath and a fig to the philosopher who expects and intuitive proof of the "look-see" type from the compiler the 'Elements' !

A Long way from Euclid, by Constance Leid, Courier Dover, 2004, p.20-21

↑ 증명 기계를 상상해보면 이 증명의 가치를 재조명해볼 수 있다. 기계는 최소한의 기초 프로그램(공리)와 논리적 틀만 입력하였을 때, 기계는 아마도 다른 어떤 방법보다 이런 방식의 증명을 해냈을 것이다. 이에 대해서는 수리논리의 발전 을 참고하기 바란다.
↑ 이에 대해서는 자리 옮김 에서 '정의' 부분을 보라.
↑ 다름아닌, 공리체계을 세우는 일
↑
이런 이야기들이 가능할까?
- $BF=CE,\ BF\perp CE$
- $CX=CY,\ CX\perp CY$
- $O_{1}O_{2}=CO_{3},\ O_{1}O_{2}\perp CO_{3}$
- U, V, W 는 GI, FE, DH 의 중점.
- 직각삼각형 대신 다른 '어떤' 도형을 작도하여 위의 그림처럼 보조선을 긋고 다른 이야기들을 끄집어 내본다면?
이 부분의 자료는 H.S.M.Coxeter, S.L.Greitzer 의 'Geometry Revisited' Ch.4. 에서 빌려왔습니다.