Arch Mech Integ

아르키메데스의 적분 개념

아르키메데스는 전시대와 동시대의 문제를 하나둘 해결해간다. 그 결과 전 시대의 미해결 문제를 해결하고 탐구의 영역을 확장했다. 이 과정에서 그 이전에는 없던 매우 독창적인 방법을 제시하기도 하고, 새로운 분야를 개척하기도 했다. 그 중 하나가, 역학적 적분법(method of mechanical integration)이다. 이는 그 이전에 그가 역학-기술자로 깊이 탐구했던 '지렛대의 원리'를 수학 분야에 대담하게 적용한 것이다. 이것은

• < 포물선의 근사 넓이(Quadrature) > 와
• <에라스토테네스에게 보낸 기계학적 정리(에포드)>

에서 사용.

포물선으로 둘러 싸인 도형의 중력중심

오늘날의 용어로 풀어 설명한다. 예를들어,

$y=ax^{2}$

으로 '둘러싸인' 부분의 넓이를 구하는 문제.

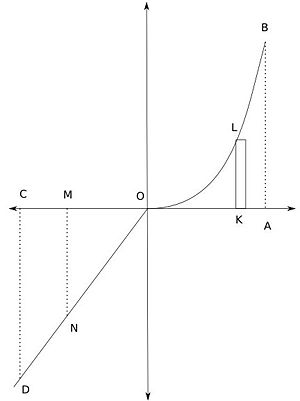
• AOC를 지렛대라고 생각해보자. 이 지렛대는 점 0 에서 균형을 이룬다고 상상한다.
• 도형의 한쪽 부분인 AOB 부분을 매우 가는 평면막대로 쪼갠다. 이 평면막대의 밑변은 $\Delta x$와 같은 표현으로 나타내기로 한다.
• OK를 x 라고 하면, KL의 길이는 $ax^{2}$ 이고, 그 평면막대의 넓이 $\Delta S=ax^{2}\cdot \Delta x$
• 이 막대를 지렛대의 끝인 A 로 옮기면, 점 O 에 대한 막대의 moment 는 $OA\cdot \Delta S=OA\cdot ax^{2}\cdot \Delta x$
• 점 O 에서 같은 길이 x 만큼 떨어진 지점인 M 에 $MN\cdot \Delta x$ 만큼의 평면막대를 걸어서 앞단계에서와 같은 moment 로 균형을 이루게 한다.
• 점 O 에 대해 양쪽의 moment들을 비교하면서, MN 값을 정확히 define 하면

$MN=a\cdot OA\cdot x$ 다. 왜냐하면

$x\cdot MN\cdot \Delta x=OA\cdot ax^{2}\cdot \Delta x$ 이니까. MN 의 길이는 x (= OK)에 비례했다.

• 이와같은 방식으로 나머지 모든 평면막대들에 대해서도 균형을 맞추도록 해줄 수 있다. 그 결과 지렛대 왼쪽은 OC 의 길이를 가질 것이다. 지렛대 왼쪽 부분의 막대들은 모두 x 에 비례하기 때문에, OND는 직선을 이루고, 그 끝에 막대의 끝이 놓인다. 그래서 그래서 끝인 CD 의 값은 $a\cdot OA\cdot OA\cdot$ 다.
• 이 과정이 모두 끝나면, A에 매우 가까운, 포물선으로 싸인 부분의 넓이 OAB 는 삼각형 OCD 의 넓이와 같아진다. 그래서,

$S={\frac {1}{2}}\cdot OA\cdot (a\cdot OA\cdot OA)$

• O 로 부터 중력 중심의 거리는

${\frac {2}{3}}\cdot OC$ 이고 따라서, ${\frac {2}{3}}\cdot OA$ .

• A 지점에 매우 가까운 지점에서 O 에 대한 넓이 S 의 moment 와 비교해보면,

${\frac {2}{3}}\cdot OA\cdot {\frac {1}{2}}\cdot a\cdot OA\cdot OA\cdot OA=S\cdot OA$

일 것이고, 따라서 결국

$S={\frac {1}{3}}\cdot a\cdot OA\cdot OA\cdot OA$.

• 이때 AB 의 길이가 $a\cdot OA\cdot OA$ 만큼인 특수한 경우에는, 포물선으로 둘러 싸인 부분의 넓이가,

$S={\frac {1}{3}}\cdot AB\cdot OA$.

이 과정은 기술자였던 경험을 반영하는 듯한 독창적인 방법이지만, 결론적으로 2차 곡선의 문제를 1차 곡선(직선) 으로 환원할 수 있다고 말한 것이다 : 2차 곡선으로 둘러싸인 부분의 넓이 문제가 삼각형의 문제로, 그래서 2차 곡선의 중력 중심 찾는 문제가 1차 곡선인 직선으로 둘러 싸인 도형(삼각형)의 중력 중심 찾는 문제로 환원되었다.

그는 어떻게 이런 '적분' 생각을 할 수 있었을까?

이런 독창적인 전개 방식을 펼치는 데에는 기술자로서의 경험과 함께, 두 사람이 영향을 준 것 같다. 데모크리토스 와 유독수스 다. 마침 아르키메데스는 이들에 대해 직접적으로 언급했다.

• <에라스토테네스에게 보낸 기계학적 정리(에포드)> 의 서문에, 피라미드와 원뿔의 부피를 구한 최초의 사람으로 데모크리토스 라고 지적했다. (그러나, 증명이 (없거나) 엄격하지 않았다고 밝혔다.)
• <구와 원기둥> 1권에서는 피라미드와 원뿔의 부피를 구하는 방법에 있어 유독수스 만 언급했다.

이에 대해 몇 개의 가설을 세울 수 있다. 먼저,

B 씨 : 연구 중 우연히 만나 보완했다

이때는 이미 플라톤 학파가 데모크리스토스의 이론을 사장시키려는 노력이 성과를 낼 때 였다. <구와 원기둥> 1권 마치고 우연히(?) 데모크리토스의 원자론적 적분 방식을 처음 알게 된다. 그리고 그 '수학적' 성과를 보고 자신에게 부족한 점이 무엇인지 알고 집중적으로 탐구해서 마침내 자신의 역학 경험과 접목했다.

D 씨 : 이미 알고 있었다

B씨, 그렇다고 말할 수 없소. 아르키메데스는 이미 <포물선의 근사 넓이(Quadrature)> 이나 <구와 원기둥> 1권 에서 증명할 때 이 방법을 쓰고 있지 않소. 내 생각엔 아르키메데스는 데모크리토스의 기하학적 원자론은 알고 있었지만, 그것이 수학적으로 엄밀성이 떨어진다고 보았던 것 같소. 그래서 그것을 중요하게 생각했던 <구와 원기둥> 에서 인용할 수 없었던 것이오.

아르키메데스가 원자론을 이미 알고 있었다는 근거를 하나 더 들어보겠습니다. <구와 원기둥> 1권, 정리 2를 봅시다. 그는 거기서 다음의 사실을 증명하지요.

" 어떤 서로 다른 두 값이 주어졌든, (큰 선분 : 작은 선분 < 큰 값 : 작은 값)의 관계가 되는, 서로 다른 두 선분이 항상 있다. "

그런데 증명 방식이 대단히 작위적이라는 생각을 하게 해요. 그냥 편하게

$A>B$ 일 때, $(A-{\frac {A-B}{2}}):B$.

를 잡으면 되는데 $A-{\frac {A-B}{2}}$ 은 A 와 B 사이의 값이고, 따라서 위의 관계가 항상 만족하는데 말이죠. 왜 이렇게 하지 않았을까요? 다는 것을 알 수 있는데 말이요. $A>B$ 일 때, $A:(B+{\frac {A-B}{2}})$ 도 있죠. 여기서 우리는 아르키메데스가, 연속성과 충돌하는 원자론의 취약점을 알고 있었던 것 같지 않소? 그렇죠? 내 생각엔 아르키메데스는 의도적으로 A-B 를 쓰지 않으려고 했어요. 원자론적 입장에서 보면, A 와 B 가 매우 매우 매우 같아서 A-B가 원자보다 더 작을 수도 있으니까요.

E 씨 : D 의 말씀이 옳습니다

저는 D 씨의 말이 맞는 것 같습니다. <구와 원기둥> 1권, 정리 4 를 봐도 그래요. 이것을 증명하는 과정에서

원뿔을 중심을 따라 쪼갰을 때 생기는 볼록한 반(半)표면은 그 끝 두 선분으로 이루는 삼각형보다 넓다.

는 사실을 증명해야했거든요. 이것을 보이기 위해 아르키메데스는,

4면체에서 서 있는 두 면의 합이 한면의 넓이보다 넓다.

라는 사실을 보이고 넘어가버리거든요. 이건, 삼각형의 두 선분이 한 변보다 길다라는 사실에서 가져온 것 같아요. 왜냐하면 높이를 따라 사면체를 '잘게 쪼개서' 삼각형들을 쌓아놓은 것처럼 하면 삼각형의 변의 길이에서 두 면이 한 면보다 넓다는 것을 유도할 수 있다고 보았을테니까요. 그렇지만, 사실, 이것은 증명없이 받아들이기는 어렵거든요.

이때 가능한 경우는 둘 중 하나라고 봐요.

• 동원한 생각(보조 정리)을 전혀 증명할 필요가 없는, 당연한 것으로 간주했거나,
• 일반적인 경우에 대해서는 성립할 수 없으므로, 그가 적용한 방법 말고는 다른 것은 있을 수 없다는 생각에, 자신이 제시한 증명을 필요로 했다.

다시 말해 아르키메데스는 자신의 결론이 완벽하지 않고 근사적인 방법으로 나타낸 것이라고 볼 수 있는 것입니다.

종합

지금까지 상황을 고려하면 이렇게 결론 지어볼 수 있다.

아르키메데스는 데모크리토스의 원자론을 미리 알고 있었지만, 수학적 엄밀함의 기준으로 봐서 그것이 타당하지 않다는 것을 알았다. 그 보다는 유독수스의 방법이 더 낫다고 보았다.

그렇다고 그가 유독수스의 방법을 그냥 따라간 것은 아니다. 유독수스는 한쪽 방향으로 '완전소모(exhaustion)'의 방법을 적용했지만, 아르키메데스는 안쪽과 바깥 쪽, 양쪽으로 적용했고, 두 둘 사이의 차이가 어떤 주어진 값보다 작을 때 비로소 그 값들이 원하는 넓이라고 증명했다. 그래서 구 표면적에 대해 지금 우리의 언어로하면,

$\int \sin {x}\,dx$

를 적용하고 있고, 회오리선의 길이/ 원의 넓이/회전체의 조각의 부피들을 구할 때도

$\int x^{2}dx,\ \int (ax^{2}+bx)\,dx$

라는, 근현대적 관점에서의 적분법 개념과 일맥 상통한 계산을 해냈던 것이다.