Doubling Cube Prove
아르키타스 해법의 증명
히포크라테스가 단순화 시킨 부분을 다시 보자. 주어진 길이 a 에 대해
인 관계가 성립하는 길이 x 를 갖는 선분을 작도하는 문제였다. 이를 위해서는
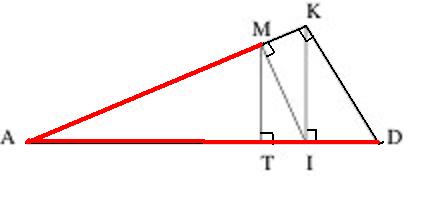
와 같이 선분 이고 이고 그 안의 삼각형들이 직각삼각형으로 닮은꼴인 도형을 작도하고,
라면 문제는 해결된다.
작도의 과정과 그림을 설명을 추가하면서 다시 보자. (추가된 설명 부분은 '진하게' 써진 부분이다.)
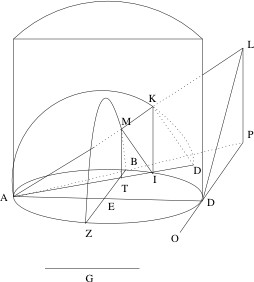
- 두 선분 AB, AD 가 주어졌다고 하자. 그리고 선분 AB가 더 짧다고 하자.
- AD를 지름으로하는 원 S 을 그린다. ( 선분 AB는 선분 AD보다 길이가 작기 때문에, AD를 지름으로 하는 원 위의 어떤 점이라고 볼 수 있다.[1] )
- AD 선분의 끝, D에 접하는 직선 o 을 그린다.
- AB를 연장하여 직선 o 과 만나는 점 P를 얻는다.
- 원 S를 밑으로하는 원기둥을 그린다.
- 선분 AP를 한변으로 하고 AD를 중심으로 회전하여 원추를 그린다.
- 원 S 를 AD를 중심으로 90도 회전하여 새로운 원 S'를 얻는다.
- 원 S'를 A를 지나는 원기둥의 직선을 중심으로 회전하여 원고리를 얻는다. ( 이 원고리는 가운데가 '점으로 뚫린(?)' 모양으로 원고리 바깥쪽 전체를 보면 반지름이 AD인 원모양일 것이다. )
- 원기둥과 원추와 원고리가 만나는 점 중 하나를 K로 얻는다. (원고리와 원추가 만나 '선'을 이룰 것이고 이 선과 원기둥과 만나는 점 중 하나를 K라 놓는다. )
- 점 K에서 원 S로 투사(projection)하여 만나는 점 I을 얻는다. ( K에서 원기둥을 따라 수직으로 내린다. )
- 선분 AD에 수직이고 B를 지나는 직선을 그어 원 S와 만나는 점 Z를 얻는다.
- 선분 BZ로부터 수직인 직선을 그어 (projection) 직선 AK와 만나는 점 M를 얻는다.( 'BZ를 원기둥의 중심을 따라 평행이동하면서 원추와 만나는 점' 이라 할 수 있다.)
- AI의 연장선이고 AD와 길이가 같은 점 D'를 얻는다.
- 점 M를 선분 BZ에 투사하여 점 T을 얻는다.
- 결과적으로 우리는 위에서 목표로 햇던 도형을 작도한 것이다.
- 다음을 주목하라
- MI과 KD'는 평행하다.
- MT와 KI는 평행하다.
- 각 AMI , 각 AKD', 각 MTA, 각 KIA는 모두 직각이다.
- 비례 관계에 따라
- |AM| : |AI| = |AI| : |AK| = |AK| : |AD'|
- 이므로 가정
- 따라서
주어진 두 선분 AB, AD 로부터 히포크라테스가 단순화시킨 문제의 해 x (여기서는 선분 AI)를 작도한 것이다.
- Doubling_Cube 로 돌아가기.
Note
- ↑ 선분 AD 위에 A와 D가 아닌 어떤 점을 B라 하고, 원 S를 작도 한 다음, 반지름을 AB로 하는 원을 작도하여 교차하는 점 중 하나를 선택하면 된다.
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia