Trisection
각의 삼등분 작도의 고전-근대의 해법
작도 가능의 기초에서 보았듯 주어진 각을 둘로 나누는 경우는 어렵지 않게 작도할 수 있다. 따라서 인 각은 모두 작도할 수 있다.[1] 또, 어떤 각이 주어졌을 때 직선과 원만 작도하여 그 각을 삼등분할 수 있을까? 라는 각의 삼등분 문제는 특별한 경우에는 작도 가능하다. 주어진 각이 90도라고 하자. 각이 주어졌다는 것은 세 점 A, B, C가 주어졌다고 볼 수 있다. (만나는 점이 A 고 |AB| < |AC|하자) 그렇다면
- 90도 각의 삼등분을 직선과 원으로 작도한다는 것은, 자와 컴퍼스만 써서 주어진 AB, AC 로 결정되는 각에서 30도를 가리키는 두 점을 찾으면 된다.
- 중심이 A고 반지름이 |AC|인 원 S 을 그려 반직선 AB과 만나는 점 B'를 얻는다. 따라서 |AB'| = |AC|
- 중심이 C고 반지름이 |AC|인 원 S'을 그려 S와 S'가 만나는 점 D를 얻는다.
- 중심이 B'고 반지름이 |AC|인 원 S'을 그려 S와 S'가 만나는 점 E를 얻는다.
- A, B', C, D, E에 따라 세각이 정의되고 우리가 찾고자 하는 두 점은 D, E다.
그런데도 고대 그리스시대에 이미, 주어진 모든 각에 대해 자와 컴퍼스로 3등분 하는 것은 작도할 수 없는 것으로 여겼다고 전해진다. 자연계에 어떤 숨은 뜻이 있어 3등분 문제는 직선과 원으로 작도가능하지 않을까? [2]
여기서는 '풀릴 수 없음' 보다는 고대 그리스 시대 부터 근대까지 '다른 도구를 써서 각의 삼등분 문제를 풀어내기' 위해 어떤 도구와 개념이 쓰이고 있는지 살펴보기로 하자. 지금부터 어떤 각이 주어졌든 항상 90도 보다 작다고 가정한다. 그것으로 충분하다 : 주어진 어떤 각 30도는 작도 가능하다는 것은 앞에서 이미 보았다. 따라서, 어떤 각 가 주어지고 90도 보다 클 경우, 을 작도 가능하면 도 작도가능하고 그 역도 참이기 때문이다.
고대 그리스의 해법 1 : 아르키메데스 해법
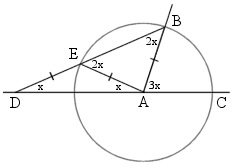
수학사에 빛나는 위대한 아르키메데스(Archimedes ; 287 BC - 212 BC)[3]는 역시 명성에 걸맞게 놀라우리만큼 간단한 도구를 써서 작도한다. 아르키메데스가 쓴 도구는 자와 컴퍼스 밖에 없다. 그러나 여기서 자는 주어진 두 점을 직선으로 잇기만 한 것이 아니라, 각을 결정하는 선분의 길이(반지름)만큼 자에 두 점이 표시된 자 또는 더 간단히 어떤 두 점을 표시할 수 있는 자 다. 표준적인 작도 가능보다 기능을 눈에 띄게 확장한 것은 없는 것 처럼 보인다. 그런데도 표준적인 자와 컴퍼스로는 풀 수 없는 문제가 이런 간단한 기능의 자로 대체하면 풀린다.[4] 여기서는 자에 |AB |의 길이 만큼의 두 점이 표시되었다고 하자.
- 어떤 각이 A, B, C 세 점으로 정의 되었다고 하자. 편리를 위해 |AB | = |AC| 라고 가정하자.
- 점 A를 중심으로 반지름 |AB | 인 원을 작도한다.
- AC를 연장하여 직선 AC 을 얻는다.
- 두 점이 찍힌 자가 B를 지나게 하고 표시된 두 점이 원에 하나, 직선 AC 에 하나 오도록 움직인다. 이 점을 D라 하자.
- 각 BDC가 찾던 각이다. 증명을 위해서는 선분 BD와 원이 만나는 점에 E를 얻고 점 E와 A를 잇고, 점 B 와 A를 이으면 된다 (오른쪽 그림 참조)
어떤 대수적 계산도, 특수한 곡선도 없이 간단하게 각의 삼등분 문제를 해결했다 !
고대 그리스의 해법 2 : Nicomedes-Pappus 해법
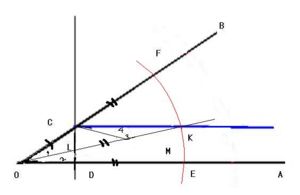
니코메데스 (Nicomedes ; 280 BC - 210 BC)는 작도 가능 문제를 푸는 과정에서 특수한 개념의 곡선을 생각하고 그것을 구현할 도구를 생각해내었다. 그 새로운 도구를 써서 각의 삼등분 문제를 해결한다. 그리고 파푸스(Pappus ; AD 290 - 350 )는 쌍곡선과 원의 교점을 찾는 방식으로 해결한다. 이것은 니코메데스가 생각해낸 도구와 논리적인 관점에서는 다를 것이 없다. 찬찬히 보도록 하자.
- 주어진 각이 세 점 O, A, B고 O가 만나는 점으로 정의된다고 하자.
- 점 O와 점 B 사이에 어떤 점 C를 얻는다.
- 점 C에서 반직선 OA에 수직인 선을 내려(projection) 만나는 점 D 를 얻는다.
- |OC|가 a라고 할 때, 반직선 OA에 C'에서길이가 2a가 되는 점 E 를 얻는다.
- 마찬가지로 반직선 OB에 점 D에서 길이 2a가 되는 점 F를 얻는다.
- 반직선 OA에 평행하고 점 C를 지나는 직선을 그린다.
- 이 평행한 직선에 어떤 점 K를 찾아 점 O에서 K를 이었을 때 그 반직선이 직선 CD와 만나는 점 L 에서 K까지의 길이가 2a되는 바로 그런 K를 얻을 수 있다고 하자.
- 각 KOA는 주어진 각 BOA의 삼등분이라는 것을 증명할 수 있다 : 점 L과 K 의 중앙을 작도하여 M을 얻는 것으로 쉽게 볼 수 있다.
이 작도 과정에서 다른 건 모두 자와 컴퍼스를 써서 작도할 수 있는데 진하게 써진 부분이 문제다. 이 문제를 해결하기 위해서는 다음의 문장이 참이면 된다.
- (끼워넣기) 정해진 길이 x와 점 O가 주어지고 주어진 두 직선 각 직각일 때, 점 O 에서 두 직선 을 교차하도록 직선을 만들면 교차하는 두 점 를 잇는 선분의 길이가 x 이게 작도 할 수 있다. [5]
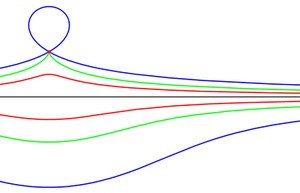
이 문제를 해결하기 위해서는 주어진 점 O에서 직선 을 따라 돌면서 O로부터 그어진 직선에 만나는 점부터 주어진 길이 x가 되는 점들만 찍으면 된다. 니코메데스가 낸 것으로 알려진 특별한 곡선의 개념이 콘코이드( Conchoid)다. [6] 콘코이드는 어떤 직선 과 점 O 과 어떤 길이 x가 주어졌을 때, 점 O로 부터 직선으로 반직선 을 그려가면서 만나는 점들마다 주어진 직선의 양쪽으로 정해진 길이 x만큼 되는 점을 에 표시해 가면 된다. 콘코이드가 '끼워넣기'를 해결하는 특수한 곡선이라는 것은 분명하다.
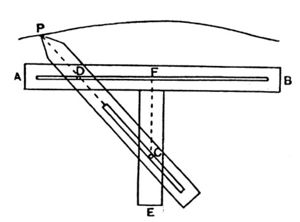
그렇다면 이것을 현실에서 유사하게 구현할 도구는 없을까? 니코메데스는 그 도구로 오른쪽 그림을 제안했다.
따라서 각의 삼등분을 작도할 때, '콘코이드를 작도할 수 있다면'
- 직선 CD와 정해진 점 O, 주어진 길이가 2a인 콘코이드를 작도하고
- 얻어진 콘코이드와 C 를 지나고 반직선 OA에 평행한 직선과 만나는 점을 K를 표시한다.
위 두 과정으로 충분히 작도 가능하다. 그렇다면 남은 질문은 이런 특수한 형태의 작도를 표준적인 자와 컴퍼스로도 가능할까? 자에 두 점을 찍을 수 있다면 가능할테지만, 아무것도 표시할 수 없고 단지 직선만 그릴 수 있는 우리의 자로 과연 ?
중세, 근대의 해법
앞에서 말했듯, 인도 아랍으로 수학의 중심이 넘어 갔다가 유럽으로 돌아오면서 기하학이 대수적 성격을 띄게 되었다. 11세기 사마르칸드의 알 까쉬가 각의 삼등분 문제는 삼차방정식으로 표현된다는 것이 밝혔다. 보통 삼각법을 써서 나타내는 것이 일반적이지만, 이는 15세기 이후의 일이다. 그 이후 수백년이 지나 데카르트는 알-까쉬의 방법보다 훨씬 간단하게 삼차 방정식으로 각의 삼등분 문제를 나타낼 수 있음을 보였다. 이 두 결과는 모두 삼각함수법을 쓰지 않고 기하학적인 사고를 대수적으로 표현한 것이다. 삼각함수 개념을 써서 나타낸 방법을 참고삼아 보자.
-
- 이므로 어떤 각 3x 가 주어졌다면 이는 상수 라고 할 수 있고, 따라서 우리가 찾고자 하는 각 x 의 사인함수값을 변수 y로 하는 식을 만들면
의 문제로 삼차 방정식 문제로 귀결한다. 이런 3차 방정식의 근이 되는 선분의 길이를 자와 컴퍼스로 작도할 수는 없다. 이에 대해서는 작도 불가능성 부분에서 이어진다.
그 이후 각의 삼등분 문제를 자와 컴퍼스가 아닌 다른 도구를 써서 발견한 결과를 열거해보자.
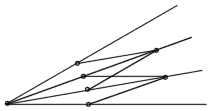
- 16세기 : 데카르트 해법 (특수 도구 사용 : 옆 그림 )
- 17세기 : 앙뜨완 파스칼[7]의 달팽이 곡선 사용 해법
- 17-18세기 : 죠바니 체바의 해법
보완할 것들
- 끼워 넣기 방법에 대한 일반적인 이야기를 더 자세하게 하고 콘코이드 해법이나 다른 방법을 '작도'의 개념으로 분명하게 설명하기.
- 콘코이드 그래프의 '함수적 표현'
- 콘코이드 해법과 쌍곡선 원의 교점의 등가성 : 파푸스
- 고대 그리스의 Neusis 작도 : 종이 접기 포함
- 고대 Qudratrix 이용한 해법
- 중세 - 근대 해법 상세히
- 특수 곡선 (Conchoid, Quadratrix ...) 들의 현대적 응용
- Trisectrix
- 삼각형의 '삼등분선'의 성질들
- 모를리 정리 : 주어진 어떤 삼각형의 각의 삼등분선의 교점들로 된 삼각형은 정삼각형이다.
- 다른 재미있는 성질들?
Note
- ↑ 고전적인 작도 가능문제의 중요한 부분이었던 정다각형 작도 문제에 대해 간단히 말하고자 한다. 정 3 각형과 정 4 각형, 정 5 각형이 자와 컴퍼스로 작도할 수 있다는 것은 이미 유클리드 원론 시대에도 알려졌다. 그리고 각을 이등분할 수 있으니 정 6, 8, 10 각형도 작도 가능하다. 그러나 소수인 7 각형이나 17 각형 같은 경우는 문제거리였다. 18 세기 끝자락에 이르러서야 가우스가 가우스가 17각형 작도 가능 을 밝혀냈다. 이후 일반화된 형태로 풀어낸 것처럼(가우스가 가설로 냈지만, 완전한 증명은 완쩰이 해냈다. 완쩰에 대한 이름은 작도 가능 부분에서 앞으로 여러번 나올 것이다.)
- 정 m 각형을 자와 컴퍼스로 작도가능하다면 m 은 꼴이고 그 역도 성립한다.
- ↑ 정말 궁금하다. 그리고 고대 그리스 사람들이 설령 증명은 하지 않았다고 해도 어떤 '추론'을 통해 이것이 불가능하다는 짐작을 했던 것일까? 보완필요.
- ↑ 플루타르크가 전하는 이야기에 따르면, 아르키메데스는 황족으로 발명과 수학계산에 초인적인 능력을 발휘하였다. 어느날 황제에게 편지를 써서 힘을 거의 안들이고 엄청 무거운 물건을 들거나 끌 수 있다고 전했다. 흥미를 가진 황제는 그에게 큰배에 사람과 물건을 가득 실어 끌어들이게 했는데, 손동작 하나로 배를 끌어들였다고 한다. 또한 그는 받칠곳만 있다면 지렛대를 이용해서 지구도 들어올릴 수 있다고도 호언하였다. 강력한 로마군이 당시 가장 이름을 떨치던 장군의 지휘로 쳐들어 왔을 때, 그가 발명한 도구로 물리친다. 그는 이미 근대 해석학의 기초개념을 직관적인 형태로 이해하면서 쓰고 있었고 그것을 통해 수많은 수학적 진실을 밝혀냈다. 그 중에서도 그가 가장 자랑스러워 하는 것은 '원추의 부피'를 구한 식이라고 한다. 아르키메데스의 저서들은 여러권이 지금까지 전하고 있다.
- ↑ 하지만 우리가 생각하기에 '간단해보이는' 그 기능은 '끼워넣기'라는 기초적으로 매우 중요한 기능을 담고 있다. 정해진 길이만큼의 길이를 '끼워넣기'할 수 있다면 작도 가능문제의 영역은 눈에 띄게 바뀐다. 이와 연관된 예가 앞으로 더 나올 것이다.
- ↑ 이와 연관된 질문 둘.
- 직각이란 조건을 빼면 어떻게 될까?
- 이 문제를 파푸스는 '쌍곡선과 원의 교점'의 문제로 바꾸어 두 작도가 모두 같은 결과를 낸다는 것을 보였다. 어떻게?
- ↑ 로마어 권인 영어로 Conchoid라고 하고 '콘호이드'라고 하기도 한다.
- 에 가면 예를 볼 수 있다 이 사이트에서는 주어진 점 O 와 직선의 길이 보다 정해진 길이 x가 더 긴 경우의 특수한 예다.
- 만약 주어진 점 O 와 직선의 길이가 x 와 같다면, 또는 크다면 어떻게 그려질까?
- mathworld 설명 극좌표(polar) 시스템에 그린 그림들.
- 설명과 예쁜 그림들
- ↑ 유명한 블레즈 파스칼의 아버지
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia















