Geom Construction MoreLess: 두 판 사이의 차이
(차이 없음)
|
2009년 4월 22일 (수) 13:38 기준 최신판
작도 가능의 축소와 확대
이미 작도 가능 문제(총론) 에서 표준적인 작도 가능의 뜻은 어느정도 정의를 했다. 그렇다면 이 표준을 바꾸면 어떻게 될까? 작도 가능의 정의에서 등장한 조건들을 '확대하거나 축소한' 가정이나 조건으로 작도한다면 그 결과는 어떻게 될까? 먼저, 작도 가능 문제를 정의할 때 등장한 조건들을 라는 문장들을 나열해보자.[1] 정의에 따르면
- 주어진 유한개 점의 집합으로부터
- 분명히 정해진 기능을 하는 도구를 사용하여 작도하면서 (표준적으로는 '자와 컴퍼스')
- 단계마다 새로운 점을 추가하면서 (앞서 작도한 직선과 원들의 교점, 또는 그 위의 임의의 점)
- 유한번 단계를 거쳐
- 마침내 목표로 하는 유한개 점들을 찾아낸다.
여기에 드러내지는 않았지만 암묵적으로 가정하고 있는 아래 부분을 추가하자.
- 어떤 두 점을 지나 직선을 작도하는 자는 끝없이 연장할 수 있다.
- 작도하는 평면은 끝이 없다.
이상적인 자와 종이를 현실적인 자와 종이로 : ()
가정 는 현실적으로 가능하지 않다. 그래서 마음 속에서 상상의 작도를 한 셈이다. 예를 들어 어떤 네 점 A, B, C, D 가 있다고 할 때, ( )
- (이상적인) 자로 A와 B 를 잇는 직선 AB 과, C와 D를 잇는 직선을 작도한다. ( )
- 이 두 직선 AB , CD 가 평행하지 않다면 항상 교점 E 를 얻을 수 있다. ()
라는 사실은 우리가 했던 가정에 따르면 당연해보인다. 그런데 현실적으로는 끝없이 연장할 수 있는 자도 없고 그것을 그릴 평면도 끝없이 넓을 수 없다. 그 가정들을 축소해서 다음과 같이 더 현실적으로 바꾸었다고 하자.
- 정해진 길이 a 보다 작은 거리에 있는 어떤 두 점이 있다면 이를 잇는 직선을 작도할 수 있다. 다시 말해 자의 길이가 a로 정해졌다고 하자.
- 우리의 평면은 끝이 있다. 다시 말해 공책 크기 종이에 작도를 한다고 하자.
앞의 예에서 새로 얻을' 점 E 는 새롭게 가정한 우리의 평면 밖에 위치할 수 있다. 그리고 점 A 와 B 사이의 거리가 a 보다 클 수도 있다. 그래서 AB, CD 를 연장해서 점 E 를 작도할 수 있을까? 물론 작도할 수 없다. 연장하면 있겠구나 짐작할 수는 있지만 그것을 '눈에 보이게' 나타낼 수는 없어 보인다. 그렇다고 이것이 '작도 가능'이 본질적으로 축소되었다고 할 수는 없다. 왜냐하면, 첫째, 작도가능이란 눈으로 직접 보이는 것이 아니라, 그 점을 찾을 수 있는 방법(알고리듬)을 구체적으로 드러내어 그 방법에 따라 찾을 수 있다는 것이 의심할 수 없으면(그 점이 문제의 조건을 충족한다고 증명하면) 그것으로 충분하기 때문이다. 결론적으로, 모든 의미있는 작도 가능한 기하학적 문제는 현실적인 자와 평면에서도 작도 가능하다. 어떻게 그것을 보일까?
어떤 거리로 제한된 자
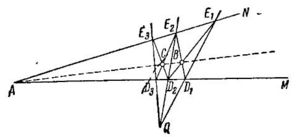
어떤 자의 길이가 제한되어 있다 하더라도 표준적이고 이상적인 자를 썼을 때와 견주어보아도 작도 가능이 본질적으로 축소되지는 않는다. 정말 그럴까? 여기에 쓰이는 정리는 다음과 같다. (스스로 증명해보라.)
- 정리 : 각 MAN 과 그 반직선에 없는 점 Q가 주어졌다하자. 점 Q을 지나는 세 직선을 그어 만나는 점을 와 라 하자. 그럴 때, 와 의 교점을 B라 하고 와 의 교점을 C라 하면, 점 A, B, C는 한 직선에 속한다. (오른쪽 그림)
그러면 다음 사실을 보일 수 있다.
- 어떤 두 점 A, B의 거리가 주어진 자의 길이 a 보다 크다고 해도 직선 AB를 작도할 수 있다.
- 자를 반복해서 써서(어떻게 작도할까?), 점 B 에 '충분히 가까이' 있고 A 를 지나는 직선 를 작도한다. 여기서 주어진 길이의 선분을 연장하는 작도는 컴퍼스만 써도 된다. 오른쪽 그림에서처럼 선분 a 를 결정하는 두 점이 O 와 A 라 하고 이를 컴퍼스만 써서 연장해보자.
- 점 O 에서 A로 원을 작도 하고 점 A에서 |OA|를 반지름으로 하는 원을 작도하여 만나는 점을 P라 한다.
- 점 P를 중심으로 하고 마찬가지 방법으로 원을 작도하여 점 Q를 얻는다.
- 점 Q를 중심으로 하고 마찬가지 방법으로 원을 작도하여 점 C를 얻는다.
- 이때 선분 AC는 선분 AO의 두배가 되고 하나의 직선위에 있는 점이다. 이 과정을 반복한다.
- 점 B 를 지나는 서로 다른 두 선분 을 작도하여, 선분 들이 직선 과 만나는 점을 로 하고 직선 과 만나는 점을 로 한다.
- 선분 와 의 교점을 Q라 한다.
- 점 Q를 지나는 직선을 그어 직선 과 만나는 점을, 직선 와의 교점을 로 한다.
- 선분 와 의 교점을 C라 한다.
- 그럴 때, 점 A, B, C 는 한 직선에 있다. 따라서 B와 C를 잇는 직선이 우리가 찾던 직선이다.
제한된 평면
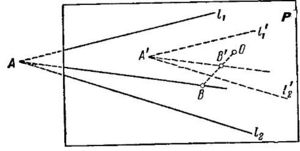
처음부터 암묵적으로 끝없이 펼쳐지는 평면이라고 가정했지만, 실제로 작도하는 평면이 A4 용지처럼 어떤 크기의 평평한 종이라고 해보자. 이 현실적인 평면을 평면을 P 라 하자. 이제 이 평면 P 에 있는 어떤 점 B 에서 이 평면 '밖에' 있는 점 A 로 직선을 작도할 수 있다는 사실만 보이면 충분하다. 방법은 최소한 두가지다.
- (방법 1) 앞의 '자의 제한'에서 처럼 A, B의 직선을 앞의 작도에서 BC 직선과 같으므로 마찬가지 방법으로 하면 된다.
- (방법 2) 축소된 닮음 변환을 씀
- 점 B 에 '충분히 가까이' 있고 A 를 지날 직선 를 작도한다.
- 평면 P 에 축소할 때, 축소하는 정도를 알 수 있는 기준이 되는 점 O를 찍어 O 에서 축소 닮음 변환을 한다. 직선 는 로 '짧고 평행하게' 옮겨지고 점 B는 B'에 대응한다.
- 직선 이 만나는 점을 A'로 놓는다.( 직선 A'B'는 AB 에 평행하다)
- 직선 A'B'에 평행하고 점 B를 지나는 직선을 작도하면 이 직선이 작도하고자 했던 직선이다.
축소된 평면에서 얻은 직선은 그것을 연장하면 결국 무한히 뻗어 있는 평면에서 두 점을 잇는 것과 다를바 없다. 위와 같이 평면 전체를 축소해야할 경우 뿐만 아니라, 평면에 구멍이 뚫려 있어서 두 점사이를 직접 이을 수 없는 경우도 앞에서 했던 축소 닮음 방법으로 방법으로 극복할 수 있다. A 지점에서 B 지점으로 직선을 측량하는데 그 중간에 산이 가로 막고 있거나 연못이 놓여 있을 경우를 상상해보라.
무한개의 점이 주어질 수 있다면 ( )
유한 개의 점이 주어진 것이 아니라 무한 점이 주어질 수 있다면 어떻게 될까? 예를 들어 주어진 점들의 집합을 좌표축에서
라고 한다면 우리가 풀 수 있는 문제는 근본적으로 확장할 수 있을까? 이 경우는 작도 가능의 범위가 본질적으로 확장된다. 예를들어 위의 집합이 주어졌다고 하자.(설명의 편리를 위해 좌표를 알 수 있다고 하자) 그렇다면 x 좌표를 이루는 직선에 평행하고 거리가 2 만큼 떨어진 직선
를 자와 컴퍼스로 작도하고 원래 주어진 점들의 집합과 새로 만들어진 도형의 교점()으로 '어떤 큐빅의 두 배인 부피의 큐빅'의 한변의 길이의 예가 되는 선분 을 작도할 수 있게 된다.
질문 : 무한 개의 점이 주어질수 있다는 가정을 하면 대표적인 작도 문제인 각의 삼등분, 원의 면적과 같은 정사각형 작도하기와 그 역, 정 다각형의 작도 문제들을 풀 수 있을까? 작도할 수 있는 경우, 어떤 무한점들을 가정하면 될까? 다양한 예를 찾아보시오.
자와 컴퍼스의 가정을 바꾼다면 ( )
원래 표준적인 정의에서는 '이상적인 자와 컴퍼스'를 쓰고 있는데 이의 가정을 바꾸어, 자만 쓰거나, 컴퍼스만 쓰거나, 자에 눈금이 표시된 자를 쓰거나, 직각을 작도할 수 있는 자를 쓰거나, 아니면 자와 컴퍼스보다 더 복잡한 도구를 써서 작도한다면 그때 는 근본적으로 축소되거나 확장될까?
컴퍼스만 쓸 경우
작도 가능의 기초 첫부분 예제를 다시보라. 여기서 주어진 문제에 대해 두가지 작도 알고리듬을 제시했다. 이 두가지의 방법의 근본적인 차이는 하나는 직선을 그릴 수 있는 '자'를 쓸 수 있었다는 것이다. 이 직선 위에 있는 점들에 대해 '직선 위에 있다(collinear)' 하다는 것은 굳이 밝히지 않았도 되었다. 하지만, 두번째 방법은 자 없이 컴퍼스만으로 작도한 것이라, 원을 여러개 그려 서로 만나는 점들을 얻었다고 해도, 그 새로 얻은 점들이 '정말로 한 직선 위에 있는지' 밝혀주어야 했다. 이처럼 자와 컴퍼스로 작도할 수 있는 문제를 컴퍼스만 써서 작도할 경우 그 알고리듬도 복잡해지고 증명은 더 까다로와 질 수 밖에 없다.
- 예제 1: 직선 AB 와 어떤 점 C 를 중심으로 하는 원의 두 점에서 교차한다고 하자. 두 교차점을 작도하라. 점 C 를 중심으로 하는 원의 반지름을 r 이라 하자.
- 자와 컴퍼스가 모두 있을 때는 이것은 '공리'인 셈이다. 하지만, 컴퍼스만 있다고 할 때 이 문제는 벌써 공리가 아니고 증명해야한다. 다음의 알고리듬이 가능하다.
- 점 A 를 중심으로 하고 점 C 까지를 반지름으로 하는 원을 작도
- 점 B 를 중심으로 하고 점 C 까지를 반지름으로 하는 원을 작도
- 두 원의 교점 중 C 가 아닌 점을 C' 라 하자. C 에서 r 을 반지름으로 하는 원을 작도하고 C '에서도 마찬가지.
- 이 때 만나는 두 점이 D 와 E 다.
- 이 문제의 증명의 핵심은 위의 알고리듬으로 얻은 두 점 D, E 가 정말로 A, B 와 collinear 하냐는 것을 보이는 데 있다. CC'는 직선 AB 와 직각이고 동시에 직선 DE 와도 직각이다. 따라서 두 직선 AB 와 DE 는 평행하거나 겹친다. 그런데 C , C' 에서 A 또는 B 까지 떨어진 거리는 r 로 같다.
- 그런데 여기서 C 가 아무데나 가능한가 ? 만약 C 가 A 와 겹친다면?
- 예제 2 : 주어진 두 선분 AB 와 DE 가 있다고 하자. 그리고 점 C 가 점 A와 B 사이를 m : n 으로 나눈다고 하자. 그럴 때, 두 점 D 와 E 사이에도 m : n 으로 나누는 점 F 를 찾을 수 있다. 컴퍼스 만 써서 작도해보라.
- 점 D 와 점 E 를 중심으로 하고 반지름을 AB 로 하는 두 원을 그려 교차점을 얻는다. 이 점 중 하나를 G 라 하자.
- 점 G 에서 BC 를 반지름으로 하는 원을, 점 D 에서 AC를 반지름으로 하는 원을 작도. 만나는 한점을 H 라 하자.
- 점 D와 H 에서 AC 를 반지름으로 하는 원을 그려 만나 새로 얻은 점이 바로 F 다.
- 여기서도 마찬가지로 DFE가 collinear 하다는 사실과, 문제의 비례 관계가 성립한다는 사실을 모두 보여야 한다. 스스로 보여보라. (넌지시: GDE와 HDF는 닮은 꼴의 삼각형을 이룬다. ) 이 알고리듬을 잘 보라. 이 작도 알고리듬으로 하면 선분 AB 의 길이가 아주 작을 경우 이런 작도는 언뜻 봐서는 도움이 안된다. 정말 그런가? (그렇지 않다. 우리는 주어진 선분을 얼마든지 '늘릴' 수 있다. 주어진 선분 AB 가 충분히 크다고 가정해도 된다. )
놀랍게도, 컴퍼스만 쓸 경우도 자와 컴퍼스를 쓰는 것과 본질적으로 차이가 없다고 밝혀졌다. 이 사실은 17세기 중반 덴마크의 모어(Mohr) [2]와 이탈리아의 마스케로니(Mascheroni) [3]가 100년 정도의 시차를 두고 독립적으로 증명하여 모어-마스케로니 정리로 알려졌다.
- 모어-마스케로니 정리 : 자와 컴퍼스로 작도 가능한 모든 문제는 컴퍼스만으로 작도가능하다.
물론 이 사실이 '직선을 컴퍼스로 그릴 수 있다'는 것을 뜻하지 않는다. 처음에 정의할 때, 직선은 두 점으로 정의된다고 하였으므로, 모어-마스케로니 정리는 직선을 이룰 수 있는 두 점을 자와 컴퍼스로 작도할 수 있을 경우, 반드시 컴퍼스만으로도 작도할 수 있다는 것을 뜻한다. [4] 이 정리를 확신하는데 필요한 핵심은, 물론
- 직선과 직선의 교점, 직선과 원의 교점을 컴퍼스만을 써서 작도할수 있나 ?
에 따라 결정된다. 어떻게 할까?
다음의 과정을 밟아 이를 증명할 수 있다.작도에는 컴퍼스만 사용하므로 아래 작도는 모두 '컴퍼스 작도가능'이라는 점을 환기하라.
- 선대칭 : 세 점 A, B, C 가 주어졌다. 그럴 때, 점 C 가 직선 AB 에 '대칭(symmetry)'하는 점을 작도할 수 있다.
- 점의 뒤집기 원 과 점 A가 주어졌다. 그럴 때 점 A의 뒤집힌(inversion) 점을 작도할 수 있다. [5]
- 직선의 뒤집기 : 원 과 점 A, B 가 주어졌다. 그럴 때 직선 AB의 뒤집힌 원을 작도할 수 있다.
- 점 O가 직선 AB에 대칭한 점 O'를 작도한다.
- 점 O'를 원 에 대해 inversion한다.
- 세점을 지나는 원 작도 : 세 점 A, B, C가 주어졌다. 그럴 때 세 점 A, B, C를 지나는 원을 작도할 수 있다.
- 중심을 A로 하는 원을 작도하여 그 원에 대하여 B 를 inversion하여 B'를 얻고, C를 inversion하여 C'를 얻는다.
- 직선 B'C'을 위의 원에 inversion한다.
- 원과 직선의 교점 작도 : 원 과 두 점 A, B가 주어졌다. 그럴 때 그 원과 직선 AB의 교점 C,D가 있다면 이를 작도할 수 있다.
- 직선 AB를 원 에 inversion하여 원을 얻는다.
- inversion 변환 후 직선의 점 A와 B는 원의 점 A' , B'로 바뀌지만, 교점 C, D는 inversion해도 교점으로 그대로 C, D로 남는다.
- 직선과 직선의 교점 작도 : 네 점 A, B, C, D가 주어졌다. 그럴 때 직선 AB와 직선 CD가 교차하는 점을 작도할 수 있다.
- 적당한 r를 잡아 원 를 작도한다.
- 직선 AB를 원 에 inversion한다. 중심을 지나므로 그대로 그 직선으로 남게 된다.
- 직선 CD를 원 에 inversion한다. 직선을 inversion 했으므로 원으로 바뀌고 점 A를 포함한다. 바뀐 원과 직선 AB의 교점 중 A가 아닌 다른 점을 P라 하자.
- 점 P를 에 inversion 한 점이,교점은 교점으로 대응하기 때문에, 우리가 찾던 점이다.
컴퍼스를 한 번만 쓰고 자를 쓸 경우
프랑스의 퐁셀레(Poncelet)[6]가 1822년, 독립적으로, 1833년 스위스의 쉬타이너(Steiner)[7]는 의해 밝혀졌다.
- Poncelet-Steiner정리 : '중심이 알려진 원이 하나가 고정되어 있는 평면'에서 자만 쓰는 작도는 컴퍼스를 자유롭게 쓰는 작도와 등가다.
주어진 원에 대해 그 중심을 작도할 수 있으지만(Euclid 원론 3권, 정리1) 자만으로는 작도할수 없다는 것을 쉬타이너는 보였다.[8] 원이 하나 주어진 것으로는 부족하고 '그 중심이 알려진' 이라는 조건이 중요하다. 따라서 우리에게 중심이 알려진 원이 하나 그려진 어떤 종이가 있거나, 컴퍼스를 한번만 쓸 수 있다면 '자와 컴퍼스'가 하는 모든 작도 문제를 할 수 있다.
증명을 위해서는, 자는 '직선과 직선의 교점'만을 새로 더할 수 있기 때문에,
- 어떤 원과 직선의 교점을 찾아 더하고
- 원과 원의 교점을 찾아 더할 수 있다는 사실을 보여야 한다.
아래를 풀기 전에 먼저 '두 원의 radical axis'의 개념을 알아둘 필요가 있다.
- 정의 ( 어떤 원에 대한 점의 power ) : 어떤 원 에 대해 점 A의 power ()는 다음과 같이 정해진다.
따라서 원의 반지름보다 작은 쪽에서는 음수가 되고 원의 '바깥쪽'에서는 양수가 되며 원에서 멀어질수록 값은 커진다.
- 정의 ( 두 원의 radical axis ) : 두 원 에 같은 power를 갖는 점들의 집합 [9]
다음 문제를 차례차례 풀어보자. 마지막 두 작도가 우리가 보고자했던 사실을 확인시켜준다. 중심이 알려진 원이 하나 주어졌고, 자만 사용해서 작도해야 한다. 또는 컴퍼스를 한번만 써야 한다.
- 어떤 직사각형을 작도할 수 있다.
- 평행한 어떤 두 직선 이 주어졌고 직선 에 두 점 A, B 가 있다고 하자. 그럴 때, 선분 AB 의 중점을 작도할 수 있다.
- 정사각형을 작도할 수 있다.
- 어떤 직선 과 그 직선에 없는 점 E 가 주어졌다. 그럴 때, 점 E 을 지나고 에 평행한 직선을 작도할 수 있다.
- 어떤 직선 과 그 직선에 없는 점 E 가 주어졌다. 그럴 때, 점 E 을 지나고 에 수직인 직선을 작도할 수 있다.
- 어떤 길이 r 과 어떤 직선 과 그 직선의 한 점 C 가 주어졌다. 그럴 때, 직선 에 있는 점 중 C 에서 길이가 r 인 점을 찾을 수 있다.
- 두 점 와 길이 가 주어졌다고 하자. 그럴 때, 원 과 원 의 근축(radical axis)을 작도할 수 있다 :
- 어떤 직선 과 점 M 과 길이 r 가 주어졌다고 하자. 그럴 때 점 M 을 중심으로 하고, 길이 r 을 반지름으로 하는 원과 주어진 직선의 교점을 작도할 수 있다.
- 두 점 와 길이 가 주어졌다고 하자. 그럴 때, 원 과 원 의 교점을 작도할 수 있다 :
변형된 자를 쓸 경우
'순수한' 자만을 쓸 경우 표준적인 작도보다 근본적으로 축소된다. 그러나
- 거리가 r 만큼 떨어진 두 변을 한꺼번에 그릴 수 있는 평행자나,
- 직각이거나 직각보다 작은 어떤 각을 한꺼번에 잴 수 있는 자나,
- 각의 이등분기와 순수한 자가
있다면 위의 어떤 도구를 쓴 경우도 자와 컴퍼스의 작도와 본질적으로 같다는 것이 19세기 말 오스트리아의 아들러가 증명하였다.[10]
보다 복잡한 도구를 쓸 경우
보다 복잡한 도구들이라는 말의 정의가 아직 불분명하다. 고전적 작도 문제들을 풀면서 복잡한 도구들의 구체적이 예들이 나온다. 막연한 채로 여기서는 '보다 복잡한'이라는 말은, 자와 컴퍼스보다 더 많은 기능을 할 수 있어서 근본적으로 확장하는 것을 말하는 것으로 이해하자. 그리고 지금까지 개발된 '기하학적 도구'들을 살펴보고 새로운 도구를 생각해보자.
예를 들어
- 컴퍼스와 두 점을 표시할 수 있는 자만 있어도 각의 삼등분 문제를 풀 수 있다는 것을 아르키메데스가 보였다 : 각의 삼등분 문제 참고.
나중에 보완
- 무한 단계를 가정한다면 ( ) : 무한히 근사적으로 가까운 값을 얻을 수 있다. 여기에 만약 '수렴'의 개념을 받아들인다면 는 근본적으로 확장된다. , 타원 작도 가능할까? 이에 대해서는 따로...
Note
- ↑ 앞으로 만약 표준적으로 작도 가능한 모든 문제들의 집합을 라고 한다면, 문제의 조건 를 살짝 바꾼 조건 로 했을 때, 는 어떻게 변화할까? 바뀐 조건에서 풀 수 있는 모든 문제들의 집합을 라고 쓰기로 하자. 그 때, 앞으로,
- '근본적으로 가 축소된다'라는 말은
- '근본적으로 가 확장된다'라는 말은
- 표준을 바꾸면 어떤 영향을 받을까 ?
- 정의하는데 쓰인 조건을 느슨하게 하면 작도 가능한 문제가 근본적으로 늘어날까? 또는 조건을 더 조이면 작도 가능한 문제도 근본적으로 줄어들까 ?
- ↑ Jørgen Mohr(1640 - 1697)가 쓰고 1672년에 나온 책 <Euclides Danicus> 에 들어있다고 한다. 당시 로마어로 쓰던 학계의 관행과 다르게 모어는 덴마크어와 그 자신이 오랫동안 살았던 네델란드 어로 썼다. (라틴어판도 함께 출판할 예정이었으나, 잘 안 되었던 듯 싶다. 아마 이것이 이 책이 250년 동안 잊혀졌던 이유와 연관되었을 수 있다.) 1928년에야 코펜하겐의 헌책방에서 젊은 학생이 이 책을 발견하고 그 해에 복사판이 출간되어 그때까지 마르케로니 정리로 알려졌던 것이 모어-마스케로니 정리로 인정받는다. 그는 유겐스에서서 배웠고, 라이프니츠와 살짝 교류했으며, 찌른하우스와 함께 머물렀고 일했다. 이 책의 첫부분은 유클리드 Elements 의 처음 6장을 정리했고, 뒷부분에서 컴퍼스만 쓴 작도 기하학을 보였다. 특히 이 안에는 컴퍼스만 써서 선분을 황금분할한 것이 들어있는데 이것은 역사적으로나 교육적으로 의미있다. Mohr proves in the book that a line segment can be divided in golden section with compass alone, and the historical and pedagogical importance of this theorem is discussed by Zühlke. MacTutor 에서 인용.
- ↑ Lorenzo Mascheroni (1750 이탈리아 – 1800 프랑스 파리). 자와 컴퍼스 문제와 Euler constant 의 자리수를 오일러가 계산한 16자리를 , 비록 계산이 틀린 부분이 있었지만, 32자리까지 늘였다.
- 오일러 상수 : 조화수열과 자연로그의 차의 수렴 :
- ↑ 직선은 그려져 Hard disc에 저장될 수 없다. 다만 메모리에 잠시 머물렀다 사라질 뿐이다. 다만 그 직선을 결정하는 두 점의 좌표는 저장하는데 별 문제 없다...
- ↑ 기하학적 변환의 작도 에서 inversion 점을 컴퍼스만 써서 작도 가능하다는 것을 보였다.
- ↑ 1788-1867. 도형기하학(descriptive geometry)의 창시자 몽쥐(Monge ;1746-1818)의 제자로 École Polytechnique에서 공부했다. 1812년 나폴레옹이 러시아를 침략할 때 장교로 참여했으나 전투의 패배로 1814년 본국으로 되돌아 갈 때까지 러시아의 사라또프에서 유형생활을 한다. 이 동안 원추 절단(conic section)과 사영기하(projective geometry)를 연구하고 'duality' 정리를 발견한다. 프랑스로 돌아가 군사공학과 수학 연구.
- ↑ 스위스에서 태어나 8세때, 유명한 교육자 페스딸로찌의 제자였다고 한다. 그 후 하이델베르크에서 공부하고 대수학자 야코비(Jacobi;1804 - 1851)의 추천을 받는다. 대수적 방법을 쓰는 해석, 또는 분석 기하(analytic geometry) 보다 고대 그리스의 전통적 기하학의 방법인 '종합 기하'(synthetic geometry)를 발전시켰다. 따라서 쉬타이너를 '아폴로니우스 이후 최고의 순수 기하학자'로 추앙하기도 한다.
- ↑ 자만으로 원의 중심작도 불가능를 참고. 따라서 원과 관련하여 원의 중심을 이용해야하는 작도를 자만 써서는 불가능하다. 그래서 자만을 쓰면 표준적인 작도 가능보다 근본적으로 축소된다.
- ↑
radical axis에 정리
- 두 원 의 radical axis는 직선 와 수직인 직선이다.
- 세 원이 주어졌을 때, 그 중 어떤 두 원도 동심원이 아닌 경우, 이 세 원의 radical axis는 겹치거나 평행하다.
- ↑ August Adler(1863 - 1923) : Mactutor자료
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia



































![{\displaystyle {\sqrt[{3}]{2}},2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63c9a0c116e0f5770d25d9d19a87907273f5f213)
![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)





















