Max Min Geometrical: 두 판 사이의 차이
(차이 없음)
|
2007년 11월 7일 (수) 21:36 기준 최신판
고대부터 현대까지, 실용적인 목적에서부터 과학적 발견에 이르기까지, 세계의 구성에 대한 철학적 인식[1]과 증명의 논리성에 이르기까지, max-min 문제는 수학의 세계에서 엄청난 중력을 가진 별과 같다. 이 문제를 풀기 위해 수학의 도구들을 끌어들였고 새로운 길을 트는 계기가 되기도 하였다. 우리는 여기서 역사적인 흐름을 따라가면서 max-min 문제들 중 역사적으로나 논리적으로 중요한 의미를 갖는 유명한 문제들을 만나게 될 것이다.
Min-Max 문제는 일반적으로 다음과 같은 형태를 가진다 :
- 어떤 조건이 주어졌다고 하자. 그럴 때, 원하는 최대 또는 최소가 되도록 하는 집합[2]을 찾아라.
여기서는 이와 같은 문제를 max-min 문제로 부르기로 하자. max-min 문제는 언뜻 단순해보이지만, 조건이 무엇이냐에 따라 우리가 원하는 값이 어떤 형태인가에 따라 문제와 풀이의 스펙트럼이 매우 넓다. 그리고 과학자들이 주어진 상황을 해결하는 데 있어, 그리고 산업에서도 이 문제는 폭넓게 응용된다. 여기서는 고대 그리스 시대부터 알려진 중요한 두 문제인 헤론 문제와 '같은 둘레' 문제에 대해서 살피고 그 문제들이 변형되면서 어떻게 일반화되거나 새로운 수학의 영역을 개척해가는지 수박 겉핥기로 살피도록 하자. 앞으로 우리가 따로 볼 문제들에 대한 소개도 아울러 한다.
헤론의 문제
헤론(Heron; AD 10 - 75 로 추정)은 고대 그리스 시대의 중요한 기하학자이자 과학기술자였다. 그가 밝혀낸 것 중 삼각형의 세 변과 면적의 관계를 밝힌 정리는 우리에게도 낯설지 않다. [3] 아래의 최소 길이의 문제도 마찬가지로 학교 교육에서 꽤 알려지고 많이 응용되는 문제다.
 원조 헤론 문제
원조 헤론 문제
- (헤론 문제[4]) 평면에 직선이 주어졌고 그 직선의 한 쪽 평면에 두 점 A, B 이 주어졌다. 그때 두 선분 사이의 거리의 합 이 최소가 되도록 하는, 직선 위의 점 M 을 찾아라.
두 점 중 한 점을 직선 에 대칭(symmetry)한 점과 나머지 한 점을 이어 직선 과 교차한 점이 바로 우리가 찾는 점이다. ( 왜 그럴까? 스스로 밝혀보라. 증명은 헤론 문제들에 대한 증명 을 참조하라.
문제와 해답이 모두 단순하고, 통쾌함을 느낄만큼 분명하다. 해결에서 쓰인 유일한 개념은 대칭(symmetry) 이다. 주어진 점과 직선에 대해 대칭을 이용하여 미리 한 점을 가정하고 그 점이 다른 어떤 점보다 최소 길이를 갖을 수 밖에 없다는 것이 풀이의 핵심 논리다. 그리고 그 점은 자와 컴퍼스를 써서 찾아낼 수 있다. 그런데 이 단순한 성질은 그저 아름답기만 한 것이 아니라 현실 세계에서 매우 중요하게 쓰인다. 이에 대해서는 다른 곳에서 더 다루기로 한다.
위의 문제의 조건을 바꾸어 보면서 풀이를 찾아보자. 이는 문제의 본질에 대한 깊이 이해하고 수학적 사고를 하는데 도움을 많이 줄 것이다.
 헤론 문제의 변형 : '직선 하나'의 가정을 바꾼 경우
헤론 문제의 변형 : '직선 하나'의 가정을 바꾼 경우
아래와 같이 조건 부분을 바꾼 문제를 생각해보자.
- (직선이 둘 주어졌을 때의 헤론 문제) 만약 두 개의 직선 이 주어졌다고 하고 두 직선이 이루는 각에 두 점 A, B 이 주어졌다고 하자. 그럴 때, 거리의 합 이 최소가 되도록, 직선 에 있는 점 P, 직선 에 있는 점 Q를 찾아라.
바꾼 문제 1의 경우 조건을 줄 때, 하나의 직선이라는 가정을 더 일반적인 가정으로 한 경우다. 먼저 바꾼 1의 경우, 바뀐 문제는 본질적으로 다른 문제가 아니다. 그런데 문제를 이렇게 바꾸어보면 어떨까? 마찬가지로 대칭개념에 기대어 해를 찾을 수 있다. 그런데, 직선이 두 개 주어졌기 때문에 풀이는 더 복잡해진다. 헤론 문제들에 대한 증명 에서 이에 대한 설명을 이어서 하겠지만, 그 전에 스스로 이 문제를 풀어보길 바란다. 문제에서는 점 P, Q의 위치를 미리 정했지만, 문제를 다음과 같이 바꾼다고 해보자. 조건 부분은 같고
- 그럴 때, 거리의 합 이 최소가 되도록, 직선 에서 한 점 Q, 직선 에 있는 점 P를 찾아라.
그렇다면 바꾼 문제에서 찾은 '꺽은 선'과 이 문제에서 찾은 '꺽은 선'은 같을까? 어떤 경우에 같고 어떤 경우에 달라질까? 문제를 더 일반화해 보자. 다시, 문제의 조건 부분은 같고
- 거리의 합 이 최소가 되도록, 직선 에 있는 점 하나, 직선 에 있는 점 하나씩인 점 P, Q를 찾아라.
이 문제는 두 개의 직선이 아니라, n 의 직선으로 더 일반화할 수 있다. (n은 1보다 같거나 큰 정수)
- Q : 주어진 직선이 n개인 경우의 문제를 만들고 스스로 풀이를 찾아보라.
 헤론 문제의 변형 : '두 점'의 가정을 바꾼 경우
헤론 문제의 변형 : '두 점'의 가정을 바꾼 경우
앞의 변형에 비해 언뜻 보면 아래 문제는 단순해보인다.
- (세 점이 주어진 Heron 문제) 평면에 직선 이 주어졌고 그 직선의 한 쪽 평면에 세 점 A, B, C 이 주어졌다. 그때 두 선분 사이의 거리의 합 이 최소가 되도록 하는, 직선 위의 점 M 을 찾아라.
이 문제는, 그러나, 보기 처럼 단순하지 않다. (스스로 풀어보라.) 위의 두 점일 때의 경우와 풀이 방법이 많이 달라진다. 문제는 비슷해보이지만 '대칭' 개념을 써서 풀어지지 않는다. 뿐만아니라 더 일반적으로 말해서, 기하학적인 작도의 방법으로 풀 수 없다. 대수적, 해석학적인 도구를 빌어 쓰는 'Variational 방법'으로는 풀 수 있다. Variational 방법 을 공부하면서 더 자세히 살펴보도록 하자.
 헤론 문제의 변형 : '직선'의 가정을 버리자
헤론 문제의 변형 : '직선'의 가정을 버리자
헤론 문제를 위의 문제를 해결할 때, 대칭 개념은 '직선'의 개념에 기대고 있기 때문에 만약 이 문제에서 '직선'의 가정을 바꾸어보면 해결 방식도 달라질 것이라고 미루어 짐작할 수 있다. 예를들어
- (일반화된 헤론 문제) 평면을 둘로 나누는 어떤 선이 주어졌고 나뉜 평면의 한 쪽에 두 점 A,B이 있다고 하자. 그럴 때, 두 선분 사이의 거리의 합 이 최소가 되도록 하는, 그 선에 있는 어떤 점 M을 찾아라.
라고 하고 문제를 바꾸었다고 하자. 이 문제는 물론 헤론 문제를 포함하는 일반화된 문제다. 주어진 선이 직선일 경우 대칭 개념을 써서 앞에서 한 것처럼 풀면 된다. 그런데 직선이 아니라면? 물론 풀이 방식은 달라질 것이다. 어떤 점을 미리 가정하고 그 점이 다른 점보다 최적의 점이라고 보이는 방식으로 증명 구상을 했다고 하자. 그런데 '평면을 둘로 나누는 어떤 선은 너무 광범위한 개념이라 어떤 '특별한' 점을 찾는 것은 불가능하다. 흔히 있는 일로 문제가 단순화될수록 일반적인 증명은 어려워진다. 우리는 기하학에서 매우 중요한 도형들 Conic Section의 경우에 대해 이 문제와 비슷한 경우들을 살펴보고 그 성질을 찾아볼 것이다. 이에 대해서는 Conic_Section_MaxMin에 대해 다루겠지만 우선 문제 하나를 스스로 풀어보도록 하자.
- Q : 타원의 내부에 두 점 A, B 이 있다. 타원에 있는 어떤 점 M 을 잡아야 두 선분의 거리의 합 이 최소가 되도록 할 수 있을까?
 풀이가 비슷한 문제 : 새로운 문제로
풀이가 비슷한 문제 : 새로운 문제로
앞의 경우는 문제는 비슷한데 풀이가 달라진 경우라면, 아래 문제는 겉모양은 달라보이지만 풀이 방식이 비슷한 경우다.
- 평면에 볼록 사각형이 있다. 사각형의 꼭지점들과 이어서 그 선분의 길이의 합이 최소가 되는 점 M 을 찾아라.
이 문제는 헤론의 문제를 푼 것과 유사하다. 대신 여기서는 대칭 개념도 필요없다. (스스로 풀어보라) 헤론 문제의 해법이나 이 문제의 해법이나 비슷한 점은 바로 이렇다. :
- 어떤 특정한 점을 찾는다.
- 다른 모든 점은 그 점으로부터 이루는 길이의 합보다 길다.
다시 말해, '다른 모든 점들보다 우리가 선택한 점보다 못하다' 를 보이는 방법이다. [5] 그런데 방금 던졌던 이 문제를 다음과 같이 '쉽게' 고쳤다고 해보자.
- 평면에 삼각형이 있다. 삼각형의 꼭지점들과 이어서 그 선분의 길이의 합이 최소가 되는 점 M 을 찾아라.
이 문제를 찾는 것은 언뜻 생각했던 것처럼 그리 단순하지 않다. 이 문제는 역사가 길고 기하학적으로 깊은 뜻이 담긴 문제다. 이 문제는 토리첼리-스타이너 문제와 쉬타이너 망 에서 따로 살펴 보기로 한다.
같은 둘레 문제
이 문제는 수천년의 역사를 가진다. 고대 로마의 시인 베르길리가 지은 영웅서사시 에네이다[6]에도 이와 관련한 일화가 있다. 일화는 나중에 올리기로 하고... 간단히 쓰면 아래와 같다. 정해진 길이의 밧줄을 주고 그것으로 땅에 둘레를 만들 수 있는 만큼 땅을 주겠다고 한다. 이 디도나는 먼저 밧줄을 풀어 실로 만든다. 그리고 바닷가로 나가 해안선쪽으로는 실을 치지 않고 땅쪽으로만 둘레를 친다. 바닷가가 직선이라고 가정할 때,
- 길이가 1 km인 실로 최대한의 면적의 땅을 갖도록 도형을 만들어라.
문학적 작품에서 인용하다보니 앞의 예에서는 '길이가 제한된 실' 이라든가 '바다에 붙은 직선의 해안선' 과 같은 문구가 있었다. 일반적으로 같은 둘레를 가진 최대 면적을 찾는 문제는 다음과 같은 유형이다. 그려보기 쉬운 3차원 유클리드 공간에서 예를 들자. 풀 수 있는 한 스스로 풀어보라.
- 어떤 길이가 주어졌을 때, 그것을 둘레로 하는 삼각형 중 최대 면적을 갖는 삼각형은 어떤 삼각형인가?
- 어떤 길이가 주어졌을 때, 그것을 둘레로 하는 볼록 n각형 중 최대 면적을 갖는 것은 ?
- 어떤 길이가 주어졌을 때, 그것을 둘레를 하는 폐곡선 중 면적이 최대가 되는 도형은?
- 어떤 면적이 주어졌을 때, 그것을 표면적으로 하는 도형 중 부피가 최대가 되는 도형은 ?
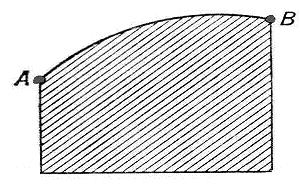
이처럼 정해진 어떤 '양(量)'이 있을 때, 최대나 최소와 같은 특별한 값을 갖게 하는 어떤 도형을 찾는 문제를 이른바 '같은 둘레 문제'라고 단순화 시켜 말해본 것이다. 이런 류의 문제는 17세기말 야곱 베르눌리, 18세기 중반 오일러가 다음의 형태로 질문을 바꾸면서 보다 일반적인 해법을 찾아가는 방향으로 틀을 잡아간다.
- (베르눌리) 길이가 주어진 모든 곡선 중에서 그 곡선의 길이에 따라 변하는 어떤 양(量, 또는 값)이 최대나 최소가 되는 곡선을 찾아라.
- (오일러) 주어진 두 점 A, B를 지나면서 길이가 주어진 어떤 곡선들이 있다고 하자. 그 때 이루는 '휜 사다리꼴'의 면적이 최대가 되는 곡선은 어떤 곡선인가?
이런 방향전환은 대수적 기술의 발달과 해석학적 개념이 발달하면서 수학을 그 언어들로 일반화하는 경향을 나타낸다. 이런 경향은 어쩌면 필연적인 흐름이었다고 해도, 보다 보다 논리적인 직관과 작도 가능과 같은 constructive한 개념을 담고 있는 기하학적인 해법을 만나는 것은 여전히 매력적이고 지적 아름다움과 만나는 일이다.
위에서 두번째 문제는 첫번째 문제의 일반형이다. 이 문제에 대해서는 이미 아르키메데스나 제노도로스 [7]가 시도했고 그 답으로 정 n각형이라는 것을 밝혔다. 그리고 세번째 문제에 대한 답이 원이라는 사실도 이미 알고 있었던 것으로 추정한다. 그러나 이는 오랜 세월 증명이 되지 않았다.
베르글리의 서사시에서 페니키안의 공주 디도나는 해안선을 따라 최대 면적을 얻기 위해 반원 모양을 만들어 새로 정착할 땅을 얻게 된다. 디도나 공주는 최적의 답을 찾은 것일까? 같은 둘레 문제의 답은 원이고 이런 결과는 이미 당시에도 알려진 것으로 추정된다. 만약 그렇다면 바닷가로 해서 반원일 경우 최대 면적의 땅을 갖게된다. 그렇다면 과연 원이 같은 둘레 문제의 최적의 답이라고 자신할 수 있을까? 이를 위한 최선은 수학적으로 증명하는 일이 남는다. 그러나 이 증명은 그리 쉽지 않았다. 엄격하게 흠이 없는 증명은 19세기 말에서야 가능했다. 19세기 중반 기하학의 대가 쉬타이너(J.Steiner ; 1796 – 1863) 가 다음과 같이 증명했다.
- 어떤 길이가 주어졌을 때, 그 길이로 도형을 만들어 최대 면적이 나오려면 다음과 같은 세 성질을 만족해야 한다.
- 도형은 볼록이다.
- 도형의 지름은 둘레 뿐만 아니라 면적도 반으로 나눈다.
- 도형의 어떤 점에서도 지름을 이루는 점들과 이루는 각은 직각이다.
- 따라서 도형은 원이다.
'기하학적인' 해법이다. 놀랍도록 명쾌하다. 증명에 쓰인 도구 또한 복잡하지 않다. 사람들을 놀라게 할만하고 어디에도 흠이 없는 것처럼 보인다. 실제로 당시에는 이를 완벽한 증명으로 받아들였다. 그러나 논리적으로 치명적인 약점이 도사리고 있었다. 이를 해결하여 완벽한 증명으로 받아들인 것은 19세기 말의 일이다. [8] 우리는 이 문제에 대해 보다 Isoperimeter_Steiner에서 더 자세히 살펴보기로 한다.
판야노-슈바르츠 문제
판야노 [9]는 다음과 같이 흥미로운 질문을 던진다.
- 판야노 문제 : 예각 삼각형 ABC가 주어졌다고 하자. 그럴 때 각 변에 한 꼭지점을 두고 둘레가 최소가 되는 삼각형이 있다면 어떤 삼각형일까?
이 문제가 갖는 '기초적'(elementary)인 성격 덕분에 이 문제에 대한 증명도 여럿이다. 게 중에는 보다 명쾌해서 매력적인 것이 있고 어떤 것은 그보다 그렇지 않다. 그리고 이 문제는 삼각형의 내부에 '이상적인 거울'을 만들어 변의 어디에선가 빛을 쏘았을 때 반사하는 운동의 성질을 보는 것과 같은 흥미로운 물리적 성질들과 이어진다.
문제에서 준 조건 '예각 삼각형'이 아무래도 마음에 걸린다. 따라서 문제를 일반화 하여 다음과 같이 바꾸어볼 수도 있다.
- 일반화된 판야노 문제 : 삼각형 ABC가 주어졌다고 하자. 그럴 때 각 변에 한 꼭지점을 두고 둘레가 최소가 되는 삼각형이 있다면 어떤 삼각형일까?
이와 관련한 문제를 Fagnano_Schwartz_Problem 에서 살펴 볼 것이다.
Note
- ↑ L. Euler(1707-1783) "어떻게든, 최대와 최소의 개념이 보이지 않는 것은 세상에 발생하지 않는다."
Carl.L. Siegel(1896 - 1981;수론의 대가) "라이프니쯔에 따르면, 세계는 가능한 모든 세계에서 가장 좋게 드러나고, 따라서, 세계의 법칙은 극값의 원칙들로 나타낼 수 있다." - ↑ 여기서 집합은 점, 선분, 도형과 같은 것을 원소로 가질 수고 그보다 더 일반적인 경우도 가능하다. 이에 대한 구체적인 예들이 앞으로 더 나올 것이다.
- ↑ 세 변의 길이와 면적의 관계를 나타낸 유명한 정리는 다음과 같다.
- 어떤 삼각형의 세 변의 길이가 a, b, c 라고 하고, 이 변들의 길이의 합을 반으로 나눈 수를 s라고 하자. (. 그럴 때, 면적 S 는
- ↑ 헤론이 쓴 저작 중 Catoprica 에는 주로 거울과 반사에 대해 다루고 있는데, 여기서 아래의 문제, 다시 말해 직선을 거울로 생각하고 빛이 쏘아서 반사하는, 최소의 길이, 그때 이루는 각의 성질을 다루었다고 전한다.
- ↑ 작도 가능의 문제를 풀 때도 주로 이런 방식을 썼다. 필요한 집합을 찾았다고 가정하고 그것이 작도할 수 있음을 보인다음, 그 점이 제대로 찾은 점일 수 밖에 없다는 것을 증명하는 방식이었다. 그렇다면 이 점을 과연 어떻게 찾을 수 있을까 ? 직관에 의해? 비슷하게 작도해보면서? ...
- ↑ Publius Vergilius Maro. 보통 Vergilius라고 부른다. 영어식으로 Virgi 또는 Vergil. 서사시의 이름도 영어식으로는 Aeneis. (영문) 위키페디아 참조
다음은 책소개 : 베르길리우스, 『아에네이스』 Vergilius, Aeneis. 로마의 공화정이 쇠하고 제정이 시작되던 때, 기독교가 이제까지의 이교적인 문화를 물들이기 시작하던 때, 새로운 번영과 회의주의적 정신이 기존의 가치체계를 위협하던 때인 기원전 1세기에 태어난 이 대표적 서사시는 영웅적 과거에 비추어 현재 벌어지는 사건의 의미를 풀어내고 국가의 운명을 가늠해 보려는 건국신화이기도 하다. 이 작품은 영웅적인 인간과 신의 관계를 살피고 있다는 점에서 뿐만아니라, 성경을 제외한다면 서양에서 가장 널리 알려졌고 가장 커다란 영향력을 지속적으로 행사해왔다는 점에서 세속적 성서라 할만하다.(이종숙) - 서울대 추천도서에서 인용 - ↑ Zenodorus(200 BC - 140 BC) 참조. Zenodorus라는 개미의 종류도 있다... :)
- ↑ 19세기 중반부터 수학전반에 수학의 '논리적 기초'에 대한 반성과 연구가 폭발적으로 왕성하였다는 점을 상기하자.
- ↑ Fagnano dei Toschi ;1682-1766 : 이탈리아 기술자, 수학자. 미분, 고차 방정식 풀이, elliptic function 분야 연구.
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia







