Fermat Toricelli Steiner Point
여기서 볼 문제에 대해 기록으로 전하는 것은 아마도 이탈리아의 수학자이자 과학자였던 비비아니(Vincenzo Vivian; 1622-1703) [1]의 저작 일명 '최대최소문제에 대하여'[2] 일 것이다. 이 책에는 다음과 같은 문제가 있다고 한다.
- (토리첼리-쉬타이너 문제) 한 직선에 있지 않은 세 점 A, B, C 가 있다고 하자. 어떤 점 X 에서 이 세점으로의 길이의 합 |AX + BX + CX | 이 최소가 되는 X를 찾아라.
이 문제는 우리가 앞의 MaxMin 서론 에서 보았듯이 MaxMIn 문제의 전형적인 형태이며 Heron 문제를 증명하는 방식과 유사한 방식을 썼던 네 점 문제와 닮았다. 네 점 문제를 다시 써보자.
- 평면에 볼록 사각형이 있다. 사각형의 꼭지점들과 이어서 그 선분의 길이의 합이 최소가 되는 점 M 을 찾아라.
위의 문제는 문제의 조건에서 '네 점'을 가정함으로써 특이점을 가정하기 쉬었고 (위의 문제는 대각선의 교점이라는 특이점을 가정했다.) 그 특이점과 다른 모든 점들을 그 점과 비교해서 문제의 결론 부분을 만족하지 않는다는 것을 보이는 방식을 택했다. 다른 모든 점들이 우리가 가정한 특이점 보다 길이의 합이 클 수 밖에 없기 때문에 우리의 선택이 옳았다는 방식이다. 그런데 토리첼리-쉬타이너 문제처럼 삼각형이 주어진다면 문제는 그리 간단하지 않아보인다.
이 문제 해답이 되는 '특이점'을 발견한 사람은 갈릴레이의 제자 토리첼리[3](Evangelista Torricelli;1608-1647) 인 것으로 전한다. 세 점의 어떤 각도 120도 보다 작을 때, 이 점이 세 꼭지점과 거리의 합이 최소가 된다. 이 점이 이루는 세 각은 모두 120도 라는 것은 까발리에리[4]가 밝혔다.[5]이 문제는 페르마도 푼 것으로 알려졌지만, 아름다운 기하학적인 증명을 만나기까지 다시 몇 백년이 흐른다. 19세기 중반 대기하학자 야곱 쉬타이너가 그 주인공이다.
우리는 여기서 이 문제에 대한 여러 증명을 살펴보고 이 점을 관찰하며 수학적 상상의 날개짓을 해보자.
토리첼리 점의 작도
세 점 A,B,C 가 주어졌다고 할 때, 세변 AB를 한 변으로하는 정삼각형을 작도하고, 마찬가지로 BC, AC에 대해서도 이와 같이 한다. 이 세 정삼각형을 둘러싼 원을 작도해보자.
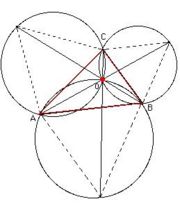
- (토리첼리 점)삼각형 안에서 세 원이 한 점에서 교차할 때, 이 점을 '토리첼리 점'이라고 한다.
앞에서 이야기했듯 토리첼리 점은 삼각형의 4대 특이점 [6]과 더불어 삼각형의 특이한 점으로 특별한 성질을 갖는다. 토리첼리가 발견한 이 점 T는 특별한 성질을 갖는다. MaxMin과 관련하여 다음과 같은 성질이 있다.
- 그 점 T에서 세 각은 세 변을 120도로 바라본다. (다시말해, T 와 꼭지점들을 이어 만들어진 세 각은 모두 120도 이다.)
- 꼭지점에 이른 거리의 합이 최소가 되게 하는 점이다.
앞의 120도 성질은, 토리첼리 정의와 등가다. 다시 말해 토리첼리 점에서 세 변으로 항상 120도이고 어떤 삼각형에서 각 변으로 120도로 바라보는 점은 토리첼리 점이다. ( 스스로 밝혀보라.) 따라서
- (토리첼리 점)삼각형 안에서 한 점에서 각 변으로 120도로 바라본다면 이 점을 '토리첼리 점'이라고 한다.
그런데 삼각형의 4대 특이점과 다른 성질이 있다 : 삼각형의 4대 특이점은 모든 삼각형에 대해 항상 존재하는데, 토리첼리 점은 그렇지 않다.
위의 사실들을 종합하여 볼 때, 주어진 세 점에서 거리의 합이 최소가 되는 MaxMin 문제는 다음과 같은 정리로 집약된다.
- (정리) 한 직선에 놓이지 않은 세 점으로부터 거리의 합이 최소가 되는 점은, 만약 있다면, 토리첼리 점이다.
최소 거리가 되는 점이 위의 성질을 갖는다는 사실을 증명하는 방법은 한두가지가 아니다. 여기서는 그 중 몇 개를 살펴보고 증명에 담긴 뜻을 새겨보기로 하자.
토리첼리 점 에서 보듯, 토리첼리점이 존재할 조건은 주어진 삼각형의 세 각이 모두 120보다 작을 때 이므로 위의 정리는 다음과 같이 옮겨 쓸수 있다.
- (정리) 한 직선에 놓이지 않은 세 점이 이루는 삼각형이 예각 삼각형이면, 거리의 합이 최소가 되는 점은 토리첼리 점이다.
만약 예각 삼각형이 아니라면? 어떤 직선 위에 있지 않은, 주어진 세 점으로부터 거리의 합이 최소가 되는 점은 어디에 있을까?
- (정리) 한 직선에 놓이지 않은 세 점이 이루는 삼각형이 예각 삼각형이 아니면, 거리의 합이 최소가 되는 점은 각이 최대가 되는 꼭지점이다.
- (애벌 증명)
- 가장 큰 각을 A라 하고 어떤 점 M 이 각 A 사이에 있을 때와 아닐 때로 나누어본다.
- 어떤 경우든 선분의 길이의 합 MA + MB + MC > AB + AC다. (각 A 사이에 있을 때 아래 쉬타이너 증명의 방법을 쓸 수 있다.)
쉬타이너의 증명
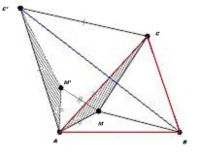
대기하학자 쉬타이너의 증명은 단순하고 명쾌하며 대단히 기하학적이다. 먼저 증명을 보자.
- 주어진 삼각형의 내부에 어떤 점 M 을 찍어 꼭지점과 모두 연결한다.
- 꼭지점 하나 (여기서는 A)를 정해 그 점을 기준으로 60도 회전한다. 오른쪽 그림과 같이 옮긴다. M M', C C'
- 그렇다면 M에서 세 꼭지점으로 길이의 합은 C'M'MB와 같다. (자세히 풀어보라)
따라서 C'B가 직선으로 있을 때, 길이의 합은 최소가 된다.
- 60도를 회전하여 180도가 되니, 각 BMA + 각 AMM' = 180, 따라서 찾으려고 했던 M에서는 각 BMA가 120도일 때 최소길이가 된다.
- 마찬가지로 각 AM'C' + 각 AM'M = 180, 따라서 AM'C' 는 120 이고 각 AMC도 120도.
- 따라서 M이 우리가 찾던 조건을 만족하면 세 변으로 모두 120도 씩을 이룸.
통쾌하다. 게다가 이 방식은 고대 그리스 시대 Heron 정리의 증명 처럼 순수기하학적인 증명이라는 법통을 잇고 있다.
다른 증명
이 증명은 WIM에 있는 방법이다. 증명의 큰 틀은 다음과 같다.
- 우리가 찾는 점 M 은 A, B, C 중 하나거나, 아닐 것이다. 따라서 두 경우로 나눈다.
- A, B, C 중 하나일 때는 각이 가장 큰 꼭지점이 찾는 점이다.
- A, B, C 중 하나가 아닐 때 다음의 사실을 주목해야 한다 : 중심을 C로 잡고 반지름을 CM로 하는 원을 작도하면 점 A, B는 원의 '바깥에' 있다. 최소거리라는 가정에 모순이 나온다. 이 사정은 점 A와 선분MA ; 점 B와 선분 MB 로 해도 마찬가지다.
- 그렇다면 M에서 A, B가 최소가 되는 점이 우리가 찾는 점이다. 이는 Conic Section 과 MaxMin 에서 보았듯이 헤론 정리의 확장이다. 따라서 점 M에서 접선과 AM과 MB가 이루는 각이 같을 때 최소가 된다.
- 이는 A를 중심으로 반지름이 MA인 경우나 점 B 를 중심으로 선분 MB 를 반지름으로 해도 마찬가지다.
- 따라서 M은 토리첼리 점이다.
- 우리는 지금까지 우리가 찾는 점이 꼭지점 중 하나이거나, 아니라면 각 변을 120도로 보는 토리첼리점이라는 것을 밝혔다. 그렇다면 어떤 경우에 꼭지점이 되고 어떤 경우에 토리첼리 점인지만 밝히면 된다.
- 가장 큰 각이 A라고 가정하고 변 AB, AC를 현으로 하는, 120도인 호들를 작도한다.
- 교차점은 A와 다른 한 점이 있을 것이다 (왜 그런가?)
- 다른 한점은 삼각형 ABC 안에 있거나 밖에 있을 것이다 : 예각삼각형이라면 안에 있고 그렇지 않으면 밖에 있다. (왜 그런가?)
- 밖에 있다면 우리가 찾는 점은 A다.
- 안에 있다면 선분 길이의 합 MA + MB + MC 이 AB + AC보다 작다는 것을 보임으로써 증명은 끝난다. (직접 해보라. WIM 그림.212)
이 증명은 쉬타이너 증명보다 길고 복잡하며 '덜 기하학적'이다. 대신 여기서는 주어진 삼각형이 예각삼각형이 아닐 때, 우리가 120도를 포함하는 호를 작도하였을 때 '꼭지점이 아닌 두번째 교차하는 점'에 대해 궁금증을 품게 만든다. 도대체 그 점은 어떤 성격을 가질까? 그저 우연히 있는 어떤 점일 뿐인가? 아니면 어떤 MaxMin의 뜻을 갖는 점일 수 있지 않을까?
- 주어진 삼각형이 예각삼각형이 아닐 때 가장 큰 각을 이루는 양쪽 변에 120도의 호를 작도했을 때, 삼각형의 '밖에'서 교차하는 점 M은, 두 '멀리 있는 꼭지점과의 길이의 합에서 가까이 있는 꼭지점의 길이의 차가 최소가 되는 점이다.
다시말해, 두 호의 교차점이 A와 M이라고 했을 때
- M은 MB + MC - MA 가 최소가 되는 점이다.
또 다른 증명
WIM, 8-5-4. 그림 214
문제의 일반화 : Steiner Network[7]으로
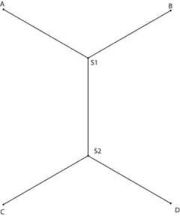
앞에서 우리는 세 점이 주어졌을 때의 문제를 보았다. 그리고 서론 부분 에서 언급했듯 네 점 문제도 살펴 보았다. 네 점의 최단 거리는 대각선의 교점이었다. 끝?!? Stop! 네 점 문제를 다시 보기로 하자.
- 사각형이 주어졌을 때 네 점을 이어 거리의 합이 최소가 되는 점을 찾아라.
라는 문제였다. 그러나 이 문제를 이렇게 바꾸면 어떻게 될까?
- 사각형이 주어졌을 때, 네 점을 이을 수 있는 거리의 합이 최소가 되는 점들을 찾아라.
다시말하면
- 사각형 모양으로 퍼져이는 네 도시를 가장 짧은 거리로 잇는 길을 설계하라.
라는 현실적 문제의 수학적 변형인 셈이다.
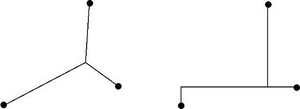
세 점이 주어졌을 때도 마찬가지다. 오른쪽 그림의 경우처럼 여러가지 방법이 있을 수 있다. 뿐만 아니라 위의 문제는 어떤 n 개의 점이 주어졌을 때 어떻게 될까? 그 일반적인 해법이 있을까 ? 하는 궁금증이 들 수 밖에 없다. 이는 단순히 우리가 페르마-토리첼리-쉬타이너 문제의 일반화라는 수학적인 문제로서만 아니다. 이는 현실적으로 아주 자주 부딪히게 되는 문제인 것이다.
- 여러 도시를 잇는 길을 만들 때
- 천연가스나 석유관을 여러 도시에 배분하며 나르는 공사를 할 때
의 최단거리 길찾기 문제들을 떠올려봐도 어렵지 않게 짐작할 수 있다. 이 뿐만 아니다...
우리는 쉬타이너 최단거리 문제 에서 이를 보도록 하자.
Note
- ↑ 기압계 발명가, 갈릴레이, 토리첼리의 제자. conic section과 maxmin 문제 연구자.
- ↑ 당시의 관행처럼, 라틴어로 된 책의 제목은 길다. 'conic section에 대한 아폴로니우스의 다섯번째 저작은 최대 최소값에 대한 최초의 연구이며 이 위대한 기하학자의 가장 뛰어난 업적이다' 라고 한다.
- ↑ 갈릴레이의 마지막 저작 '역학에 대한 대담'을 노년의 스승이 부르고 이를 받아 쓴 제자라고 알려졌다. 물리학자로서 높이 h인 통에 액체가 담겼을 때 새어나오는 속도 v 말한 아래의 토리첼리 법칙으로 유명하다. g는 중력가속도다.
- ↑ Bonaventura Francesco Cavalieri ; 1598–1647
- ↑ 이 밖에도, 토리첼리 점은 삼각형의 다른 특이점들, 예를들면, 내심, 외심, 무게중심과 같은 점들 처럼 여러가지 특별한 성질을 가진다. Torricelli_Point
- ↑ 내심, 외심, 무게중심, 수심을 말한다.
- 무게중심: 삼각형의 3개의 중선이 만나는 점이고, 이 점은 각 중선을 2:1로 내분한다.
- 수심: 삼각형의 3개의 꼭지점에서 대변에 내린 수선이 만나는 점.
- 내심: 삼각형의 3개의 내각의 이등분선이 만나는 점이고, 내심은 삼각형의 세 변을 접하여 지나는 원의 중심이 된다.
- 외심: 삼각형의 3변의 수직이등분선이 만나는 점. 삼각형의 세꼭지점을 지나도록 둘러싼 원의 중심이 된다.
- 방심: 삼각형의 한 내각의 이등분선과 다른 2개의 꼭지점에 대한 외각의 이등분선과 만나는 점. 한 변과 다른 2변의 연장선상에 접하는 원의 중심이 된다.
- ↑ Steiner Tree 라고 부르기도 한다.
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia

