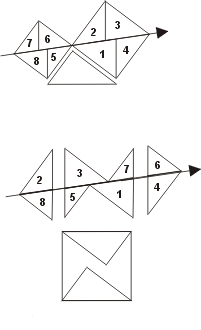
Pythagoras Th Proof1

피타고라스 정리 증명 : 조각내어 비교하기

눈으로 보면서 비교해 볼 수는 있는 방법부터 시작해보기로 하자. 피타고라스 정리를 증명하라는 문제에 맞닥뜨렸다면 어떻게 할까? 가장 우선 생각해볼 수 있는 것이 조각을 내어 비교해보는 방법이다. 누군가는 이렇게 말할 수 있는 것이다.

" 자, 작은 두 개의 정사각형을 쪼갠 조각이 큰 정사각형의 조각과 하나씩 대응하잖아? 그러니까, 직각을 이루는 두 변으로 만든 작은 두 정사각형의 넓이의 합은 빗변으로 정사각형을 이루는 큰 정사각형의 넓이와 같은 거지."

자연스러운 접근 방법이다. 이렇게 마음 먹고 접근하는 방식은, 물론, '어떤 도형의 넓이는 그것을 이루는 조각으로 쪼개어 더할 경우 같다.' 라고 하는 '더하기 공리'가 밑받침이 되고 있다. 이미 알려진 증명 방법은 많다. 하나하나 보면서 짚어가도록 하자.

쪼갠 조각을 비교하여 같다는 것을 보이는 증명들

에프쉬테인의 쪼개기

먼저 왼쪽 그림, 에프쉬테인이 한 증명을 보자. 쪼개기 위한 작도는 아래 순서로 한다.

작은 삼각형의 두 꼭지점 E, F 을 잇는다. 이 직선은 반드시 꼭지점 C 를 지난다. (왜 그런가?)
작은 삼각형들의 안쪽에 큰 사각형의 서있는 변들을 연장하여 만나는 점을 찾는다. 그 점에서 나머지 꼭지점으로 잇는다.
꼭지점 C 를 지나면서 방금 새로 그은 직선과 수직인 직선을 작도한다. 큰 사각형의 한 변과 만나는 점을 D 라 하자.
작은 사각형의 한변 FB를 연장하여 CD 와 만나는 점을 얻는다. 그 점에서 EF와 CB에 평행하도록 긋는다.
작은 사각형의 한변 AE를 연장하여 CD 와 만나는 점을 얻는다. 그 점에서 EF와 AC에 평행하도록 긋는다.

여기서, 질문

- GH 는 BC 와 평행할까?

- 옆의 그림의 위쪽의 조각들을 아래와 맞춰보라. 여러 이동 들로 보일 수 있다. 어떤 이동들일까?

닐슨의 쪼개기

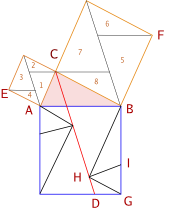
오른쪽 그림을 작도해보자. (닐슨 법)

작은 정사각형의 대각선을 잇는다.
꼭지점 C를 지나면서 변 AB 와 평행한 직선을 그어 작은 정사각형의 대각선을 이은 직선들과 만나게 한다.
남은 꼭지점 E 와 F 에서도 마찬가지로 AB 와 평행한 직선을 그어 작은 정사각형의 대각선을 이은 직선들과 만나게 한다.
꼭지점 C를 지나면서 작은 정사각형의 대각선들과 평행하도록 직선을 그어 만나는 점을 얻는다. 이 점은 에프쉬타인 법의 D 와 같다. (왜 그런가?)
작은 사각형의 한변 FB를 연장하여 CD 와 만나는 점을 얻는다. 그 점에서 CB에 평행한 직선과 CD와 직각을 이루게 한다.
작은 사각형의 한변 AE를 연장하여 CD 와 만나는 점을 얻는다. 그 점에서 AC에 평행한 직선과 CD와 직각을 이루게 한다.

닐슨이 한 방법은 에프쉬테인과 약간의 차이는 있지만, 쪼개진 조각들에 매겨진 번호들끼리 같다.

지금까지 세 방법의 공통점이 무언가? 세 방법 모두 쪼개진 조각들이 모두 삼각형으로만 이루어져 있다 ! 이제 그와 다르게 쪼개는 방법들도 이어서 보자.

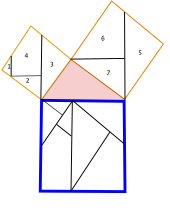
페리갈의 쪼개기

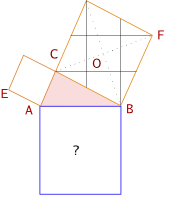
오른쪽 그림은 앞의 세 방법처럼 쪼개어 조각을 비교하는 방법과 같지만, 쪼개는 방식이 조금 다르다. 쪼개기 위해 작도하는 방법은 아래와 같다.

삼각형에서 직각을 이루는 변 중 큰 쪽의 정사각형의 중심 O 를 찾는다.
그 점 O에서 빗변과 수직인 직선을 긋고, 다음, 빗변과 직각인 직선을 긋는다.
빗변으로 이루는 정사각형을 쪼개기 위한 작도도 충분히 짐작할 수 있을 것이다. 변의 중점들을 잡아서 연결하고 ...

그렇다면 번호가 대응하는 조각들끼리 면적은 모두 같다. (직접 보여보라.) 이 방법은 어떤 점에서 특별할까? 모두 쪼갠 조각이 모두 사각형으로만 이루어졌다. 그리고 우리가 O를 잡은 정사각형의 네 조각은 모두 같다. 이것들보다 더 놀라운 것은 다른 데 있다. 이 방법으로 쪼개면,

대응하는 도형들의 대응하는 변들끼리 모두 평행하다 !

(직접 확인해보라.) 따라서 평행 이동만 써서 이들이 같다는 것을 보일 수 있다. 이는 우연이 아니다 ! 우리는 같은 조각으로 이루어짐에서

넓이가 같은 다각형들은 같은 조각으로 쪼개진다.

를 어렵지 않게 알 수 있다. '평행이동' 만으로 증명할 수 있다는 것이 우연이 아니라는 사실을 보이기 위해서는 위의 정리보다 더 강한 정리가 필요하다.

넓이가 같은 다각형들은 '평행한' 같은 조각으로 쪼개진다.

정말 그럴까? 이에 대해서는 상응하는 변이 평행하도록 쪼개기에서 더 자세히 다루기로 한다.

여기서 또 질문 : 점 O 가 중심이어야 한다는 조건을 조금 풀어주면 어떻게 될까? 왼쪽 그림처럼 AB 에 평행하거나 직각으로 이루어진 '작은 정사각형' 안의 어떤 점이든 O 로 잡으면 ?

알 나이리찌-회펠의 쪼개기

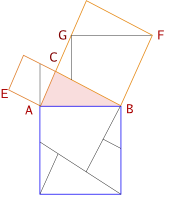
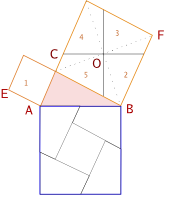
중세에 접어들면서 고대 그리스에서 꽃을 피운 수학은 아랍으로 중심이 넘어가면서 고대 그리스의 중요 저작들이 아랍어로 번역된다.^[1] 이 방법은 유클리드의 Elements 의 아랍어 번역본 주석을 실렸다고 한다. 10세기경 알 나이리찌의 방법이다. 회펠이 1824년에 약간 수정된 형태로 다시 증명하였다. 옆에서 볼 수 있듯 이 쪼개기는 깔끔하다. 작도를 보자. 쪼개는 방법은 충분히 짐작할 수 있을 것이다. 3번 삼각형을 빗변으로 이루어진 큰 삼각형에서 얻는 방법은 평행이동해서 꼭지점을 대응하도록 하거나, 그 삼각형의 빗변의 길이만큼 같게 작도하면 된다. 평행이동이나, 주어진 직선에 주어진 점으로부터 어떤 길이 만큼 작도하기는 자와 컴퍼스로도 충분히 작도가능하다. (작도가능의 기초 참조)

안쪽으로 정사각형 만들기

자, 그런데, 앞에서 해온 방법들을 다시 보자. 나름대로 장단점이 있고, 그것들로 부터 흥미로운 수학적 사실을 끄집어 낼 수 있다는 것은 더 있다가 보기로 하고 우선 짚고 넘어갈 것 부터 두드려보자.

직각삼각형에서 세 변마다 정사각형을 만들어 작은 두개의 정사각형을 쪼갠 조각들과 큰 정사각형을 쪼갠 조각이 같다.

는 것을 보이기 위해 '변에 정사각형을 쌓아올렸는데' 우리는 습관적으로 '바깥쪽으로' 쌓아 올렸다. 꼭 그래야하는 것은 물론 아니다. 따라서 앞의 증명들은 엄격하게 말하면 '바깥쪽으로 그려진' 모델에 대해 적용하는, 특수한 경우를 정해놓고 증명한 것일 뿐이다. 직각삼각형에 정사각형을 쌓은 또 어떤 경우들이 가능할까?

세 변 모두에서 바깥쪽으로 정사각형을 만드는 방법.
두 변은 바깥쪽으로 한 변은 안쪽으로 정사각형을 만드는 방법.
한 변은 바깥쪽으로 두 변은 안쪽으로 정사각형을 만드는 방법.
세 변 모두 안쪽으로 정사각형을 만드는 방법.

그렇다면 지금까지 우리가 한 증명들은 특수한 경우의 증명일 뿐이므로 받아들일 수 없는 것일까? 이 모든 경우에 대해 다 해봐야 하는 것일까?

여기서 잠깐 멈춰 알 나이리찌-회펠의 증명에서 한쪽이 접히는 경우를 보고 가자. 직각을 이루는 변 중 큰 변이 안쪽으로 접혔다고 가정하자. 앞에서 우리가 본 그림에서 정사각형이 삼각형의 변을 기준으로 대칭하는 경우다. 이 경우 같은 번호로 대응하는 도형들은 겹친다. (스스로 보여라.) 이 방법은 밖으로 놓인 경우보다 더 쉬어 보인다.

재미삼아 다른 경우도 스스로 해보라. 그런 과정을 해가면서 흥미로운 수학적 사실들을 발견하도록 정신을 바짝 차리기를.

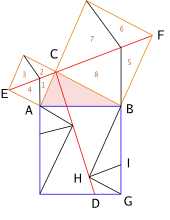
굿헤일 증명

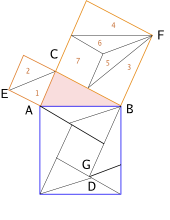
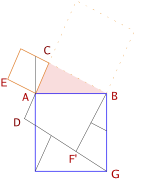
옆의 그림을 보라. 어떻게 작도하였을까?

에프쉬테인의 쪼개기에서 처럼 작은 두 정사각형의 꼭지점을 잇는다.
직각을 이루는 변 중 큰 쪽 정사각형의 꼭지점 F 에서 빗변과 평행한 직선을 긋는다.
바로 앞에서 얻은 선분을 처음 얻은 EF 직선을 기준으로 대칭한다.
나머지는 충분히 유추할 수 있을 것이다.

이 증명의 특별한 점은 과연 무엇일까?

지금까지 본 방법들은 극단적인 경우, 그러니까 직각 이등변삼각형일 경우 어떤 방법이든 같아진다. 더불어 직각을 이루는 변의 길이가 차이가 나면 날수록 위의 방법들은 어떤 차이가 생기는지 상상해보라. 또는 그려보라.

어떤 방법이 더 좋을까?

앞에서 피타고라스 정리를 증명하는 몇가지 방법을 보았는데, 그 중 어떤 것이 가장 좋다고 할수 있을까? 잠깐, '좋다'는 것은 과연 수학적이 말일까? 안될 이유가 없다. (수학적이지 않은 것이 과연 있을까?) 무엇이 더 좋은지 기준을 정할 수만 있다면 이것은 흥미로운 수학적 문제가 될 수 있다. 한발한발 내디뎌 보자. 더 좋은 방법이라고 할 수 있는 조건이 있다면 무엇이 있을까? 여러 기준이 있을 수 있지만, 가장 쉽고 단순한 방법은 좋은 증명이라 할 수 있다. 이 말에 불만이 있더라도 여기서는 잠시만 그렇게 합의하기로 하자. 그렇다면 문제는 더 단순한 방법이란 무엇인지를 정하는 것으로로 바뀐다.

페리갈의 증명이 최선, 회펠의 증명은 최악

어떤 증명이 단순한가를 결정하는 요소도 여러가지 있을 수 있다. 그 중 당장 고려해볼만한 것들은,

보조선은 몇 개인가 ?
쪼개진 도형의 개수는 몇 개인가?

를 생각해볼 수 있다. 따로 보든가 이것들의 합을 보든가. 보조선을 적게 쓰거나 쪼개진 도형의 개수가 많고 적고는 우리에게 무엇을 말해주는 것일까? 쪼개진 도형들이 같다는 것을 보이기 위해 쓰인 '이동(isometry)'의 횟수와 연관이 있다. 하지만, 도형이 작다고 해서 이동의 개수가 작다고는 말할 수 없다. 더 나아가 어떤 이동이 더 단순하고 어떤 것이 더 복잡한가도 아직 답을 기다리고 있다.

눈에 보이기에 단순한 것만 기준으로 하는 것은 어떨까? '대칭성'만 기준으로 삼아 위의 증명들을 다시 보자. 앞의 페리갈의 증명에서 큰정사각형에 쪼개진 부분은 대칭이 완벽하다. 90도 회전할 때마다 그 도형들은 겹친다. 에프쉬테인, 닐슨, 굿헤일의 방법은 부분적으로 대칭이다. 180도를 회전하면 겹친다. 그에 비해 알 나이리찌-회펠의 증명을 보라. 대칭이 아니다, 전혀. 360도를 완전히 회전해야 대칭이 된다. 이런 관점에서만 본다면 페리갈의 증명이 가장 좋은 증명이라고 할 수 있다.

아니! 회펠의 증명이 최선, 페리갈의 증명이 최악

과연 그렇게 쉽게 답할 수 있을까? 이건 어떨까? 증명을 하기 위해서는 결국 쪼개진 조각들이 같다는 것을 보이는 비교 절차가 필요할 수 밖에 없다. 비교할 때마다 도형의 성질에 대한 '정리'들이 쓰일 것이고, 그렇다면 증명하기 위해 공을 얼마나 들였는가로 귀결된다. 그렇다면 여기서 '증명의 단순성'을 재는 기준으로 새로운 것을 제안해 볼 수 있다.

쪼개진 도형의 꼭지점들로 삼각형을 이룰 경우 그 개수는 몇 개일까 ?

모두 볼 필요도 없고 빗변의 큰 정사각형에 담긴 삼각형의 개수만 보는 것으로 충분하다. 지금까지 본 것 중 '알고리듬적으로' 분명하다. 기계가 증명한다고 상상 해보라. 쪼개진 도형을 입력하면 미리 프로그램된 절차에 따라 기계는 삼각형으로 환산하고 작은 정사각형의 조각들과 큰 정사각형의 조각들을 비교하는 정리를 찾을 것이다. 그래서 하나하나 비교해간다.

이 기준으로 위의 방법들을 비교해보자. 에프쉬테인, 닐슨, 굿헤일 증명에서 삼각형 조각은 8개다. 페리갈 증명에서는 ? 그렇다. 10개. 마지막으로 알 나이리찌-회펠 증명은? 7개다. 이 셋 중에서 가장 간단한 방법은 그래서 알 나이리찌-회펠의 것이다.

더 생각해보기

지금까지 호기심을 엮고 풀어온 것을 되돌아보면 흥미로운 사실들이 등장한다. 이런 질문이 가능하다.

최소의 조각은 몇 개 ?

자연스럽게 이런 질문이 생길 수 밖에 없다. 지금까지 우리가 본 증명들 중 쪼갠 조각이 가장 작은 것은 7 개 였다. 그런데 피타고라스 정리를 쪼개기 방법으로 할 경우 이것은 필연적일까 ?

(질문) 삼각형 일곱개 조각이 피타고라스 정리를 쪼개기 방법으로 증명하는 가장 최소의 수일까? 6개 삼각형 조각인 증명이 있을 수 있을까? 5개는 ?

극단적인 경우, 그러니까, 직각이등변삼각형인 경우는 4조각으로도 된다. 이런 경우 말고 일반적인 경우 최소의 수는 몇 개일까? (직접 생각해보라.)

대칭성과 논리성

앞의 결과만 놓고 보면 이런 궁금증이 생긴다. 쪼개기 법으로 피타고라스 정리를 증명했을 때, 논리적으로 가장 단순한 것이 대칭성의 관점에서 보면 가장 복잡했고 그 역도 성립한다. 논리성과 대칭성은 어떤 관계이길래 이럴까? 자연 속에서나 수학 공부를 더 해나갈 때 이와 연관된 문제에 대해 더 많이 생각해보자.

기타

쪼개기 방법은 위에서 열거된 것만 있는 것은 물론 아니다. 다른 방법들도 보면서 위에서 던진 질문들을 다시 생각해보기 바란다.

Note

↑ 당시 유럽은 교부 철학의 영향으로 수학과 과학 연구는 숨이 막혀있었다.

피타고라스 정리 로

[1] 당시 유럽은 교부 철학의 영향으로 수학과 과학 연구는 숨이 막혀있었다.

[1]