Irrational DedekindCut

자연수를 너머로 돌아가기

수의 확장 : 무리수 - 데데킨트 '절단'

앞에서 보았듯이 지금까지 한 어떤 정의도 사실, 실수를 정의하는데 논리적 기초가 튼튼하지 않다. 앞으로 여기서 할 이야기는 현대 수학의 기초를 다진 개념이라고 할 수 있는 집합의 개념 위에서 쌓아올려지고 있다. 그러나 집합론에 대하여 미리 충분히 알아야만 하는 것은 아니다.

17세기 이후 미분적분법이나, 해석기하 같은 수학의 분야가 싹 트고 꽃을 피웠다. 이미 발달한 개념이나 기호표시법과 더불어 오래 걸리지 않아 풍성한 결실을 맺게 된다. 이 분야들의 뿌리가 되는 기초적인 개념이 바로 '무한'과 '연속성'이다. 이 개념들은 우리가 무한 소수점 표현에서 말했듯, 그냥 직관적으로 받아들여졌지만 시간이 흐르면서 그 개념들이 과연 무엇인지 탐구들어지 않으면 안되었다. 연속한다는 것이 무엇인지, 무한이라는 것은 또 무엇인지, 직관적으로 분명해보이는 그 개념들에 대해 논리적인 설명이 필요했다. 사실 앞으로 보아가겠지만 19세기는 수학의 전반에서 이런 일이 종종 일어났다. 누구나 직관적으로 받아들였던 개념들에 대놓고 "너는 도대체 무엇이냐?" 라는 질문을 던지게 된 것이다. 쉽게 믿었던 것을 더 확실하게 믿을 수 있도록 기초를 다지는 시기였다.

이때 그에 답을 했던 큰 수학자들이 등장하는데 그 중 빠뜨릴 수 없는 사람이 바로 독일의 데데킨트다. 그는 대단히 추상적 개념인 '집합'과 집합의 '절단'이라는 개념으로 간단하게 유리수로 부터 무리수를 '생성'(construction)'할 수 있음을 보여 '무리수'의 논리적 기초를 분명하게 하고 아울러 '실수의 연속성'(continuum)을 보인다. 단위들이 계속 나열해가는 연속체(sequence)와 같은 개념으로 실수의 연속성을 설명한 경우도 있지만, 이는 다음 기회에 보기로 한다.

데데킨트 절단의 정의

정의 (집합의 절단) : 어떤 집합 S 를 두 개의 부분 집합 A, B로 나눌 때 다음과 같은 조건을 만족하면 U 를 A와 B로 절단했다고 한다.

$A\cup B=S$
$A\cap B=\emptyset$

하나의 집합을 두 쪽으로 쪼개낸 것이다. 이 개념은 대단히 추상적인 개념이다. 왜냐하면 '어떤' 집합인지 분명하지도 않고 어떻게 나눈다는 것인지도 말하지 않았다. 관심도 없다. 그게 무엇이든 어떻게 하든 쪼갠다는 사실 자체에 집중하여 '어떤' 집합을 '이러저러하게' 나누면 그것을 '절단'이라고 한 것이다. 따라서 이 추상적인 개념은 필요하다면 거기에 더 구체적인 조건을 추가하면서 구체적인 개념을 빚어갈 수 있을 것이다. 여기서는 '실수' 개념의 기초를 다지기 위해 조건을 추가한다. 공기 중에 있는 그 무엇들이 만나 이슬을 맺어 더러 벌레가 빨아먹고 더러 땅에 떨어지듯 모호한 개념들이 더 구체적인 무엇이 되어가는 것을 보게 될 것이다. 데데킨드 절단이다.

정의 (데데킨드 절단) : 원소들의 순서가 정해진 어떤 집합 S를 두 집합 A, B으로 자를 때, 아래의 세 조건을 만족하는 절단을 '데데킨드 절단'이라고 부른다.

A, B 모두 공집합이 아니고
A의 모든 원소가 B의 모든 원소보다 작고
A는 가장 큰 원소를 갖지 않는다.

데데킨드 절단을 집합 기호로 정리해 다시 쓰면,

$A\cup B=S$
$A\cap B=\emptyset$
$\forall a\in A\forall b\in B\ (a<b)$
$\forall a\in A\neg \exists a_{0}(a\leq a_{0})$

물론, 이 정의에서 등장한 집합들은 '순서가 정할 수 있는 집합'이고 모든 원소들이 비교 가능하다는 전제가 깔려 있다. 이에 대해서는 집합 세계 의 순서 있는 집합 을 참고하라.

데데킨트 절단의 예 : 무리수의 존재

예를 보면서 데데킨드 절단이 무엇인지 구체적으로 이해해보자.

예 1 : 유리수 1 인 절단면인 경우.

S:=\mathbb {Q} ,\ A:=\{a\ \in \mathbb {Q} \ |\ a<1\},\ B:=\{b\ \in \mathbb {Q} \ |\ b\geq 1\}

위의 모든 조건을 만족하는 예다. 마지막 조건 'A는 가장 큰 원소를 갖지 않는다'라는 문장도 참이다. 왜냐하면 1 보다 작은 원소를 가진 유리수 집합에서 다른 모든 원소보다 큰 원소는 과연 무엇인가? 만약 그것이 $a_{0}$ 라고 해보자. 그렇다면

{\frac {a_{0}+1}{2}}

라는 수는 분명히 A에 있으면서 $a_{0}$ 보다 크다. 말이 안된다. 따라서 A에는 가장 큰 원소라고할 만한 것을 지정할 수 없다.

이 경우 절단면에 있는 점은 1로 유리수라는 것을 놓치지 않아야 한다. 이런 식으로 정의하면 모든 유리수를 다 정의할 수 있다.

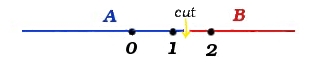
예 2 : 어떤 무리수의 정의

S:=\mathbb {Q} ,\ A:=\{a\in \mathbb {Q} \ |\ a^{2}<2\lor a\leq 0\},\ B:=\{b\in \mathbb {Q} \ |\ b^{2}\geq 2\land b>0\}

위의 기호들을 풀어 정확하지는 않지만 수직선 모델에 나타내보면 ,

이다. 여기서 A나, B는 유리수만 원소로 갖기 때문에 '연속된' 수직선에 나타낸 것은 사실 정확한 표현이 아니다. 그림에서 빨간 점은 제곱해서 2가 나오는 수 중 양수를 뜻한다. 이 수는 A, B 어디에도 포함되지 않는다. 바로 이 수는 우리가 나는대로 유리수일 수 없다. 연속하는 직선의 한 점이면서 유리수와 대응할 수 없는 점이 있다. 유리수는 조밀하지만 아직 연속하지 않다 !

바로 위의 예를 보면, 우리가 정의한 데데킨드 절단의 조건을 모두 만족하고 한가지 특성을 더 갖는다.

절단된 집합 B 에 최소원소가 없다.

이를 일반화해서 '데데킨트 절단'의 두 부분집합 A, B에서,

A 의 모든 원소가 항상 B의 모든 원소보다 작고 A, B 모두 최소원소와 최대원소를 갖지 않는 경우

라고 바꾸어 말할 수도 있다.

이와같이 '데데킨트 절단'을 하면서 절단된 B에 최소원소가 없는 경우 그 절단면인 점에서 우리는 '유리수가 아닌 수'들의 존재를 확인할 수 있다. 유리수들만으로 이루어진 집합들로 무리수의 존재를 확인한 것이다 ! '유리수 집합'은 비록 끝없이 촘촘하지만, 직선에는 유리수와 대응할 수 없는 점이 있다는 것은 여러 방식으로 알 수 있다. 그런데 그런 점이 있다는 사실만 확인했을 뿐, 그것을 채울 충분한 논리적 근거를 갖고 있지 않았다.

데데킨트 절단의 정의를 들여다보면, 순서를 가진 어떤 집합에 대해서도 가능하고 어떻게 나누는가 어떤 기준을 둘 것인가하는 것은 미리 정하지 않았다. 다만 직관적으로 분명한 '집합의 절단' 개념에서 출발한다. '유리수 집합'을 분명하게 제시하고 그게 아닌 것이 무리수라는 방식이 아니다. ${\sqrt {2}}$ 로 쓰는 무리수를 정의했던 위의 예를 보자. 순서 있는 집합의 특수한 경우인 유리수 집합으로부터 정의를 시작했다. 그리고 어떻게 절단하든 상관없이 데데킨드 절단한다. 단, 집합 B에 최소원소가 존재하지 않을 경우 이는 분명히 유리수가 대응할 수 없는 점의 존재를 드러낸다. 그 절단면이 그것이다. 바로 그것이 무리수다. 다른 어떤 외부적인 개념에 기대지 않고 유리수 집합으로부터 무리수의 존재를 드러낸 것이다. 이로써 드디어 우리는 유리수의 모든 점이 수의 직선을 덮을 수 없고 그것을 어떻게 논리적으로 정의해주어야 하나, 그 악몽에서 벗어날 수 있게 되었다. 실수는 모든 데데킨트 절단들 이다.

자연수를 너머로 돌아가기

Note