MathInduction
수학적 귀납 (Mathematical Induction)
자연수 세계는 1, 2, 3, ... 이라는 자연수들과 = , < 같은 비교와 + , * 같은 연산들이 때로는 물처럼 때로는 흐르고 때로는 불꽃처럼 튀며 빚어내는 장대한 드라마다. 그 세계의 비밀을 밝혀내는 것은 멀고 멀어서 끝없이 멀다. 자연수들은 연산으로 서로 어울리는데 비교해 보면서 우리는 어떤 성질을 알아낸다. 그만큼 더 탐험한 것이다. 예를들어
- 1 부터 홀수 n 개를 더한 결과는 그 수를 두번 곱한 것과 같다.
는 성질을 보라. 1 부터 차례로 이어지는 홀수들 n 개의 합이란 n = 1 일 때 1, n = 2 일 때 1 + 3 , n = 3 일 때, (1 + 3) + 5 ... 의 두 수들의 합의 연속을 말한다. 그리고 n 의 제곱이란, n 이라는 수를 두 번 곱했다는 말이다. 그런데 그 결과가 같다 ! 이 성질을 알고 나면 이제 1 부터 홀수 n 개를 더한 결과가 필요한 어떤 과정에서 굳이 더해보지 않고 바로 n 의 제곱을 쓸 수 있다. 그런 성질들을 수학에서는 보통 '정리'라고 부르고 그 정리가 타당하다고 보이는 것을 '증명'이라고 부른다. 그런데 위의 과정은 정말로 모든 자연수에 대해 항상 성립할까?
이 되었다고 해서 n 이 천 개, 만 개 일 때도 될까? 그 보다 더 큰 수에 대해서도 될까 ? 결국 모든 자연수에 대해서 그 성질이 참일까 ? '증명'이란 그 타당성을 설득력있게 말해야 하고 논리적으로 말이 안되는 것은 없어야 한다. 그 말은 어떤 증명이건 타당성을 말하기 위해 더이상 의심할 수 없는 논리적 원칙이 있어야 한다는 것을 말한다. 그 정리가 의심할 수 없는 그 이전에 증명된 성질이나 아니면 더 이상 의심하기 어려운 어떤 기초적 원칙 위에서 논리적으로 밝혀 낸다는 말이다.
예를들어, 위의 성질이 정말 그런지 보자.
- n 이 1 일 때 1 = . 좋다.
- n 이 2 일 때 1 + 3 = . 좋다.
- n 이 어떤 k 에 대해서 위의 성질이 참이라고 하면 반드시 그 다음 단계인 n 가 k+1 일 때도 위의 성질이 참이라고 보이자. 다시말해,
- 가 참이면 도 참이다. (정말 그런가, 확인해보라.)
- 그렇다면 우리가 어떤 자연수에 대해서도 위의 성질이 참이라는 것을 의심할 수 없다. 왜냐하면 n 이 1 일 때, 2 일 때 참이었으니 3 일 때도 참일 것이고 3 일 때 참이었으니 4 일 때도 참일 것이다. 그렇게 계속 가면 99 일 때도 참일 것이고 따라서 100 일 때도 참일 것이다. 아무리 큰 수를 줘도 하나씩 하나씩 단계롤 올려가면 결국 모두 참이다.
위의 증명에 논리적으로 못마땅한 점이 있나? 위와 같은 증명은 자연수 세계의 성질을 증명하는데 자주 등장한다. 위와 같은 방식으로 증명하는데 우리가 딪고 선 원칙을 '수학적 귀납법' (또는 수학적 귀납의 원칙) 이라 부른다. 수학적 귀납의 원칙은 자연수를 관통하는 매우 중요한 논리적 기초다. 자연수 세계에서 증명된 정리가 그보다 확장된 수의 세계인 실수 세계의 성질을 증명하는 데도 응용된다. 그러니 수학적 귀납의 원칙은 수학의 밑바탕에 있는 아주 중요한 주춧돌인 셈이다.
수학적 귀납의 원칙이란 구체적으로 무엇인지 따져들어가기 전에 몸을 풀어 볼 겸 풀어보시길.
- 111 은 3으로 나뉜다. 111111111(1이 아홉개)은 9로 나뉜다. 111...111 (1이 27개)는 27로 나뉜다. 그렇다면 어떤 자연수 n 이라도 상관없이 111...111 (1이 개)는 으로 나뉠까? 아니면 성립하지 않은 어떤 자연수가 있을까 ?
'수학적 귀납의 원칙'이란?

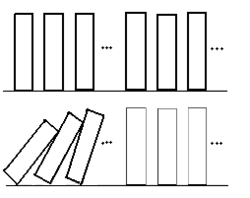
오른쪽 그림을 보자. 끝없이 많은 도미노가 차례로 서 있다. 그러다가 처음 하나가 넘어진다. 그리고 그 다음 도미노가 넘어진다. 어떤 k 번째 도미노가 넘어지면 그 다음 도미노도 넘어진다. 그렇다면 도미노가 모두 넘어진다고 믿을 수 있을까? 과연 그렇다.
- '어떤 것이든' 막대가 넘어어지면 그 다음 것도 넘어진다면, '아, 모든 막대는 다 쓰러지겠구나' 라고 믿을 수 있다.
만약 믿지 않는다면? 그에게 '모든 도미노'가 다 넘어질 것이라는 것을 보이기 위해서는 다르게 설득을 해야할 것이다. 믿지 않은 사람에게 잘못이라고 말할 수는 없다. '넘어지지 않는다' 라고 믿든가 아니면 '넘어질 수도 있고 넘어지지 않을 수도 있다'고 믿을 것이다. 그렇게 믿는 사람들은 아래 글을 더이상 읽지 않아도 된다. '넘어진다'고 믿는 사람들은 이제 다음 문을 열고 자연수의 세계 탐험을 계속해가면서 희열을 느낄 수 있을 것이다.
도미노 처럼 자연수 n 이 1, 2, 3, ... , k, k + 1 이 들어가는 수학적 문장들이 끝없이 있다고 하자.
그럴 때 다음을 보이면 된다. n 이 어떤 자연수건 상관없이 항상 A(n) 이 참이라는 것을 보이기 위해서는,
- 는 참이다.
- 어떤 자연수 k 에 대해서, 이 참이면 도 참이다.
를 보이면 된다. 다시 말하지만, 이와 같은 증명 방식을 수학적 귀납[1]의 원칙이라 한다.
수학적 귀납의 원칙을 쓰기 위해서는 이미 어떤 어떤 성질을 가설로 내세워야 한다. 자연수들 몇 개를 가지고 그럴 듯한 '수학적 가상 실험'을 많이 해본 다음 그것으로부터 어떤 일반식을 '가정'하는 것이다. 그리고 나서 그것이 일반적으로 모든 자연수에 대해 참이라는 것을 보인다. 이것은 수학에서 보통 새로운 정리를 이끌어내는 '연역적'인 방법이 아니다. 그래서 수학적 귀납의 원칙을 과연 증명이라고 할 수 있나 여전히 의심할 수 있다. 그런 분을 위해 한발 물러서서 '검증'(verification)이라고 불러 보겠다. 어쨌든 수많은 정리들이 이 수학적 귀납의 원칙에 발을 디디고 있다.[2] 구체적인 수나 도형으로 특수한 경우들로 '수학적 실험들'을 해 본 다음, 일반적인 법칙을 '추측'하는 사례는 매우 많다. 우리가 처음 든 예도 그렇다. 오일러도 이 방법을 많이 썼던 사람 중 한명이라고 한다. (그러나 역시 이럴 경우 수학적 직관이 문제가 되긴 된다. ) 그래서 나온 '가설'을 수학적 귀납의 원칙을 적용해서 증명 또는 검증을 하면 우리는 그것을 '받아들인다'. 만약 수학적 귀납의 원칙을 써서 증명하지 못했다면 다른 수학적 정리나 논리적 방법으로 증명하기를 기다리면 되는 것이다.
위의 말을 이를 보다 간단히 기호만 써서 나타내 보자.
또는 수리 논리의 기호를 써서
수학적 귀납, 더 자세히 들여다보기
이제 수학적 귀납의 원칙이 무엇인지 느낌이 왔을지도 모른다. 그 '대강'의 것을 더 정밀하게 들여다보자.
수학적 귀납의 일반화된 형태
우리는 수학적 귀납의 첫단계로 자연수 1 부터 시작했지만, 물론 그렇지 않아도 된다. 모든 자연수에 대해서 보기 위해서 그랬던 것일 뿐이다. 어떤 자연수의 부분인 s, s+1, s+2 , ... 에 대한 성질을 보고 싶다면 가장 작은 수 s 에 해당하는 수학적 문장 A(s) 이 참이라는 것부터 시작하면 된다.
임의의 자연수 s 에 대해 다음의 수학적 문장들이 있다고 해보자.
- A(s), A(s+1), A(s+2), ... , A(k), A(k+1),
그럴 때,
- (base) A(s) 가 참
- (step) s 보다 큰 모든 k 에 대해, A(k) 이 참이면, A(k+1) 도 참이다.
그렇다면 s 보다 큰 모든 n 에 대해 A(n) 도 참이다.
수학적 귀납은 정리인가? 그냥 믿어야 할 건가?
수학적 귀납의 원칙은 증명할 수 있는 '정리' 일까? 아니면 그냥 '믿어야 할까'. 우리는 앞에서 '믿음'을 전제하고 말했지만, 언뜻 보면 수학적 기호로 표시할 수 있는 문장이니 이것도 더 기초적인 어떤 원리에 따라 증명할 수 있지 않을까 생각해볼 수 있다. 그러나 그렇지 않다. 그것은 하나의 '원칙'이며 약속이다. 앞에서 라는 문장에서 수학적 문장 이 무엇인지, 아직 알 수 없다.
이렇게 말하는 사람도 있다.
- 아니, 가 무엇이건, base 인 가 증명되었고, step 에 따라, 이 증명된 것으로 볼 수 있으니, 도 증명된 것 아니냐. 이제 다시 step 에 따라 도 증명된 것이고, 따라서 도 증명된 것이다. 이런 식으로 계속 차근차근 해가면 결국 어떤 자연수 n 에 대해서도 이 증명 되었다고 볼 수 있다. 그렇다면 우리는 수학적 귀납원칙이 증명되었다 고 볼 수 있다.
하지만, 이 논리를, 수학적 귀납의 원칙을 증명하는데 그 안에 '수학적 귀납의 원칙'을 쓰고 있다. '계속 차근차근 하다보면 모든 자연수에 대해서 된 것과 같다' 라고 한 부분이 바로 그 부분이다.
수학적 귀납의 원칙을 써서 증명한 사례는 16세기 후반에 최초로 발견되었다. 우리가 처음에 든 홀수들의 합에 대한 예가 바로 그것이다. 그리고 자연수 세계의 기초를 공리 체계로 만든 Peano 체계에 공리로 들어가 있다. 그렇지만, 공리란 '믿기로 한 약속'들이기 때문에, 그것을 믿으면 그 체계 위에 수학의 집을 지으면되고 그것을 믿지 않으면 다른 기초 위에 지으면 된다. 수학적 귀납의 원칙을 받아들이지 않아도 좋다. 그러나 그 댓가를 톡톡히 치러야 한다. 자연수 세계의 성질을 증명하는 것이 '매우' 어려워 질 것이 분명하다. 그리고 그 성질을 기초로 증명한 다른 모든 수학적 성질을 받아들이지 않아야 한다. 수학적 귀납의 원칙이 없는 수학체계는 매우 복잡하고 따라서 증명된 문장이 현저하게 줄어들 것이며 따라서 아주 '빈곤한' 수학이 될 가능성이 크다.
그런데 다른 한편 수학적 귀납의 원칙은 증명된다. 이게 무슨 소리인가? 증명 안된다고 해놓고 또 증명이 된다니?
자연수 세계에는 또다른 중요한 원칙이 있다. 바로 최소 원소의 원칙(Principle of the smallest integer)이라는 것이다.
- (최소원소의 원칙) 공집합이 아닌 어떤 자연수의 부분 집합에도 최소원소가 있다.
이 최소원소의 원칙을 받아들인다면 우리는 수학적 귀납을 증명할 수 있게 된다 ! 이 원칙은 이건 너무나 당연한처럼 보인다. 믿고 말게 뭐 있단 말인가. 누구나 의심할 수 없는 것 아닌가. (과연 그런가?) 그렇게 분명한 원칙에서 수학적 귀납의 원칙을 증명할 수 있다니, 그렇다면 최소 원소의 원칙이 더 밑바탕에 깔린 주춧돌이라고 여길 수 있다. 그럴까 ? 결론부터 말하면, '아니올시다' 이다. 왜냐하면, 입장을 바꾸어서 수학적 귀납이 원칙으로 받아들일 때 최소 원소의 원칙을 증명할 수 있기 때문이다. 묘하지만 그렇다. 말로 표현되기로는 두 원칙이 하늘 땅 만큼이나 달라보이지만, 논리적으로는 거의 등가인 셈이다. [3]
- 최소 원소의 원칙(SI)을 믿는다면, 그것을 지렛대 삼아 수학적 귀납의 원칙(MI)이 옳다고 보일 수 있다.:
|
- 우리가 수학적 귀납의 원칙(MI)을 믿는다면, 최소 원소의 원칙(SI)이 참이라는 것을 보일 수 있다 :
|
잘 되었다. 자연수 세계에서 어떤 성질에 대해 우리가 증명하고자 한다면 수학적 귀납이건 최소원소의 원칙이건 편한 것으로 증명에 적용하면 된다. 아래의 문제들을 풀면서 이를 확인해보자.
수학적 귀납 : 조심 !
수학적 귀납 원칙을 만만하게 보다가 함정에 빠질 수 있다.
(예 1[4])
- 모든 말은 같은 색이다.
여기서는 A(n) 을 'n 마리의 말은 같은 색을 가지고 있다. ' 로 정의한 것이다.
|
(예 2[5])
- 1 보다 크거나 같은 임의의 두 자연수는 같다.
|
앞의 예제와 다를 것 없는데, 여기서는 더 '꼬아놓았다'. 어디가 잘못인가?
수학적 귀납법이 쓰여 증명할 수 있는 중요한 문제들
아래에는 수학의 다른 분야에서 기초적인 정리로 매우 중요한 역할을 하는 정리들이다. 이것들은 수학적 귀납의 원칙을 써서 어렵지 않게 증명할 수 있다. (수학적 귀납의 원칙을 쓰지 않는다면 ?)
- p > -1 인 모든 수 p에 대해 그리고 1보다 크거나 같은 자연수 n에 대해[6]
이것을 증명하면 해석학의 가장 기초적인 정리인 다음을 쉽게 증명할 수 있다.
- -1 < q < 1 인 모든 q 에 대하여,
- 뉴튼의 두 항의 곱들에 대한 정리 (Binomial Form)
여기서 !
다른 흥미로운 문제들
수학적 귀납의 원칙을 적용하는 문제들 모음을 참고하라.
Note
- ↑ 그런데 왜 '귀납(induction)'이라는 말을 썼을까? '귀납'(induction) 이란 다양한 특수한 예로부터 일반적 법칙을 끄집어 내는 사유방식을 일컬을 때 쓰는 용어다. 수학적 귀납의 틀을 보면 나 과 같이 특수한 경우의 수학적 문장들을 증명하여 라는 일반적 진리를 유도한다는 점에서는 유사하다. 다만 과학에서는 실험과 관찰을 반복하면서 종합하고 일반적인 법칙을 유도하는 반면, '수학적' 귀납은 ' '이라는 '논리적 연계성'을 보임으로써 '모든 n 에 대하여 ' 이라는 수학적 문장(성질)들이 참이라는 것을 보인다는 점에서 다르다.
- ↑ 수학에서 '귀납적 방법'들의 사례, 역사에 대해서 자세히 다룬 책이 있다. 헝가리 출신의 유명한 수학자 포이야(Pólya ; 1888-1985)의 유명한 책 How to Solve It, Mathematics and Plausible Reasoning
- Volume I: Induction and Analogy in Mathematics, and Mathematics and Plausible Reasoning
- Volume II: Patterns of Plausible Reasoning. 을 참고할 필요가 있다.
- ↑ 여기서 '거의' 라고 여운을 두는 이유는 있다. 이에 대해 미묘한 분석이 필요하다. 최소원소의 원칙에 쓰인 용어들은 집합론의 용어들이다. 집합론적으로 최소 원소의 원칙이 통하는 집합을 '잘 순서지워진 집합'이라 한다. 자연수 집합은 그렇다고 받아들이는 것이다. '잘 순서지워진 집합'에 대해서는 순서 지워진 집합 을 참고하라.
- ↑ 포야이의 'how to solve it' 에 담긴 예제
- ↑ WIM 에서 인용
- ↑ 위의 수학적 문장은 약간 '세게'해 볼수 있다 : p 와 n 을 엄격하게 적용할 경우, 아래와 같이 두 항의 관계를 더 엄격하게 할 수 있다.
- p > -1 고 0 이 아닌 모든 수 p 에 대해 그리고 2보다 크거나 같은 자연수 n 에 대해
- p > -1 고 0 이 아닌 모든 수 p 에 대해 그리고 2보다 크거나 같은 자연수 n 에 대해
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia













![{\displaystyle (A(1)\land \forall k[A(k)\rightarrow A(k+1)])\rightarrow \forall nA(n).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa0673839f6ff2bb7a2186ad0c56fe2c63fcc48c)




















