MPR Intro
서문
이 책의 목적은 수학 공부하는 사람과 수학 교사를 돕는 것을 목표로 합니다.
두가지 사고 유형 : 엄격하게 증명함과 그럴만한 짐작
엄격히 말해서, 수학뿐만 아니라, 다른 것에 대해서도, "안다"고 하는 것은 문장으로 이루어져 있습니다. 그 중 아주 믿을만한 문장이 있고 덜 믿을만한 문장도 있습니다. 보통 수학적 문장은 증명할 수 있는 문장이고 증명된 문장입니다.
- 수학은 치밀하고 엄격한 논리가 적용되어 적용된 문장들이라고들 생각합니다.
이런 증명된 문장은 의심이나 논쟁할 거리가 별로 없는 아주 믿을만한 문장입니다. 하지만 모든 문장이 꼭 그렇게 매우 믿을만한 문장으로 되어있지는 않습니다. 수학에서도 마찬가지입니다. '그럴만하겠다'(plausible reasoning) 는 방식으로 생각하는 것이 그런 것입니다. 이런 생각은 따라서 꼭 맞다는 보장도 마땅하지 않고 논쟁의 여지가 있습니다. 하지만,
- '그럴만하겠구나.' 하는 방식으로 추론을 하는 것도 지식을 넓히거나 더 단단히 합니다.
수학 공부를 '엄격하게 증명하는 사고'를 배우는 것으로들 알고 있습니다. 이것은 오로지 증명들과 엄격하게 증명할 문장들로만 이루어진 것으로 '이미 완결된 수학'이라는 생각을 하게 됩니다. 엄격하게 증명하는 데서 중요한 것은 '그럴듯한' 것을 엄격하게 근거가 있는 것으로 분명하게 보이는 것입니다. 하지만, 이것은 수학공부가 가진 하나의 양상일 뿐입니다. 수학 공부를 통해서 그런 태도도 기를 수 있지만 마찬가지로 '아 그렇다면 이렇게도 되겠구나' 하면서 지식을 확장해가는 '짐작하기'도 배울 수 있습니다. 여기서 짐작하기도 마냥 아무 생각이나 하는 것이 아니라, '그럴만하게 타당한' 것을 추리해가는 것입니다. 더 그럴만한 것으로 덜 그럴만한 것을 대체해갑니다. 그래서 이 둘 사이엔 모순이 없습니다. 서로 보완적입니다. 정말 수학을 잘하기 위해서는 '짐작해보기'도 잘할 줄 알아야 합니다. 이것은 '창조적'인 일과 연관되어 있습니다. 어느 정도 알고 있을 때, "자, 그래 그럼 여기서 여러분 같으면 어떻게 하겠어요?" 하고 물어보는 식입니다.
이 책의 구성
그렇다고 "어떻게 짐작할 것인가?" 에 대한 분명한 방법이 있는지는 저도 모릅니다. 그래서 이 책은 그렇게 생각할 수 있는 사례를 다룹니다. 여기서 다룬 수학적 발견의 사례들이 꼭 그랬다는 것은 아닙니다. 정확히 역사적으로 사실을 따른 것은 아닙니니까요. 그런 발견을 했을 때, 그럴 만했겠구나 하고 생각되는 흐름을 따라간 것입니다.
단원이 끝날 때는 사례와 참고 사항을 달았습니다. 참고 사항은 복잡하거나 매우 민감해서 본문에서 다루면 지엽적인 문제가 되거나 곁가지로 빠질 수도 있는 내용들입니다. 사례는 더 많은 사람이 이 책을 읽을 수 있도록 하기 위해 기초적인(elementary) 것을 실었습니다. 하지만 꼭 그렇지 않은 것들도 있습니다. 수학사적으로 의미있는 발견이고 수학의 아름다움을 느끼거나 다른 학문 분야나 일상에서 연관이 있는 것들을 예로 들었습니다.
엄격한 뜻에서는 아니지만 실제로 현장에서 적용한 결과를 바탕으로 이 책을 구성한 곳이 많습니다. 이 책에서 보는 문제들은 실제 강의에서 여러 그룹들에게 적용해본 것입니다. "그럼, 여기서 어떻게 될까?" 하고 물은 적이 꽤 있고 그것에 대한 반응들이 이 책에 반영되기도 했습니다. 여러분도 그 자리에 있었던 것처럼 해보기 바라는 마음이었습니다.
물론 이 책에 예로 든 것들을 꼭 그 목적에 한정짓지 않아도 됩니다. 철학적인 문제로 진지하게 다루어도 될 것입니다.
How to solve it ? 의 연장인 이 책은 두 권으로 되어 있지만, 서로 독립적입니다.[1]
제 1 장. Induction (귀납)
Induction [2] (귀납)은 그럴만하겠구나 방식으로 생각하는(plausible reasoning) 방식의 하나의 대표적인 예다. 비슷한 예들을 모아서 보니, 지금까지 이랬으니 그 다음 것도 그럴 만 하겠구나 라고 가정한다. 그리고 그것을 검증(실험) 하는 방식으로 실제로 그런지 아닌지를 조사해보는 방식이다.
- 수학에서도 구체적인 사실들을 관찰해서 그것으로부터 새로운 사실을 발견해가곤한다. 관찰에 상당한 의미를 부여하는 것은 모순적인 말로 들린다. 왜냐하면 보통 관찰이라는 것은 '느낌'으로 받아들이는 물리적 현상들에 대해서 적용하는 말인데, '수학의 대상' 은 관찰할 수 있는 것이 아니고 우리의 '순수한 이성'의 산물일 뿐이기 때문이다. 하지만 실제 새롭고 흥미있는 수학적 사실을 발견할 때 우리는 종종 지금까지 발견된 사실들을 관찰하고 그것들을 종합해서 induction 의 방법으로 새로운 사실을 이끌어내기도 한다. 물론 관찰해서 induction으로 짐작하고서 무작정 그 사실이 옳다고 주장할 수는 없다. 잘못된 경우도 많다. 중요한 것은 그런 방식으로 유추하고 난 다음 새로 발견된 성질이 정말 옳은지 신중하게 검토해서 그것을 증명하거나 반증해야한다는 점이다.[4]
우리는 흔히 경험(실천)으로부터 배워가고 있고, 또 그래야한다. 경험(실천)으로 어떤 사실들을 이해하고 받아들이며 그것을 종합해서 우리 마음 속에 표상을 이루고 또는 잘못된 생각했던 것을 바꾸기도 한다. 그렇기 때문에 '올바로 이해하기 위해서' 경험하는 것은 매우 중요하다. 경험(실천) 속에서 어떤 새로운 문제를 던지는 것은 사람다움의 중요한 특질의 하나이다. 문제가 만들어지고 나면 연구자들은 문제를 가장 적합하게 해결하기 위해 애쓴다.
induction 의 사례 : 골드바흐 추측
경험으로부터 이해하는 방법이 바로 induction이다. 보통 수학은 가장 deductive 한 체계라고 이해하는 경향이 있지만, 세상을 이해하고 표상하는 가장 기본적인 방법인 induction은 수학의 발견에서도 예외가 아니다. 새를 연구하는 사람들이 새에 대해 새로운 지식을 얻고 싶다고 하자. 의미있고 흥미로운 결과를 얻기 위해서는 먼저 이에 대해 어느 정도 알아야 하고 애정을 가지고 관찰을 하게 될 것이다. 수학에서도 마찬가지다. 수를 가지고 놀다가 우연히 이런 경우와 부딪혔다고 하자.
이런 세 관계를 통해 우리는 어떤 질문을 하게 될까? 어떤 규칙성이 숨어 있는 것 같다. 무엇일까? 이것을 추론하는데 거창한 지식이 필요한 것은 아니다. 자연수를 분류하는 방식에 대해 조금만 알고 있으면 된다. 짝수와 소수를 알고 있다고 하자. 왼쪽은 모두 소수들 두 개의 합이고 오른쪽은 짝수다. 이런 현상은 특수한 현상일까? 궁금하니 짝수 6, 8, 12 들을 더 보자.
역시 문제가 없다. 이렇게 특수한 수들을 그것들을 연산해보고 어떤 현상을 추측한 다음 더 많은 다른 수에도 적용해보면서 같은 결과가 나온다면 처음 던진 추측이 옳았다는 쪽으로 점점 기운다. 앞의 사실에서는 이런 사실을 '끄집어내기 (induction)' 할 수 있다.
- 4보다 큰 짝수는 모두 두 홀수 소수의 합으로 나타낼 수 있다. 또는
- 소수도 아니고 어떤 소수의 제곱도 아닌 모든 짝수는 두 홀수 소수들의 합으로 나타낼 수 있다.
문장 2는 문장 1 보다 조금 까다롭고 금방 떠오르지 않을만한 가설이긴 하다. 어쨌든 두 사실 모두 우리가 바로 믿어비리기엔 아직 이르다. 수를 조금 더 해보자. 예를들어 60도 그렇게 나타낼 수 있을까? 3 에 더해서 60을 만들 소수는 없다. 다음 소수 5를 더해도 안되기는 마찬가지. 그렇다면 7 에 대해서는 ? 그렇다 !
로, 두 홀수 소수의 합으로 나타낼 수 있다. 우리가 던진 가설을 뒷받침해주는 사례를 더 찾았다. 하지만 여전히 문제는 남는다. 모든 그런 짝수에 대해서 그것이 성립하리라고 말하기는 어렵다. [5]바로 이 사실을 증명할 수 없다고 해도 너무 실망하지 말기를. 이 말을 처음한 골드바흐(Goldbach) 이래 지금까지 이것은 분명하게 증명되지 않았다.[6]
induction : 학문하는 태도
어쨌든 위에서 했던 방식으로 새로운 사실을 추측하는 것을 Induction 이라 한다. 현상을 유심히 들여다보고 얻은 관찰로부터 임시로 가설을 내고 그것들을 검증할만한 다른 구체적인 사실들로 뒷받침하여 가설을 다듬어가면서 새로운 사실을 이해하고 표상하는 방식이다. 사람이란 본디 영혼의 평정을 깨고 싶어하지 않으려 하기 때문에 환상(착각, 오해 illusion)을 갖고 한번 가지면 잘 버리려고 하지 않는다. 하지만 그것은 학문하는 태도가 아니다. 학문은 앞에서처럼 induction의 방식으로 새로운 사실을 깨닫고 계속 검증해간다. 이 방식은 세계를 이해한 표상을 구체적인 경험(실천)에 견주게 검증한다. 그리고 뒤에 말다툼할 여지를 미리 없애도록 요구하며 가능한 한 일반화시켜 어떤 현상을 이해하고 다시 그것을 가장 구체적인 사실에 견주도록 한다.
이 방식은 요구한다.
- 모든 가능성을 열어두고 검토하라. (이성의 용기-씩씩함) 아리스토텔레스이래 가져왔던 물리법칙과 그의 권위와 동시대인들의 편견에 맞서 실험으로 새로운 물리학 연구의 시대를 연 갈릴레이를 보라.
- 잘못이라서 바꾸어야만 하는 상황이면 바꾸어라. (이성의 참됨-정직성)
- 충분한 검증없이 잘못되었다고 함부로 바꾸지 말아라. (현명한 절제)
이것을 요약해서 말하면 이렇게 말할 수 있을 것이다 : 모든 것을 함부로 믿지 않되 의혹을 일으키는 것이 분명하지 않으면 함부로 의심하지 말라. 이 세 특성은 학자가 가져야할 기본적인 도덕성이라 할만하다.
제 2 장 : 일반화, 특수화, 유추
케플러가 '나의 최고의 스승은 유추(analogy)다' 라고 말했듯 어떤 구체적인 사실들로부터 새로운 사실을 이끌어내는 데(induction) 있어, '유추해보기'는 큰 힘을 발휘한다. 여기서는 induction과 연관된 구체적인 방식인 일반화, 특수화, 유추에 대해 알아본다. 이 세 방식으로 우리는 '기초적으로 알고 있는 지식'들로부터 가장 기본적인(fundamental) '사고의 연산(operation)'을 통해 어떤 특성을 뽑아내어 (induction) 새로운 사실을 알아내거나 검증해 갈 수 있다. [7]
일반화와 특수화
일반화란 어떤 부분집합을 관통하는 성질이 그 집합을 포함하는 더 큰 집합에 적용할 때 이르는 말이다. 그 반대의 경우가 특수화다. 예를들어 보자.
- 어떤 3각형들의 집합에 대해 어떤 성질을 알아보고 그것이 갖는 어떤 성질이 n각형에 대해서도 성립하는지 본다.
- 0도에서 90 사이의 각에 대해 삼각함수의 일반성질을 각의 제한없이 어떤 각에 대해서도 성립하는지 본다.
이런 경우를 일반화라 하고 그 반대의 경우가 특수화다. 이것들이 일반화(특수화)의 대표적인 두 방향이다. 첫번째는 상수 3 에 대해 적용했던 것을 변수 n 에 대해 보는 경우고 두번째는 어떤 제한적인 범위 안에서의 변수에서 제한이 없는 변수로 확장하였다.[8]
유추
유추(유비) 란 어떤 두 대상(또는 집합)의 닮은 점에서 어떤 새로운 사실을 끄집어내는 방식이다. 닮은 점을 끄집어내어 나타낸다고 해서 모두 유추는 아니다. 어떤 시인이 여인과 꽃을 비유했다고 하자. 시인의 감수성은 그 두 대상의 어떤 닮은 점을 끄집어 나타내긴 했지만, 어떤 분명한 개념으로 포착한 것이 아니다. 이렇게 어떤 대상들에 대해
- '정의할 수 있는 어떤 분명한 개념'으로 유사성을 포착해내면 유추라고 부르기로 한다.
더 정확히 말해볼까? 어떤 두 대상이 있을 때, 그것들이 갖는 부분들이 대응하고 그 대응이 어떤 분명한 개념으로 상응하는 경우다. 예를들어, 2차원 평면에서 삼각형과 3차원 공간에서 사면체 사이에는 분명한 유사성이 있다.
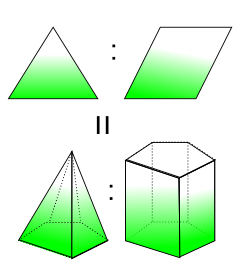
- 하나의 평면에서 직선 둘 로는 어떤 닫힌 도형을 이룰 수 없지만, 셋 으로 이룰 수 있고 그것이 삼각형이다.
- 하나의 공간에서 평면 셋 으로는 어떤 닫힌 도형을 이룰 수 없지만, 넷 으로는 이룰 수 있고 그것이 사면체다.
유추(유비)의 개념은 그리스어 비례(propotion)에서 왔다는 사실로부터 유추(유비)의 개념을 더 잘 이해할 수 있다. 두 원소 6 과 9로 이루어진 시스템 {6,9} 은 다른 시스템 {10,15} 와 비례하는 성질이 있다.
오른쪽 그림에서 보듯 도형의 세계에서도 이런 예를 찾아볼 수 있다.
- 삼각형 : 사각형 = 각뿔 : 각기둥
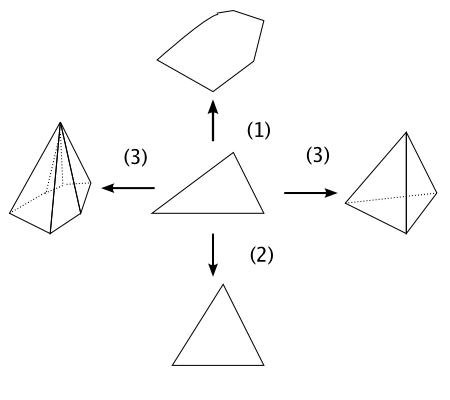
일반화, 특수화, 유추의 관계를 잘 보여주는 예가 아래 그림에 있다. 이 경우 (1) 관계는 보통의 삼각형에서 n 각형으로 확장해서보는 '일반화', (2)는 정삼각형이라는 더 특수한 경우에 적용해보는 '특수화', 그리고 (3)은 그것을 공간으로 확장해서 비슷한 성질을 보는 유추(유비)를 말한다.
사례 : 피타고라스 정리
일반화, 특수화, 유추의 방식은 구체적인 수학 문제를 해결하는데도 실질적으로 도움을 주기도 한다. 유명한 피타고라스 정리 다. 왼쪽의 그림은 유클리드 'Elements'에 나오는 문장 중 우리에게 가장 익숙한 형태의 도형 작도다. 이것은 직각삼각형의 빗변이 a 고 나머지 두 변이 b, c 일 때,
관계가 참이라는 것을 말한다. 그리고 오른쪽 위의 그림은 그것의 일반화한 성질을 말한다. '직각삼각형의 세 변에 상응하는 변에 닮은 도형을 작도할 경우 빗변에서 이룬 도형의 넓이는 다른 두 변에서 이룬 두 도형의 넓이들의 합이다.' 라는 것으로 대수식으로 간단히 나타내면, 변에 이룬 도형에 따라, 아래 성질을 참이게 하는, 어떤 양수 k 가 있다는 말이다.
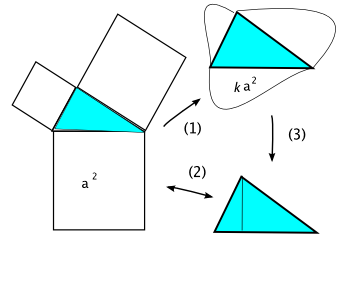
이 경우, 앞의 설명이나 그림에서도 분명하게 알 수 있듯이 (1) 은 일반화를, (3)는 비례한 도형이 다시 직각삼각형이고 '안으로접은' 특수화를 (2)는 유추(유비)를 말한다. 흥미로운 것은 피타고라스 정리가 정립하면 그 일반정리가 성립하기도 하고 그 역도 성립하므로 왼쪽 그림같은 특수한 경우와 오른쪽 위의 그림의 일반적인 경우가 논리적으로 상호등가라는데 있다. 물론 이것을 설명하기 위해서는 닮은 도형들의 상응하는 변이 a : b : c 일 때, 그것으로 이룬 넓이의 비는 라는 사실만 알고 있다면 충분하다. 따라서 직각삼각형의 변에 올린 특수한 어떤 도형 하나에 대해서 아무것이나 보이면 일반적인 경우도 성립하고 그래서 '보통의' 피타고라스 정리도 성립한다. 이 사실을 보이는 데는 오른쪽 아래의 그림과 '비례'에 대한 기초적인 정리면 충분하다.[9]
사례 : 오일러의 무한수열의 합
비슷한 것에 적용해서 보는 유추 방식은 모든 새로운 발견에 어김없이 어떤 역할을 하고 있기 마련이다. 이제 볼 사례는 그런 것 중 아주 의미있는 사례다. 무한 수열의 합에 관한 오일러의 발견이다. 스위스의 야곱 베르눌리(Jacob Bernoulli ; 1652 - 1705) 는 무한 수열의 합을 여럿 찾았지만 아래 무한 수열의 합은 도무지 찾을 수 없었다.
- .
이 문제를 해결한 것이 야곱의 동생 요한 베르눌리(Johann Bernoulli ; 1667 - 1748) 의 한 때 제자였던 레오나르드 오일러(Leonhard Paul Euler ; 1707 - 1783 ) 이다.
오일러는 당시까지 증명되지 않은 성질을 과감하게 받아들여 사용하였다. 당시 차수가 n인 대수방정식의 해의 개수와 인수 분해 문제는 아직 완결된 문제가 아니라 논쟁과 발견 중이었다. 그런데 유한 차수인 n에 대해서도 그랬던 이런 류의 문제를 항이 끝없는 방정식에 도입한 것이다. 그 방식이 스스로 생각해도 수학적으로 엄밀하게 증명이라고 할 수 없다는 것을 알고 여러 방식으로 검토했다. 어려 해가 흘러 이 문제로 다시 돌아와 다시 점검하고 더 나은 증명을 꾸준히 시도했다. 그가 했던 방식을 보면서 자세히 알아보기로 하자.
먼저, 당시 알고 있는 사실과 그것으로부터의 유추 : n 차 대수방정식
은 n 개의 서로 다른 근
을 갖는다면, 왼쪽의 다항은 1차식의 곱셈으로 아래 오른쪽 항처럼 달리 나타낼 수 있다. [10]
이제 오른쪽 항을 풀어내어 근들과 차 항의 계수를 비교하면 아래의 식이 성립한다는 것은 분명하다.
이와 같은 전개과정을 흔히 쓰이던 것인데, 이것을 살짝 비틀어 다르게 표현할 수도 있다. 어떤 근도 0 이 아니라면
이고 근들과 x 의 계수를 비교하면 아래 식도 참이다.
이제 대수방정식의 특수한 형태를 보더라도 이 일반적인 원리는 그대로 적용될 것이다. 우리의 관심은 양수 제곱항들이 분모로 있는 무한 수열의 합 이었다. 이것에 가까이 가기 위해 특별한 경우를 본다. 다름아닌 짝수 차수에 부호가 바뀌어가는 대수방정식이 바로 그것이다. 그렇게 하기 위해, 대신 을, 대신 가 짝수면, 를, 가 홀수면 로 바뀐 경우, 위의 '조건'들이 모두 만족한다면 , 근은
- 또는 다.
앞에서 했듯이 항의 계수를 이 근들로 표현하면,
이 된다.
준비는 끝났다. 여기까지 밀어붙인 오일러는 다음 '무한 개의 항을 갖는' 식에 위의 결과를 적용한다. 먼저 다음에 주목한다. [11]
이 방정식의 근들은
다. 여기서 위에서 '근이 0이 아니고 서로 다르다면' 이라는 조건을 만족시켜야 하므로 0을 버리면 바로 앞의 특수한 경우와 매우 비슷해진다. 그래서 양쪽 항을 모두 x 로 나누면,
꼴이 되어 근은 0이 뺀 나머지들이다. 그 '유사성' 을 그대로, 과감하게, 적용하면, 앞에서 은 1, 은 , 은 , 은 , ... 이 된다. 그래서 결국
이 되어 야곱 베르눌리가 찾고 싶었던 바로 그 등식이 마침내 나오게 된다 !
오일러는 이렇게 발견한 사실이 엄격한 증명이 아니라는 것을 스스로 알고 있었다. 하지만, 유한개의 함수열에 적용했던 것을 마찬가지로 무한개의 함수열에 적용한 것이 완전히 잘못된 것은 아니라는 것을 '검증' 해간다.
- 그가 다른 방법으로 야콥 베르눌리의 수열에 대해 찾은 7 숫자로 정확히 찾은 값(1.644934)이 나오는지 본다. 문제가 없었다.
- 더 많은 자리수까지 정확히 계산한다음 이 정리를 적용해서 검증한다. 역시 문제가 없었다.
- 네제곱수들을 분모로 갖는 무한 수열의 합도 구해봐도 마찬가지였다.
- 라이프니쯔가 찾은 놀라운 식[12]에도 앞에서 했던 방식을 그대로 적용해본다. 대신 이때 적용한 방정식은 이고 그때 근은
다. 역시 문제 없었다. 다른 방식으로 라이프니쯔가 찾은 결과와 같았던 것이다 !
- 계속 증명을 시도하여 새롭고 논리적으로 더 엄밀한 방법을 찾는다.
오일러의 사례를 통해 우리가 하는 논의에 견주어 주목해야할 부분들은 분명하다. 위의 사례를 보면서 이미 짐작했겠지만, 오일러는 새로운 사실을 발견해가는데, 무모하리만큼 용기있는 태도로 induction의 방식을 관철하고 있다 : 일반화, 특수화, 유추(유비) 의 방식들을 자유자재로 써서 새로운 사실을 끄집어 내고 그것을 검증하고 있는 것이다.
Note
- ↑ 이 책의 2권 "개연 추론의 틀"(그럴만하다고 짐작해가는 추론의 틀) 은 주로 논리, 통계적 사고를 다루고 있다.
- ↑ 학문적 용어로 Induction 은 많은 유럽 나라들이 비슷하게 쓰는 말이다. 중국어 한자권에서는 귀납(歸納) 으로 흔히 쓰인다. 이와 상대적인 말로 보통 deduction이라는 말이 있다. 연역(演繹) 이다. 이런 말은 일상에서 보통 쓰지 않기 때문에 선뜻 이해가 되지 않는다. 어떤 구체적인 사실들을 관찰해서 지금까지 그래왔으니 그런 비슷한 이 성질도 그럴 것이다라고 유추하는 논리를 펴는 것이 귀납이고 참이라고 생각하는 기초적인 전제들로부터 엄격한 논리 규칙에 따라 새로운 성질을 밝히면서 유추하는 방식이 연역이다.
- ↑ 이 부분은 꽤 의역했음. :-)
- ↑ 여기서 증명과 반증의 뜻이 모호하다. 상대적으로 현대적 학문인 수리논리학적 관점으로 볼 때 증명은 어떤 공리에서 엄격한 논리의 절차를 밟아 새로운 사실을 이끌어내는 것으로 대단히 연역적인 개념이다. 하지만, 이런 엄격한 관점 만이 옳다고 말할 수는 없다. 어떤 이들은 '증명'이란 결국 '설득과 납득' 아니냐고 하는 사람들도 있다.
어떤 관점을 갖든, 여기서 오일러가 한 말에서 중요한 물음 한가지가 생긴다. 먼저 반증의 뜻을 다시 보자. 반증이란, 그 문장을 부정할 근거를 확실히 밝히는 것이다. 어떤 문장 P를 반증하다는 것은 'P 가 아니다'를 증명하는 것과 같다. 바로 이것이다.
- "어떤 수학적 사실이 있다고 하자. 그것이 어떤 뜻에서 참이라고 하자. 그렇다면 우리는 항상 그것을 증명하거나 반증하거나 둘 중 하나일까?"
- ↑ 이런 식으로 믿음을 뒷받침하는 것은 문제가 아주 많다는 것은 분명하다. 짝수가 커질수록 우리는 그것을 나타낼 수 있는 두 개의 소수를 찾는 것이 놀랍도록 어려워진다. 어쩌면, 이것은 소수 본연의 모습이다. 소수 세계는 쉽게 자신의 비밀스러운 세계를 드러내지 않고 있다. 아직까지 어떤 자연수를 구성하는 소수를 찾는 문제는 수학에서 가장 어려운 분야다. 이에 대해서는 소수의 분포 와 그것과 이어진 부분들을 참고하라.
- ↑ 이 가설의 역사와 현대적 성과에 대해서 골드바흐 가설 을 참고하라.
- ↑ g 가 일반화라는 사고 연산, s 가 특수화라는 사고 연산, 그리고 a가 유추(유비)라는 사고연산이고, x들이 이미 알고 있는 어떤 지식들, 이라면 앞에서 한 말을 식으로 나타내면 라고 할 수 있을까? :)
- ↑ 사실 이것을 두 방향이라고 할 수 있겠나? 어떤 '제약 조건'에서 제약하는 조건을 풀어가는 하나의 경우로 볼 수도 있다.
- ↑ 이에 대해서 보충 설명은 피타고라스 정리의 일반화를 보라.
- ↑ 보통 대수의 기본법칙 이라고 불리는 정리와 비교해보라. 대수의 기본 정리 를 참고하라.
- ↑ 이 사실은 누가 발견한거지? 나중에 무한수열의 수렴성과 그 성질, 테일러 시리즈라고 부르는 이런 함수 표현을 그 앞선 시대 사람이었던 오일러가 ... 그가 삼각함수를 심각하게 연구하고 발전시켰다는 점과 당시 이미 무한 수열의 합을 간단하게 나타내는 것이 뜨거운 문제 였다는 점에서 짐작은 할 수 있겠지만, 어떻게, 과연? 아직 구체적인 수학사적 사실은 발견 못했음. 궁금.
- ↑ 파이의 수열 표현을 참고하라.
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia








































