Pythagoras Th Proof Others
- 다른 증명들
쪼개기 방법이나 보태기 방법의 확장
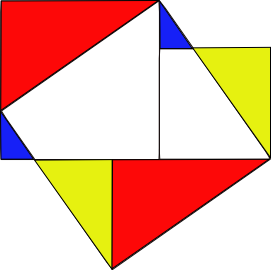
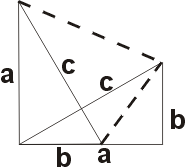
조각을 맞추는 것은 이미 했던 조각내어 비교하기 방법이나 보태어 비교하기와 크게 다르지는 않지만, 우리가 지금까지 해온 방법들은 직각삼각형에 '바깥쪽'으로 정사각형을 만들어 썼던 방법이다. '안쪽으로도' 집어 넣어 증명하는 예도 보기는 보았다. 이 경우는 바깥쪽으로 쌓은 정사각형을 해당하는 변에 대칭했던 것일 뿐이다. 우리의 기하학은 그것보다 훨씬 풍요롭다. 우리의 상상력도 그것에 갇혀있을 만큼 허약하지 않다. 더 많은 변환하여 조각을 비교해도 될 것이다. 아래 그림들을 보고 스스로 유추해보라.
- 위의 두번째 그림에서 AH 와 BC 가 수직이라는 것을 보여라. (헤론이 증명했다고 한다.)
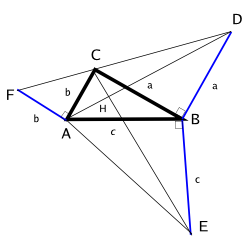
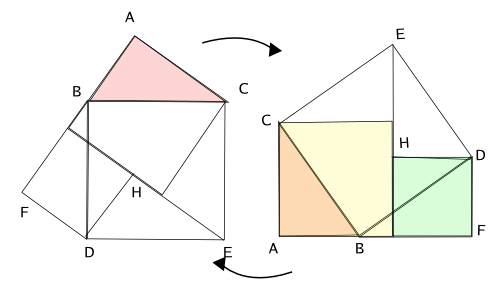
피타고라스 정리가 말하는 대로 습관적으로 직각삼각형의 변들로 이루어진 정사각형 꼴을 보아 왔다. 오른쪽의 그림은 사각형으로만 하던 우리의 증명 습관에서 볼 때 흥미로운 증명이다. 작도 방법은 다음과 같다.
- 꼭지점 B 에서 변 BC에 수직이고 길이가 BC인 선분을 작도한다.
- 꼭지점 B 에서 빗변 AC에 수직이고 길이가 AC인 선분을 작도한다.
- 꼭지점 A 에서 CA에 수직이고 길이가 CA 인 선분을 작도한다.
- 나머지는 그림처럼 잇는다.
어이지는 물음에 답하고 직접 증명해보라. 선분 FD는 꼭지점 C를 지날까? 직선 CE와 AD가 만나는 점은 어떤 성격을 가진 점일까? 직선 FB도 그 점에서 만난다고 할 수 있을까? 직선 FD와 CE의 관계는?
대수적 증명
큰 정사각형의 넓이 = 네개의 직각삼각형과 하나의 정사각형
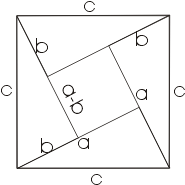
직각 삼각형의 세 변으로 큰 정사각형, 네 개의 같은 직각삼각형 그리고 한 개의 작은 정사각형을 다 다독거려 만들 수 있다. (옆의 그림) 작은 정사각형의 한변의 길이는 b-a 이다. 뻔하다. 그렇다면 넓이의 더하기 공리를 그대로 적용해서 대수적으로 풀어써보면,
여기엔 삼각형의 넓이나 사각형의 넓이를 대수적으로 나타낸 것, 그리고 넓이의 '더하기 공리'를 적용하여 대수적 식으로 나타낸 것, 그리고 마지막으로 그것에 대한 가장 간단한 계산 밖에 없다. 더할 수 없이 명쾌하고 간단하다. 이렇게 간단한 증명을 두고 왜 그 옛날 기라성같은 철학자 수학자들은 왜 그리 어렵게 증명했을까? 또 수천년 동안 왜 또 복잡한 증명을 시도하는 것일까? 그리고 이 증명은 정말로 그렇게 누구나 이해할 수 있는 쉬운 증명인가? 이것은 조각맞추기와 본질적으로 다른가 ?[1](생각해보고 토론해보라.)
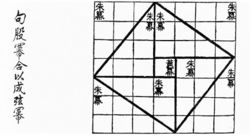
이 방법은 이미 고대 중국에서 서기 500년 쯤에는 이미 알려진 사실(오른쪽 그림)이었다. 서기 1200년 경 인도에서도 비슷한 방법을 썼다. [2] 이 도형은 이미 '쪼개어 비교하기' 방법에서 보았던 굿헤일의 증명에서도 비슷한 도형이 등장하였다..
삼각형을 이용한 증명
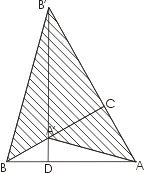
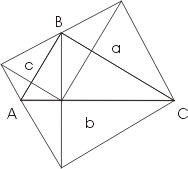
지금까지 피타고라스 정리를 증명할 때 우리는 습관적으로 직각삼각형의 변에 정사각형을 쌓았다. 안으로건 밖으로건. 물론 꼭 그래야 하는 것은 아니다. 우리에게 주어진 직각 삼각형에 보조선을 삼각형을 그어 쪼개고 보태보자.
- 직각삼각형 ABC를 꼭지점 C를 중심으로 90도 만큼 회전한다.
- 점 B'와 꼭지점 B 를 잇는다. 그렇게 얻어진 도형이 오른쪽 그림이다.
선분 B'A'를 연장해서 선분 AB와 만나는 점을 D라 하자. (D는 점 A와 B 사이에 있을까?) 그렇다면 B'D는 BAB'에서 밑변이 AB일 때 높이다. 이제 빗금친 부분의 넓이를 계산해보자. 큰 삼각형 BAB' 에서 BAA' 를 뺀 것과 같다. 왼쪽 등식은 그것을 말한다. 또는 쪼개진 두 직각삼각형 BCB' 와 ACA' 의 더하기이다. 오늘쪽 등식.
영국의 호킨스가 증명하였다. 1909년의 일이다.
벡터 개념을 써서
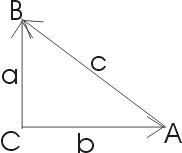
옆의 그림은 vector 의 개념을 쓴 것이다. vector에 대해서는 따로 설명할 것이다. 다만 몇가지 필요한 요점만 말해보기로 하자. 벡터란 방향이 있는 선분을 말한다. 새로운 수학적 개념인데, 기하학적 요소를 대수적으로 이해할 수 있고 응용력디 매우 큰 중요한 개념이다. 보통 그냥 선분은 a 로 쓴다면 그것에 해당하는 벡터는 로 쓴다. 새로운 수학적 대상의 연산을 정의해야 한다.
- 두 벡터 와 가 각 를 이룰 때, .
- 그래서 이고, 각 가 직각일 때, .
- 벡터의 곱은 교환, 결합, 분배 법칙이 모두 통한다.
- 벡터의 합은, 그림처럼 에서 로 간 것과 가 같은 점을 향할 때,
- 그리고 이는 과 다름이 아니다.
- 앞의 식에서 같은 벡터를 두번 곱하면 다.
- 옆의 그림처럼 직각삼각형인 경우 .
- 하지만 직각이 아닌 경우, 는 다. 이것은 피타고라스 정리를 일반화한 것과 같다.[3]
다른 것들
아휴 징그러.... 왜 이리 오래 걸리지... ? 며칠이 걸리는구만 이거 몇 쪽 쓰는데..
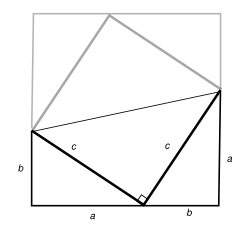
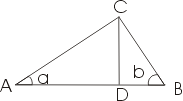
오른쪽 그림을 보면서 넓이에 대한 더하기 공리, 그리고 사다리꼴의 넓이를 나타내는 대수표현을 떠올리면 아래 식을 이해하는 것은 어렵지 않을 것이다.
Note
- ↑ 다음 연속그림은 조각 맞추기로 설명하고 있다.
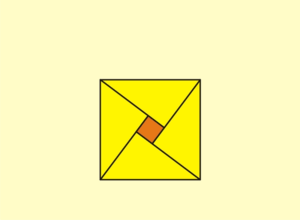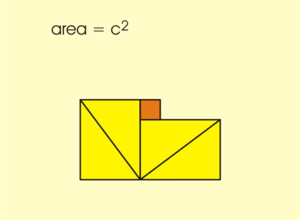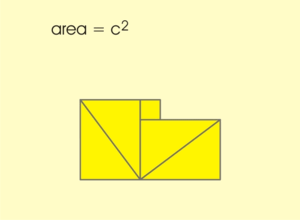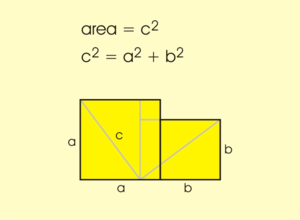
- ↑ 힌두교에서는 '천국의 계단' 은 중요한 개념이다. 이는 건축에도 광범위하게 반영되었다. 이것은 나중에... 헉.헉..
- ↑ 피타고라스 정리의 일반화에 대해서는 피타고라스 정리의 일반화 를 참조하세요~
Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia