Inversion Def Prop

Inversion & Inversive Geometry 로 돌아가기

정의와 기호  : Inversion 이란 어떤 연산인가?

기하에서 '뒤집기'의 가장 일반적인 정의는 아래와 같다. 어떤 점 O 와 상수 k 가 있을 때,

(정의) 아래 두 조건을 만족하도록 대응시키는 f 를 뒤집기(Inversion; 반전)라 부른다.

1. $OA\cdot Of(A)=k$
2. $f(A)\in OA$

이때 고정점 O 가 어떤 원 $\Sigma$ 의 중심이고 상수 k 가 그 원의 반지름의 제곱일 때가 여기서 보려고 하는 원에 대한 뒤집기'다.

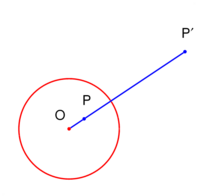
(정의) 위의 두 조건을 만족하고 O 가 어떤 원의 중심, k 가 그 원의 반지름의 제곱일 때 원 $\Sigma (O,r)$ 을 축으로 한 뒤집기 라고 한다.

어떤 도형 A를 뒤집기 한 결과를 편하게 쓰기 위해 A' 로 한다. 그리고 '대칭축'의 역할을 하는 원을 뒤집기 원이라 부르기로 한다.

위의 조건에 따르면 뒤집기는 유클리드 평면에서 평면으로의 변환(꼴바꿈)이었던 이동, 닮음, 아핀(affine) 변환들에 비해 '유클리드 평면의 변환'이 라고 할 수 없다. 거의 모든 점을 1: 1 대응시킬 뿐, 예외가 있기 때문이다. 다름 아닌 고정점 O는 대응시킬 수 없다. 뒤집기의 정의 때문에 비롯된 자연스러운 '예외' 항목이다. 그런데, 이 가정이 마음에 안들어 어쩌면 '뒤집기'를 아래와 같이 뒤집기 정의를 수정해보는 것은 어떨까?

뒤집기 원의 중심은 그 중심에 대응하고, 나머지 점들은 앞의 정의에 따라 대응하다.

만약 이렇게 정의하면 유클리드 평면 전체에 대해 1:1 대응이 되었지만, 새로운 문제가 생긴다. 연속성의 문제다. 뒤집기 원의 중심 근방 의 모든 점들은 중심 O 로부터 끝없이 멀리 떨어졌는데, O 는 다시 그 자리이기 때문이다. 이 문제를 다른 방식으로 해결할 것이다. 실수 공간에 허수(ideal number) 하나를 추가해서 복소수 공간으로 확장했듯이, 유클리드 평면에 한 점 (ideal point) 을 보태 평면의 개념을 확장하여 당면한 한계를 극복해 나갈 것이다.

실수 평면에서 좌표로 나타내면,

$(x,y)\rightarrow \left({\frac {kx}{x^{2}+y^{2}}},{\frac {ky}{x^{2}+y^{2}}}\right)$

이며, 복소 평면의 좌표로 나타내면

$z\rightarrow {\frac {k}{\bar {z}}}$

기호약속  : 어떤 점들의 집합 A 을 뒤집기 원 $\Sigma (O,r)$ 에 대해 뒤집어서 A' 로 대응한다면 아래 아래 세가지 방식은 모두 같은 말의 다른 표현들이다.

1. $\mathbf {I} _{O}^{r}(A)=A'$
2. $\mathbf {I} (O,r):A\rightarrow A'$
3. $A\xrightarrow {\Sigma (O,r)} A'$

만약 중심 O 나 반지름 r 중 특별히 밝히지 않아도 분명하거나 안써도 헷갈릴 것 같지 않으면 O 또는 r은 빼고 쓰겠다.

성질 : 뒤집기(Inversion)는 어떤 일을 할까?

어떤 문제를 던지고 풀어 기하적 성질들을 밝히는 방법은 꼭 하나여야 할 이유는 없다. 반대다. 하나의 문제를 푸는 방식은 무한개일 수 있다. 피타고라스 정리도 그랬거니와 다른 기하적 성질도 예외가 아니다. 좌표법이나 변환 같이 새로운 개념이 등장하여 수많은 문제를 푸는데 도움을 주기도 한다. 뒤집기의 응용 에서 보겠지만, 뒤집기도 마찬가지다. 먼저 뒤집기가 무엇을 어떻게 하는 연산인지 기본적인 성격을 보기로 하자

뒤집기의 뒤집기

가장 간단하지만 중요한 성질이다. 뒤집기 원에 대해 뒤집기한 것을 다시 뒤집으면 그대로다. 정의에서 k는 상수이므로 분명한 성질이다.

뒤집기 원에 대해 뒤집힌 점들의 집합을 그 원에 대해 다시 뒤집으면 본래 집합이다.  : $\mathbf {I} (\mathbf {I} (A))=A$

그래서, 어떤 뒤집기 원에 대해 역뒤집기(또는 뒤집기의 역연산)과 뒤집기는 같다.: $\mathbf {I} ^{-}=\mathbf {I}$

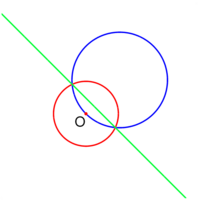
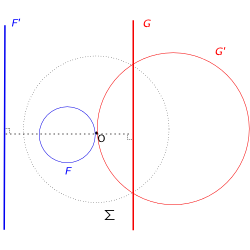
오른쪽 그림에서 볼 수 있듯, 녹색 선이 '거대한' 뒤집기 원의 한 부분이라면, 빨간색 원을 뒤집으면 파란색 원이 되고 뒤집힌 파란색 원을 뒤집으면 빨간색 원이 된다. 이런 성질을 가진 연산들을 'involution' 이라고 부른다. 지금까지 우리가 본 기하적 연산 중에는 대칭들이 있었다. 뒤집기와 대칭의 첫번째 같은 성질  !

뒤집기 원의 안과 밖

어떤 세상을 다른 세상으로 대응시키는 축으로 우리는 원을 전제로 하고 있다. 점 A 가 중심 뒤집기 원의 중심 O 로 부터 반지름 만큼 떨어져 있다면 그 점은 바로 그 점으로 대응할 것이다. 따라서 뒤집기 원의 경계에 있는 모든 점은 그 자신으로 대응한다.

원의 점을 그 자신에 대해 뒤집기 하면 그 점이다. : $\forall A\in \Sigma (O,r)\ (\ \mathbf {I} _{O}^{r}(A)=A\ )$

뒤집기 원에 있지 않은 점들은 어떻게 될까? 뒤집기 원이 아닌 모든 점들은 크게 보아 원 안의 점과 원 밖의 점으로 나눠 생각해 볼 수 있다. 이 때, 뒤집기의 정의로부터 아래의 사실은 분명하다.

원의 '안쪽' 에 있는 점은 '바깥쪽' 점에 대응한다.  : $\forall \Sigma \forall A\ (A\in \mathbf {int} \Sigma \Rightarrow \mathbf {I} (A)\in \mathbf {ext} \Sigma \ )$

뒤집기의 뒤집기는 바로 원래와 같으니, 바깥쪽 점을 뒤집으면 안쪽으로 대응할 것이다. 이것도 어떻게 옮길까? 에서 본 대칭의 개념과 비슷하다. '대칭'이 직선으로 나뉜 두 반평면은 한쪽에서 다른 한쪽으로 대응했듯, '뒤집기'는 원으로 나뉜 두 '반평면'이 한쪽에서 다른 한쪽으로 대응한다. 원의 점들이 그 자신으로 대응하는 것도 마찬가지다. 따라서 (대칭:직선) 과 (뒤집기:원) 은 비슷하다.

아무리 작은 원을 뒤집기 원으로 잡아도 그 바깥의 모든 세상을 원 안으로 옮길 수 있다. 물론 모양은 많이 달라질 테지만, 어떤 성질들은 변하고 어떤 성질들은 안변한다. 변하지 않은 성질은 '기하학적으로 보다 근본적인 어떤 성질'이라고 볼 수 있다.

뒤집기의 성질을 보는데 기초적인 역할을 하는, 간단하지만, 매우 중요한 성질 부터 확인하고 이야기를 더 풀어가기로 하자.

다른 두 점 A, B 를 뒤집어서 A', B' 가 된다면, 삼각형 OAB 는 OB'A' 와 닮았다.  : $OAB\simeq OB'A'$

뒤집기한 결과이므로 다음의 관계가 성립할 수 밖에 없다.

$OA\cdot OA'=r^{2}=OB\cdot OB'$ 다. 따라서, $OA:OB=OB':OA'$

이 식은 우리에게 무엇을 말하고 있나? 그렇다. "두 삼각형은 닮은거야" 라고 속삭이고 있다. 다만,

$\angle OAB=\angle OB'A'\ ,\ \angle OBA=\angle OA'B'$

직선 뒤집기

직선을 보자. 어떻게 바뀔까? 직선도 두 경우로 나뉜다. 중심 O 를 지나는 직선과 그렇지 않은 직선으로. 뒤집기 원의 중심 O를 지나는 직선을 뒤집으면 점의 위치는 바뀔것이다. 원 안의 점들은 밖으로 밖의 점들은 모두 안으로. 하지만, 그 직선에서 원의 중심 O 과 교차하는 점 빼고는 그대로 남는다. 한 점을 건너뛴 직선이란 집합 (두 반직선?) 자체는 그 자신으로 남는 것이다.

어떤 뒤집기 원의 중심 O을 지나는 직선을 뒤집기하면 바로 그 직선이다.

$\forall \Sigma _{O}^{r}\forall l\ (O\in l\ \rightarrow \ \mathbf {I} (l)=l\ )$

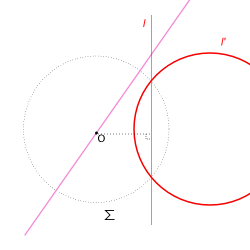
그렇다면 중심 O 을 지나지 않은 직선들은 ? 직선은 두 점으로 정해지므로 두 점 A, B 을 생각해보자. 한 점 A 은 원의 중심으로부터 직각을 이루게 잡자. 다른 점 B 은 그렇지 않을 것이다. 이제 직선을 규정했던 점들을 뒤집어 A', B' 를 보자. 이 점들은 어떤 원의 점들이다. 이것은 아래 사실을 확인하여 이해할 수 있다.

삼각형 OA'B'는 OA' 가 빗변이고 각 OB'A'는 직각인 직각삼각형이다.

점 A 를 고정하고 그 직선의 B 대신 어떤 다른 점 X 을 잡더라도 이런 성질은 성립한다. 그런 점들의 집합은 그래서 OA'를 지름으로 하는 원을 뜻한다. 확인해보자.

직각 삼각형 OAB 와 새로 얻은 두 점으로 이룬 OA'B'는 어떤 관계일까? 앞의 두 점을 뒤집었을 때 원의 중심과 이루는 삼각형의 닮음에서 보았듯이 각 OAB이 각 OB'A' 과 같은 닮은 삼각형이다. 따라서, 따라서 OB'A' 는 직각이고, OA' 가 지름을 이루므로 원은 뒤집기 축의 중심 O 을 지날 원이다.( 직선의 어떤 점이 O 로 대응하겠는가? )

어떤 뒤집기 원의 중심 O을 지나지 않는 직선을 뒤집기하면 중심 O 을 지나는 원이다.

$\forall \Sigma _{O}^{r}\forall l\ \exists \sigma \ (O\notin l\ \rightarrow \ \mathbf {I} (l)=\sigma \ \And O\in \sigma \ )$

지금까지 이동, 닮음, 아핀(Affine) 변환에서는 어떤 경우도 직선은 직선으로 원은 원으로 바뀌었다. 그런데, 이 경우 직선의 점들은 드디어 직선성(collinear)이 깨진다. 그렇다고 마냥 무질서해지는 것은 아니다. 원을 이룬다(concyclic). 좁게 보면 직선성이 깨지지만, 넓게 보면(직선이 원의 특수한 경우라 볼 경우) 깨지지 않는다고 볼 수 있다.

다른 주제로 넘어가기 전에 조금만 더 캐보자.

• 위에서 뒤집기 원과 뒤집을 직선이 두 점 X, Y 에서 만난다면 '뒤집힌' 원은 중심 O 을 지나고 X, Y 도 지난다.
• 이 중심 O에서 뒤집힌 원의 접선은 뒤집힐 직선과 평행하다. (아래 각도 변하지 않음에서 중요한 역할을 한다.)
• A'B' 의 길이는 물론 뒤집기 원이 품고 있는 정보와 대응할 두 점 A, B 일 것이다. 어떤 식을 가질까?

$OA:OB=OB':OA'=AB:B'A'$

따라서 선분 A'B' 의 길이는

${\frac {AB\cdot OB'}{OA}}={\frac {AB\cdot r^{2}}{OA\cdot OB}}$

• 직선이 뒤집혀 대응된 원의 중심은? 마찬가지로 O 와 주어진 직선 l 로 결정될 것이다. 그 중심은 $\mathbf {I} _{O}(S_{l}(O))$ 다! $S_{l}(O)$ 는 축 l 에 대한 대칭을 뜻한다. 따라서 뒤집기 원의 중심을 그 직선에 대칭한 점은 뒤집기 할 원의 중심을 뒤집은 것과 같다.

원 뒤집기

뒤집기 원과 다른 원도 크게 보면 두 경우가 있다. 뒤집기 원의 중심을 지나는 원과 그렇지 않은 원이다. 뒤집기 원의 중심을 지나는 원은 간단하다. 뒤집기의 뒤집기는 그 자신으로 대응하므로 중심을 지나지 않은 직선을 뒤집은 것이다. 이때,

뒤집기 원의 중심 O 을 지나는 원을 뒤집으면 점 O를 지나지 않는 직선이 된다.

$\forall \Sigma _{O}^{r}\forall \sigma \ \exists l\ (O\in \Sigma \ \rightarrow \ \mathbf {I} (\sigma )=l\ \And O\notin l\ )$

이 원의 중심을 지나는 직선과 만나는 점 O, A는 직선의 어디와 만날까? A' 는 정의에 따라 반직선 [O,A) 에 있어야 하고, 동시에 뒤집힌 직선을 지나야 하므로, 직선 OA와 수직인 점이다. 따라서 뒤집힌 원과 지름을 이루는 직선이 만나는 다른 점 - 여기서는 점 O - 에서 접선은 뒤집힌 직선과 평행하다.

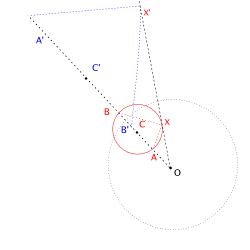
이제 남은 것은 원의 중심을 지나지 않는 다른 원들이다. 어떻게 될까? 원을 결정하는 것은 중심과 반지름이므로 그것으로부터 시작하자. 뒤집기 원의 중심 O 과 뒤집을 원의 중심 C 을 지나는 직선이 있을 것이다. 그렇다면 뒤집힌 원의 중심 C'는 물론 반직선 [OC) 에 있다. O, C, C'이 놓인 직선이 있을 것이고, 그 직선과 만나는 점들은 지름을 이룬다. 뒤집힐 원과 만나는 점을 A, B 라 하자. 이 두 점은 뒤집힐 원의 지름을 이룬다. 그 점의 뒤집힌 점 A'와 B' 도 그 직선에 있다. 이제 아무 점 이나 제 3 의 점 X를 잡으면 각 AXB 는 직각일 것이다. 그리고 닮음에 따라

$\angle OXB=\angle OB'X'\ ,\ \angle OXA=\angle OA'X'$

라서,

$\angle A'X'B'=\angle OB'X'-\angle OA'X'=\angle OBX-\angle OAX=\angle AXB$

이므로 각 A'X'B'도 직각을 이룬다. 따라서 점 X를 고를 때, 아무 점 이나 잡았으므로 두 점 A', B' 가 이름을 이루는 뒤집힌 도형은 원이 될 수 있다. (과연 진짜 원이 될 수 있을까? 혹시 원의 일부분만 되는 것은 아닐까? (또는 뒤집어서 원이 되는 것은 원밖에 없을까? 혹시 다른 도형을 뒤집어서 원이 될 수도 있지 않을까?))

뒤집기 원의 중심 O을 지나지 않는 원을 뒤집기하면, 중심 O 을 지나지 않는 원이다.

$\forall \Sigma _{O}^{r}\forall \sigma \exists \sigma '\ (O\notin \sigma \ \rightarrow \ \mathbf {I} (\sigma )=\sigma '\ \And O\notin \Sigma )$

뒤집힌 원은 어떤 성격을 가질까? 지금까지의 사실로만 봐도 다음 사실은 명확하다.

뒤집기 원과 뒤집힐 원이 만나는 점은 뒤집힌 원에도 있다.

이렇게 분명한 사실 말고 뒤집힐 원과 뒤집힌 두 원, 또는 뒤집기 원들의 관계를 더 자세히 밝혀볼 수 없을까? 옆의 그림을 보자. 어떤 두 원 $\sigma (C,r_{1}),\sigma (C',r_{2})$ 이 하나에서 다른 하나로 뒤집히는 관계일 때, 이 원들은 뒤집기 원 $\Sigma (O,r)$ 과 아래의 관계를 갖는다. '방향'에 주의 !

중심 O 에서 직선을 그어 $\sigma (C,r_{1})$ 과 만나 두 점을 X, Y 라 하고 $\sigma (C',r_{2})$ 과 만나는 점을 Y', X' 라 하면, $OX=k\cdot OY',\ OY=k\cdot OX'$ 인 상수 k 가 있다. 이런 관계에 있는 도형들을 homothetic 관계라 한다. 따라서,

뒤집힐 원과 뒤집힌 원의 관계는 뒤집기 원 O 에 homothetic 관계다.

뒤집기 원의 중심을 지나지 않은 원도 두 종류로 분류해볼 수 있다 : 하나는 뒤집기 원의 중심을 자기의 중심으로 하는 원, 다른 하나는 그렇지 않은 원. 너무 막연한 원은 두고 더 분명한 원, 다시말해, 뒤집기 원과 동심원 관계인 원을 보자. 그런 원에 대해서는 아래 사실을 뽑아낼 수 있다. (왜 그럴까?)

뒤집기 원의 중심이 O 고 반지름이 r 이라 하자. 뒤집힐 원은 중심이 O 고 반지름이 c 라 하자. 이 원을 뒤집으면 중심이 O 고 반지름이 ${\frac {c}{r^{2}}}$ 인 원이다.

혹시 뒤집힐 원의 중심이 뒤집힌 원의 중심으로 대응하지는 아닐까? C와 C'가 한 반직선에 있다는 것은 분명하다. 그렇다면 $OC\cdot OC'=r^{2}$ 일까? 결코 그렇게 될 수 없다. 뒤집히는 원의 지름을 이루는 A, O, B 를 보면, AO 의 길이와 OB 의 길이가 뒤집기 원의 위치에 따라 '더 쭉쭉' 늘어나는 쪽과 덜 늘어나는 쪽으로 나뉘니까, 뒤집힌 세 점 A', O', B' 에서 B'O' 와 O'A' 가 길이가 같아질 수 없기 때문이다. 또는 A'B' 의 길이를 AB, OA, OB, r 로 나타낸 앞의 식으로 밝힐 수도 있다.

당연한 결과이지만, 우리의 '자연스러운 기대'를 어긋나서 별로 마음에 안든다. 하지만, 이런 불편한 마음은 만나는 점에서 '각은 변하지 않는다'는 사실을 깨닫게 되면 위안을 받을 수 있다. 점 뒤집힐 원의 지름을 이루는 점 A에서 접선은 뒤집힌 다음에도, 평행으로, 같은 각을 유지한다.

원의 기초적인 성질 중 우리에게 도움을 줄 만한 것 하나. 어떤 점 P 을 지나는 직선 l이 어떤 원을 두 점 X,X' 을 지나고 점 P 을 지나는 다른 직선이 원과 Y, Y' 에서 만나면, 항상 $PX\cdot PX'=PY\cdot PY'$ 이므로,

어떤 원의 한 점이 뒤집힌 뒤에도 그 원에 있으면 원의 모든 점은 그 원에 남는다

$\forall X,Y\in \sigma \ (X'=X\rightarrow Y'=Y)$

두 원의 뒤집기 : 만남(concurrent), 벌어진 정도(angle)는 변하지 않는다.

이제 관심을 두 직선이나 두 원을 넓혀가보면서 뒤집기의 행동양식을 파악해보자. 물론(?), 관심은 원들의 관계에 집중한다. 가장 기초적인 성질인 만남의 성질(concurrent) 부터 보자. 두 도형의 만나는 점은 뒤집힌 다음에도 만날까? 물론이다. 어떤 점 P 가 도형 F에 속한다면 그 점은 뒤집힌 다음 P에 대응하는 점 P'는 F' 에 있을 것이고 이것은 다른 도형 G에 대해서도 마찬가지다. 만나는 점 P는 두 두형 F 와 G 에 대해 $P\in G$ 이고 $P\in G$ 다. 또 $P\in F\ \Rightarrow \ P'\in F'$ 이고 $P\in G\ \Rightarrow \ P'\in G'$ 이므로,$P'\in F$ 이고 $P'\in F'$. 간단히 쓰면 $\forall F,G\ \forall P\ (\ P\in F\cap G\ \rightarrow \ P'\in F'\cap G'\ )$ 이다. 따라서 , 만나는 점이 뒤집기 원의 중심 O 가 아니라고 가정하면,

어떤 두 도형 F, G 이 만나는 점은 뒤집힌 F', G' 에서도 만난다.

그 역도 성립하므로, 만나는 점의 개수는 변하지 않는다. 이제 구체적인 경우로 들어가보자. 두 원의 위치 관계는 세 경우다. 만나지 않거나, 한 점에서 만나거나, 두 점에서 만나는 경우다. 보다 명확한 경우부터 보자.

먼저 한 점에서 만나는 경우. 다시 말해 두 원은 접한다. 그 점이 뒤집기 원의 중심 O 에서 접하거나 다른 점에서 접할 때. 중심 O 에서만 접한다면 두 원 모두 직선이 되고 다른 어떤 점에서도 만나지 않는다. 따라서 뒤집힌 결과인 두 직선은 평행하다. 아직 우리에게는 점 O 를 뒤집을 권리가 없기 때문에 어쩔 수 없다.

뒤집기 원의 중심 O 에서만 만나는 어떤 두 원을 뒤집으면 평행한 두 직선이 된다.

이제 만나는 점이 O 가 아닌 경우. 이때도 앞에서 본 것 처럼 두 원은 모두 어떤 원으로 바뀌고 한 점에서만 만난다. 따라서 접한 점은 뒤집히고 나서도 그대로 접하게 된다. 하지만, 상상해보자. 그 만나는 점이 점점 중심 O 의 근방에 가까이 오고 있다고. 가까이 올 수록 두 원이 뒤집히면 반지름은 점점 커지고, 만나는 점은 중심 O 에서 점점 멀어지게 된다. 하지만 아무리 멀어져도 만나는 점이 O 가 되지 않는 이상 한 점에서 만나는 것은 분명하다. 그런데 점 O 에서 접하는 순간, 두 직선은 마침내 평행한 직선이 되고 만나는 점이 사라진다 ! 이것은 상당히 우리 영혼의 평온을 뒤흔들게 한다. '뒤집기'가 더 그럴싸 해지고 우리의 상상에 일관성 있게 하려면, 결국 이 평행한 두 직선도 어디선가 만나면 좋을 것이다. (물론 이것이 더 우리는 괴롭힌다고 주장할 수도 있다. 그것의 직관과 어긋나기 때문이다. 하지만 그것은 습관이 만든 직관과 어긋날 뿐이다.) 그래서 그런 점 ideal point 을 보태 두 점이 만나도록 한다. 그런 두 원은 두 평행한 직선으로 바뀔 것이기 때문에 평행한 직선은 어떤 것이든 ideal point 에서 만난다. 이 사실만 봐도 새로운 한 점이 보태지면서 유클리드 기하와 얼마나 다르게 되는지 짐작할 수 있을 것이다. 이에 대해서는 더 자세히 볼 것이다. 일단 지금 우리의 주제에서 너무 벗어나지는 말자.

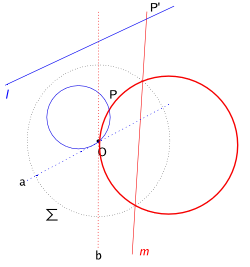
두 점에서 만나는 경우. 그 두 점 중 하나가 중심 O 를 지날 때와 그렇지 않을 경우로 다시 나뉜다. 뒤집기 원의 중심 O 에서 만난다면? 우선 두 원은 직선 l, m 으로 대응할 것이다. 두 원에서 만나는 다른 점 P 은 뒤집혀 P' 이 되더라도 두 직선에서 만난다. 따라서,

뒤집기 원의 중심 O 와 다른 점 P 만나는 두 원을 뒤집으면 점 P 에서 만나는 두 직선이 된다.

물론 이 경우도 앞에서 했던 것 처럼 P 가 점점 O 의 근방으로 다가오는 경우를 상상해볼 수 있다. 남은 경우에 대해서는 아직 뭐라고 할말이 없다. 만나는 두 점은 뒤집혀도 두 점에서 만난다는 말밖에는. 그런데 과연 '만남' 자체 말고 어떤 성질이 유지되는 것일까?

이야기를 더 뽑아나가기 위해 원에서의 각을 정의해보자. 원의 점 P 에서의 기울기는 그 점에서 접선으로 결정한다. 따라서 어떤 점 P 에서 두 원이 만났다면 두 원의 각은 그 점에서 접선의 각이라고 정의한다. 뒤집기는 직선이 원으로 바뀌고 위치나 크기도 크게 바뀌고 그것을 측정하기도 쉽지 않았다. 언뜻 눈으로봐서는 많은 것을 바꾸는 것처럼 보인다. 하지만, 넓은 의미에서 collinear 성질이 안바뀌고, concurrent 성질도 바뀌지 않았다. 또하나 매우 중요한 성질도 바뀌지 않는다. 만나는 점에서 두 원이 이루는 각도 변하지 않는다.

두 원(또는 두 직선)이 이루는 각은 뒤집어도 변하지 않는다.

어떤 두 점 P', Q' 에서 만나는 원이 있다고 하자. 만나는 한 점 P 에서 접선 l, m 각의 기울기를 $\theta$ 라고 하자. 그 접선들을 뒤집으면 중심 O 를 지나는 원들일 것이다. 직선들이 P' 에서 만나니 두 원은 또 다른 한 점 P 에서 만나고 $\mathbf {I} _{O}(P)=P'$ 다. 중심 O에서 뒤집힌 원의 접선은 뒤집힐 직선과 평행하다. 고 하였으므로, 한 원$\alpha$ 에서 점 O 를 지나는 접선 l 은 직선 a 와 평행하다. 다른 원의 접선 m 은 b 와 평행할 것이다. 그래서 점 O 에서 접선들의 각도 $\theta$ 다. 또, 두 원의 중심을 잇는 직선에 만나는 점들은 대칭이므로, 만나는 두 점에서는 각이 같을 수 밖에 없다. 따라서 O 에서 접선들의 각은 P' 에서 접선들의 각과도 같다. 따라서 P 에서의 각은 P' 에서의 각도 같다.

Q. 마지막 남은 경우 P 나 Q 점 중 하나가 점 O 를 지나는 경우에 대해서 스스로 생각해보라.

따라서, 두 원이 직각을 이룬다면 그 원들이 뒤집힌 결과인 두 원도 직각을 이룬다. 도형의 성질 중 중요한 요소인 '직각성'도 변하지 않는 것이다 ! 그렇다면 직각이 아닌 원 중에서 뒤집어서 직각인 원이 되는 어떤 원이 과연 있을까? 직각성과 관련된 내용은 Inversive Geometry 에서 더 자세히 보기로하고 결론만 여기서 말하고 넘어가자. "없다."

이제 우리는 수많은 기하 문제를 뒤집기의 도움을 받아 풀 수 있는 준비가 '거의' 되었다. 점 O 를 뒤집는 점을 추가하여 직선과 원의 경계를 허무는 새로운 기하학에 대해서 먼저 알아보고 응용으로 넘어가기로 하자.

Note

Math : Math글쓰기 | Math번역 | MathBoard | Math&Culture | MathMoim
OnLineMathCenter | MathCamp | SoftMathJournal | MathBook | CyberAcademia | Academia